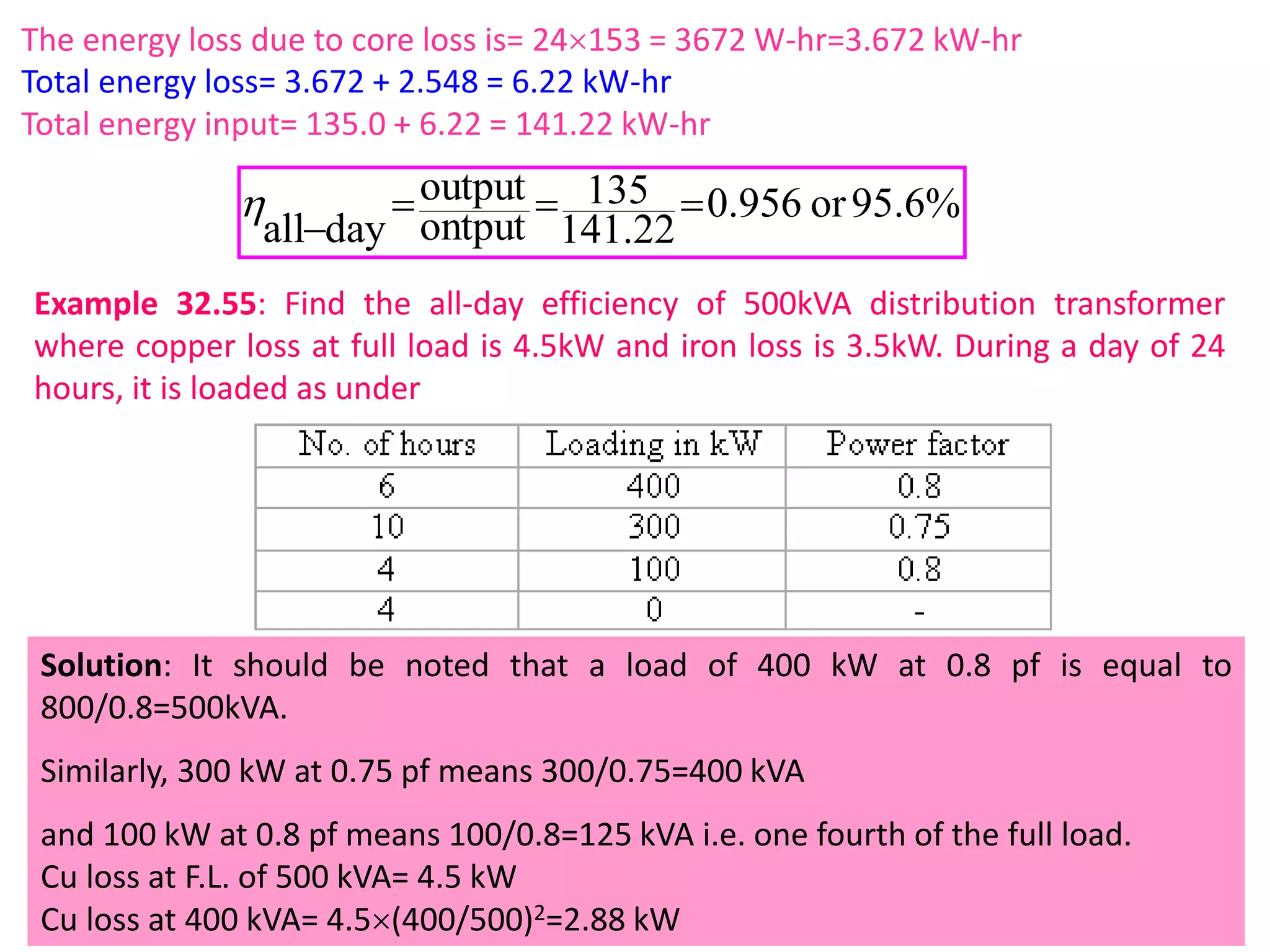
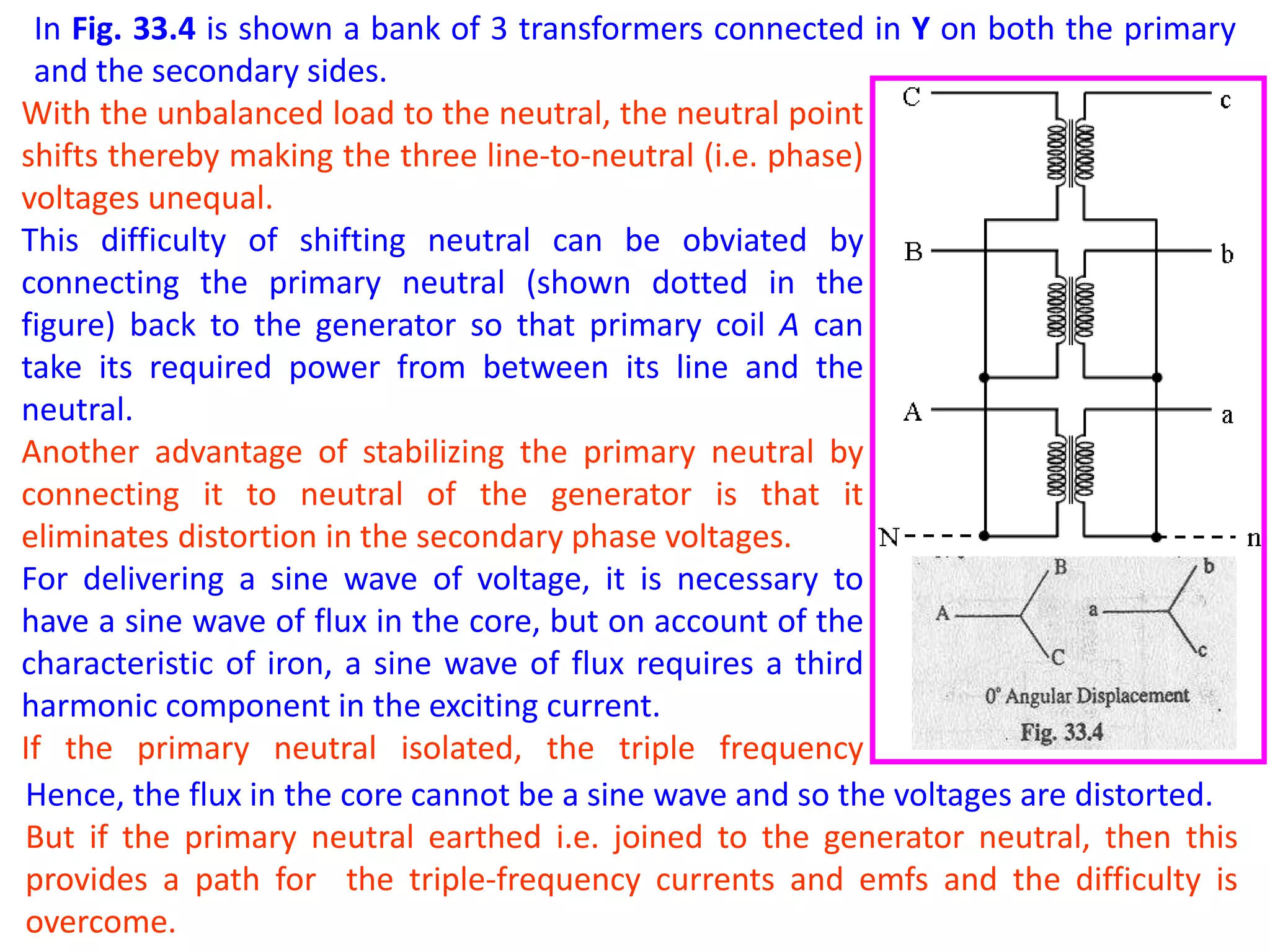
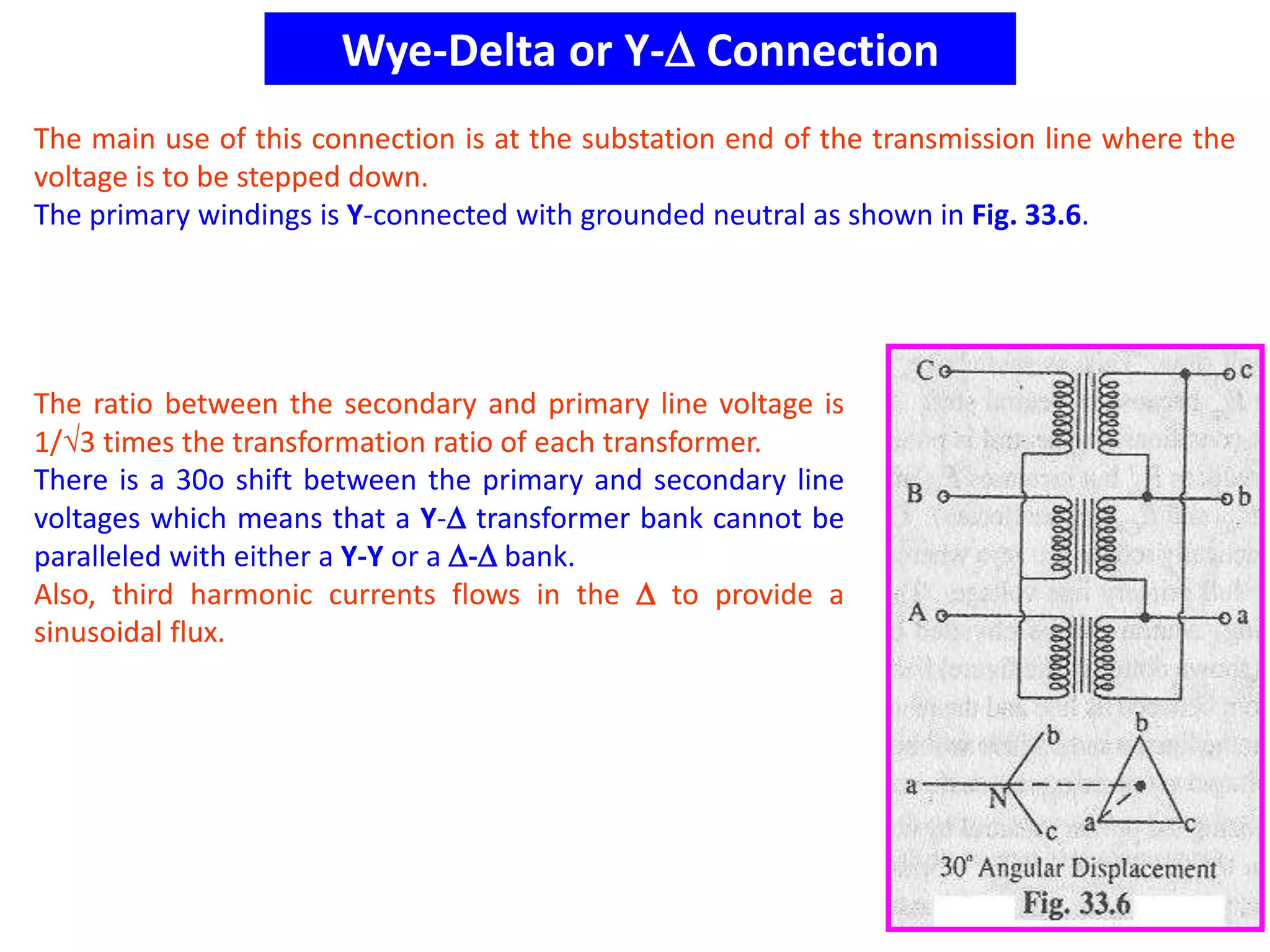
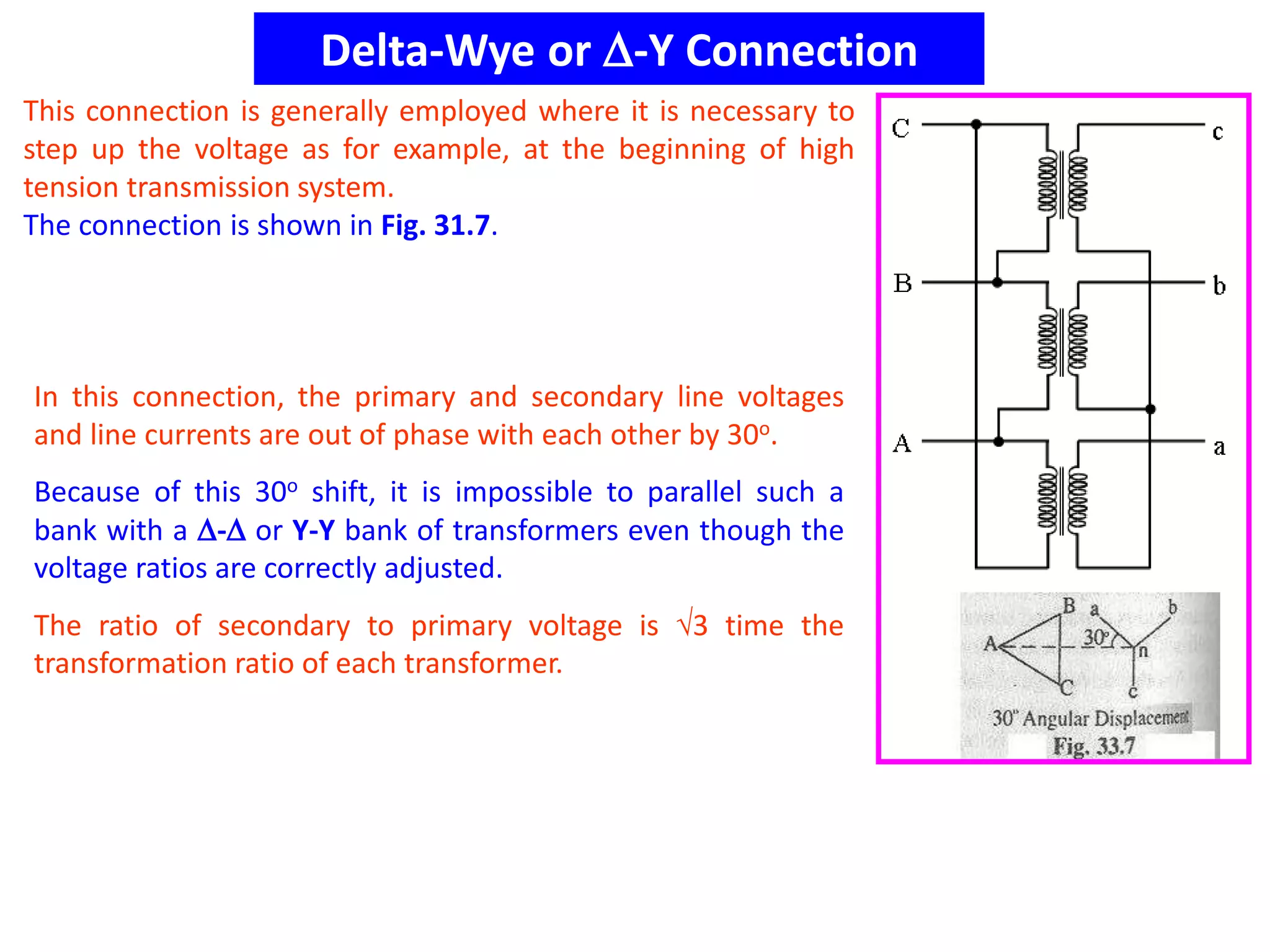
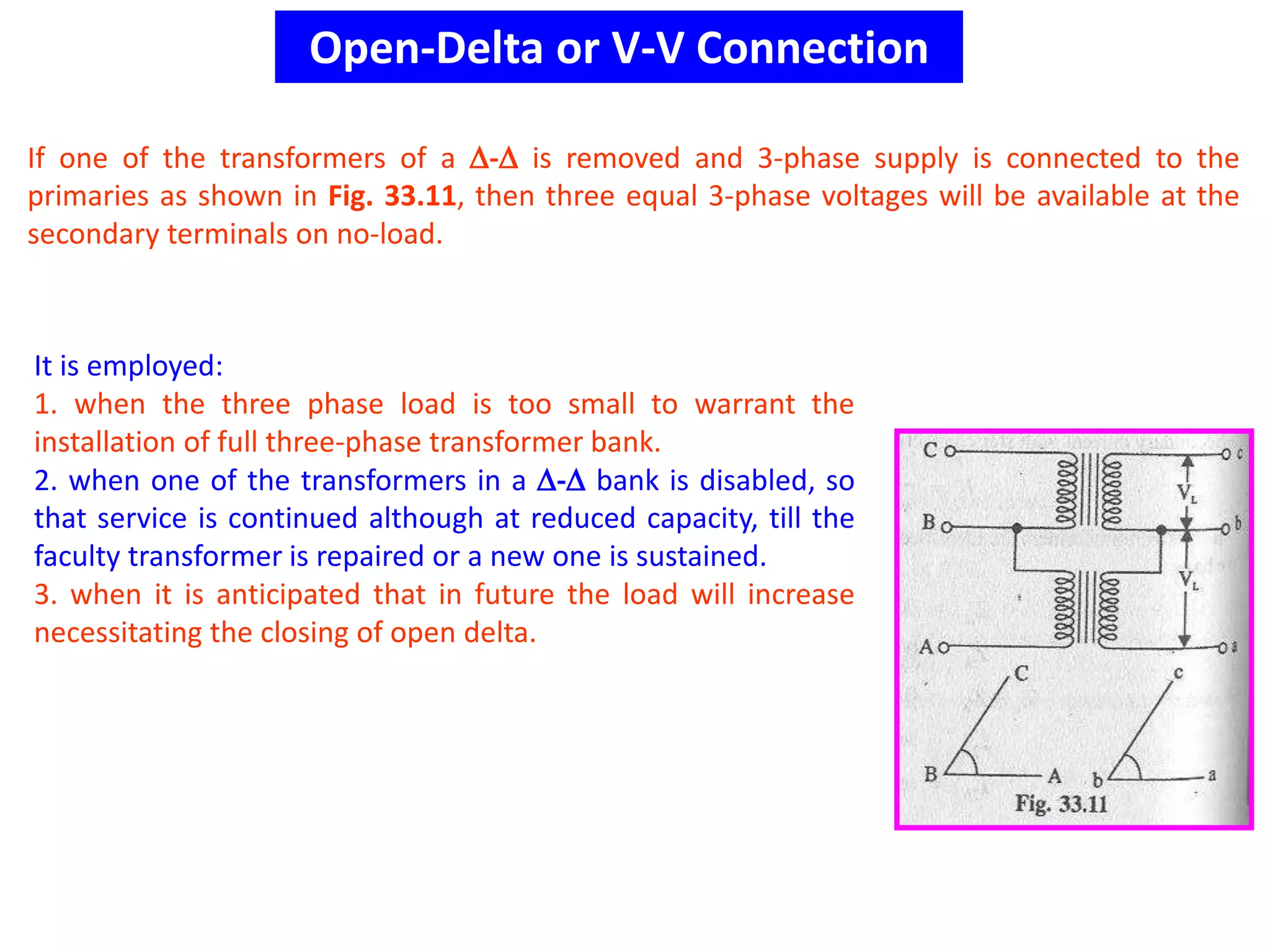
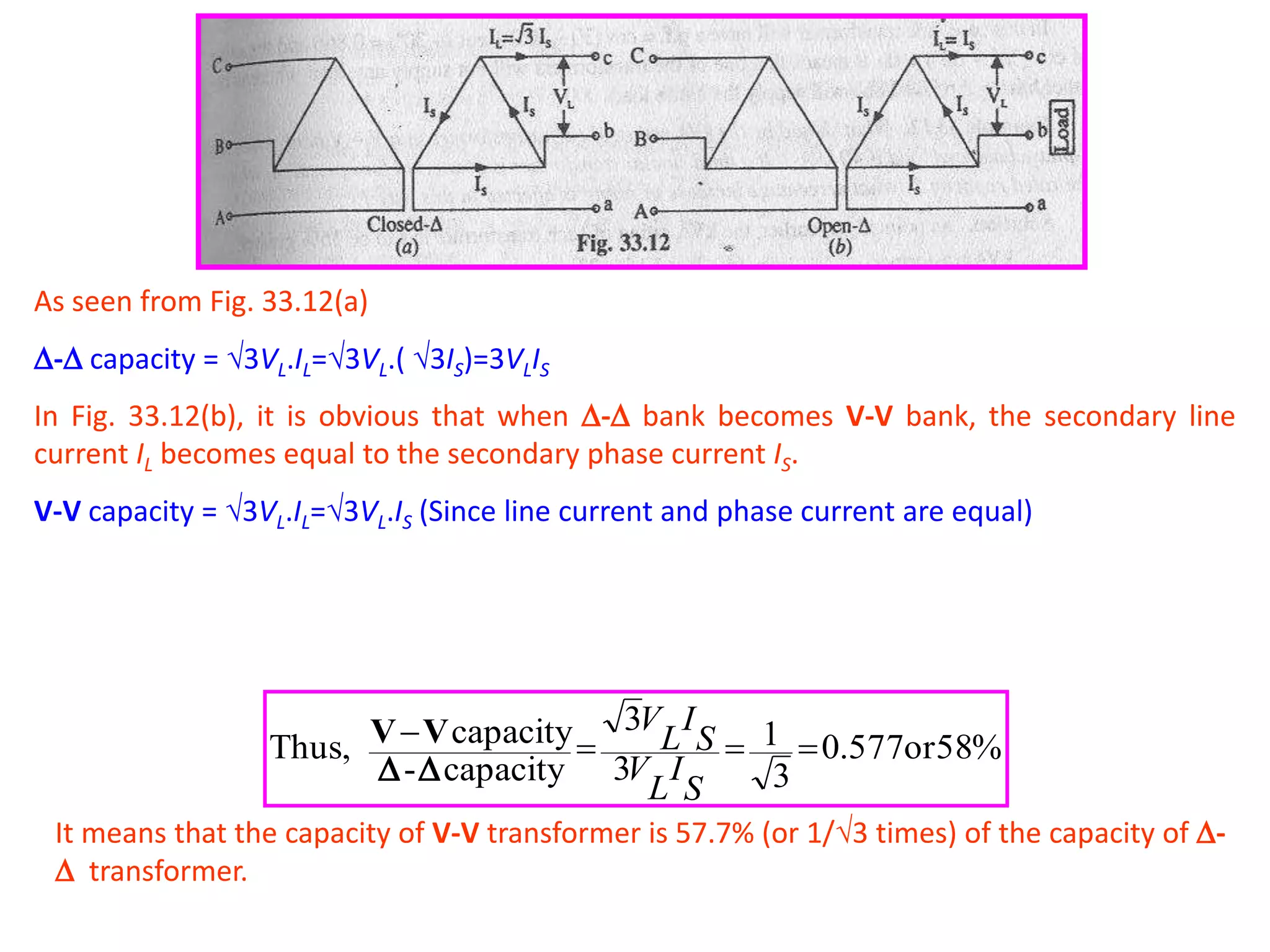
This document discusses transformer ratings, regulation, losses, and efficiency. It provides explanations for the following key points: 1. Transformer ratings are in kVA rather than kW because total transformer loss depends on volt-ampere (VA) and is independent of load power factor. 2. Regulation is defined as the percentage difference between no-load and full-load secondary terminal voltages, with regulation down using no-load voltage and regulation up using full-load voltage. 3. The main losses in transformers are core/iron loss and copper loss. Core loss is constant with load while copper loss depends on load and increases with higher load. 4. Efficiency is calculated based on output versus input power

1. Why Transformer Rating in kVA?
As seen, Cu loss of transformer depends on current and iron loss on voltage.
Hence, total transformer loss depends on volt-ampere (VA) and not on phase
angle between voltage and current i.e. it is independent of load power factor.
This is why rating of transformers is in kVA and not in kW.

2. Regulation of a Transformer Or Transformer Regulation
Regulation of a transformer is defined as the difference between the full-load and
no-load secondary terminal voltages expressed as a percentage of the full-load
voltage.
When a transformer is loaded with a constant primary voltage, the secondary
voltage decreases because of its internal resistance and leakage reactance.
Let, 0V2 = secondary terminal voltage at no-load
= E2 = E1K=KV1 because at no-load the impedance drop is negligible.
V2 = secondary terminal voltage on full load

3. The change in secondary terminal voltage from no-load to full load is=0V2-V2.
This change divided by 0V2 is known as regulation ‘down’.
If this change is divided by V2 i.e. full-load secondary terminal voltage, then it is called
regulation ‘up’.
100
2
220uregulation%and
100
20
220downregulation%






V
VV
p
V
VV
Regulation is usually to be taken as regulation ‘down’.
The lesser this value, the better the transformer, because a good transformer should be
kept secondary terminal voltage as constant as possible under all conditions of load.

4. Losses in Transformer
Since a transformer is a static device, there are no friction and windage losses.
Hence, the only losses occurring are:
(a) Core or Iron Loss
(b) Copper Loss
Core or Iron Loss
It includes both hysteresis loss and eddy current loss.
Because the core flux in transformer remains practically constant for all loads the
core loss is practically the same at all loads.
Hysteresis loss: Wh=Bmax
1.6fV watt; Eddy current loss: We=PBmax
2f2t2 watt
Where, V=volume of the core in m3; =Steinmetz hysteresis coefficient;
t=thikness.
These losses are minimized by using steel of high silicon content for the core and
by using very thin laminations.
Iron or core loss is found from the O.C. test.
The input of the transformer when on no-load measures the core loss.

5. Copper Loss
This loss is due to the ohmic resistance of the transformer windings.
Total Cu loss=I1
2R1+I2
2R2= I1
2R01=I2
2R02.
It is clear that Cu loss is proportional to (current)2 or kVA2.
So, Cu loss at half-load is one-fourth [(1/2)2=1/4] of that at full load.
Cu loss at one-quarter-load is one-sixteen [(1/4)2=1/16] of that at full load.
Cu loss at five-fourths -load is twenty five by-sixteen [(5/4)2=25/16] of that at full load.
The value of copper loss is found from the short-circuit test.

6. Efficiency of a Transformer
The efficiency of a transformer at a particular load and power factor is defined as the output
divided by the input- the two being measured in the same unit (either watts or kilowatts).
Thus the equation of efficiency can be written as:
input
outputEfficiency
LossIronLossCuoutput
output
lossesoutput
outputEfficiency




We can write the efficiency equation in terms of output and losses as:
input
Losses1
input
losses-input,Efficiency 
Efficiency can be computed by determining core loss from no-load or open circuit test and
Cu loss from the short-circuit test.
Also, the efficiency equation in terms of input and losses can be written as:

7. Condition for Maximum Efficiency
cuWRIRI 
02
2
2
or
01
2
1
lossCu
Iron loss= hysteresis loss+ eddy current loss=
Wh+We=Wi
1
cos
11
01
2
11
1
cos
11
01
2
11
cos
11
1
cos
11
losses
1
cos
11









IV
i
WRI
IV
i
WRIIV
IV
IV

1
cos
111
cos
11
01
2
11




IV
i
W
IV
RI

Differentiating both sides with respect to I1, we get
1
cos2
111
cos
1
01
1 



IV
i
W
V
R
dI
d hence,0
1
,efficiencymaximumFor 
dI
d
LossIronLossCu  means,That
02
2
2
or
01
2
1
RI
i
WRI
i
W
The output current corresponding to maximum efficiency is:
Considering primary side, Primary input, =V1I1cos1
02
/
2
R
i
WI 
By proper design, it is possible to make the maximum efficiency occur at any
desired load.

8. All-Day Efficiency
Transformers are frequently provide service 24 hours per day, although the load is by no
means constant over this entire period.
Under such conditions, the transformer must be judges by its all day efficiency rather than by
its full-load efficiency.
All day efficiency (also known as ‘operational efficiency’ or ‘energy efficiency’) is a ratio of
energy output to energy input taken over a 24-hr period.
Mathematically, the expression of all-day efficiency can be written as follows:
)hours24for(
kWhininput
kWhinoutput
dayall



To find this all-day efficiency, we have to know the load cycle of the transformer i.e. how
much and how long the transformer is loaded during 24 hours.

9. Example 14.13 Determine the all-day efficiency of a 10 kVA 2220/220V 60 Hz
transformer. During a day of 24 hours, it is loaded with unity power factor as under
the following condition: 2 hours at five-fourths load; 6 hours at full load; 8 hours at
half load; 4 hours at one-quarter load; 4 hours at no load. Take core loss as 153 W
and full-load copper loss as 224 W.
Solution:

10. The energy loss due to core loss is= 24153 = 3672 W-hr=3.672 kW-hr
Total energy loss= 3.672 + 2.548 = 6.22 kW-hr
Total energy input= 135.0 + 6.22 = 141.22 kW-hr
%6.95or956.0
22.141
135
ontput
output
dayall



Example 32.55: Find the all-day efficiency of 500kVA distribution transformer
where copper loss at full load is 4.5kW and iron loss is 3.5kW. During a day of 24
hours, it is loaded as under
Solution: It should be noted that a load of 400 kW at 0.8 pf is equal to
800/0.8=500kVA.
Similarly, 300 kW at 0.75 pf means 300/0.75=400 kVA
and 100 kW at 0.8 pf means 100/0.8=125 kVA i.e. one fourth of the full load.
Cu loss at F.L. of 500 kVA= 4.5 kW
Cu loss at 400 kVA= 4.5(400/500)2=2.88 kW

11. Cu loss at 125 kVA= 4.5(125/500)2=0.281 kW
The total Cu loss in 24 hours =(64.5)+(102.88)+(40.281)+(40)=27+28.8+1.124=56.924
kWh
The iron loss takes place throughout the day irrespective of the load on the transformer
because its primary is energized all the 24 hours.
So, iron loss in 24 hours = 243.5= 84 kWh
Total transformer loss=56.924+84=140.924 kWh
Transformer output in 24 hours= (6400)+(10300)+(4100)= 5800 kWh
%6.97or976.0
924.1405800
5800
lossesoutput
output
dayall
So, 







12. Three Phase Transformer
Large-scale generation of electric power is usually 3-phase at generated voltage of
11 kV or 13.2 kV or somewhat higher.
Transmission is generally accomplished at higher voltage of 110, 132, 275, 400 and
750 kV for which purpose 3-phase transformers are necessary to step up the
generated voltage to that of the transmission line.
At load centers, the transmission voltages are reduced to distribution voltages of
6.6, 4.6 and 2.3 kV.
At most of the consumers, the distribution voltages are still reduced to utilization
voltages of 440, 220 or 110 volts.
Years ago, it was a common practice to use suitably interconnected three single-
phase transformers instead of a single three-phase transformer.
But these days, the latter is gaining popularity because of improvement in design
and manufacture.
As compared to a bank of single-phase transformers, the main advantages of a 3-
phase transformer are that it occupies less floor space for equal rating, weighs less,
cost about 15% less and further, that only one unit is to be handled and connected.
Like single-phase transformers, the three phase transformers are also of the core
type and shell type.

13. Three-Phase Transformer Connections
Three-phase power may be transformed by using combinations of single-phase
transformers.
The primaries may be connected in either Y (Wye) or  (Delta), and with either
type of primary connection, secondaries may likewise be connected either way.
Thus, the most common connection are (i) star/star or Y-Y, (ii) -, (iii) Y-, (iv) -
Y, (v) open delta or V-V, and (vi) Scott connection or T-T connection.
Star/Star or Y-Y
This connection is most economical for small, high-voltage transformers because the
number of turns/phase and the amount of insulation required are minimum (as phase
voltage is only 1/3 of line voltage).
The ratio of line voltages on the primary and secondary sides is the same as the
transformation ratio of each transformer.
However, there is a phase shift of 30o between the phase voltages and line voltages both
on the primary and secondary sides.
This connection works satisfactorily only if the load is balanced.

14. In Fig. 33.4 is shown a bank of 3 transformers connected in Y on both the primary
and the secondary sides.
With the unbalanced load to the neutral, the neutral point
shifts thereby making the three line-to-neutral (i.e. phase)
voltages unequal.
This difficulty of shifting neutral can be obviated by
connecting the primary neutral (shown dotted in the
figure) back to the generator so that primary coil A can
take its required power from between its line and the
neutral.
Another advantage of stabilizing the primary neutral by
connecting it to neutral of the generator is that it
eliminates distortion in the secondary phase voltages.
For delivering a sine wave of voltage, it is necessary to
have a sine wave of flux in the core, but on account of the
characteristic of iron, a sine wave of flux requires a third
harmonic component in the exciting current.
If the primary neutral isolated, the triple frequency
current cannot flow.Hence, the flux in the core cannot be a sine wave and so the voltages are distorted.
But if the primary neutral earthed i.e. joined to the generator neutral, then this
provides a path for the triple-frequency currents and emfs and the difficulty is
overcome.

15. Delta-Delta or - Connection
This connection is economical for large, low-voltage transformers in which insulation
problem is not so urgent, because its increases the number of turns/phase.
The transformer connections and voltage triangles are shown in Fig. 33.5.
The ratio of transformation between primary and secondary line voltage is exactly
the same as that of each transformer.
Further, the secondary voltage triangle abc occupies the same relative position as
the primary voltage triangle ABC i.e. there is no angular displacement between the
two.
This connection has the following advantages:
1. The third harmonic component of the magnetizing current
can flow in the -connected transformer primaries without
flowing in the line wires. Therefore the flux is sinusoidal which
results in sinusoidal voltages.
2. No difficulty is experienced from the unbalanced loading as
was the case in Y-Y connection. The three-phase voltages
remain practically constant regardless of load imbalance.
3. If one transformer becomes disabled, the system can
continue to operate in open-delta or in V-V although with
reduced available capacity.

16. Wye-Delta or Y- Connection
The main use of this connection is at the substation end of the transmission line where the
voltage is to be stepped down.
The primary windings is Y-connected with grounded neutral as shown in Fig. 33.6.
The ratio between the secondary and primary line voltage is
1/3 times the transformation ratio of each transformer.
There is a 30o shift between the primary and secondary line
voltages which means that a Y- transformer bank cannot be
paralleled with either a Y-Y or a - bank.
Also, third harmonic currents flows in the  to provide a
sinusoidal flux.

17. Delta-Wye or -Y Connection
This connection is generally employed where it is necessary to
step up the voltage as for example, at the beginning of high
tension transmission system.
The connection is shown in Fig. 31.7.
In this connection, the primary and secondary line voltages
and line currents are out of phase with each other by 30o.
Because of this 30o shift, it is impossible to parallel such a
bank with a - or Y-Y bank of transformers even though the
voltage ratios are correctly adjusted.
The ratio of secondary to primary voltage is 3 time the
transformation ratio of each transformer.

18. Open-Delta or V-V Connection
If one of the transformers of a - is removed and 3-phase supply is connected to the
primaries as shown in Fig. 33.11, then three equal 3-phase voltages will be available at the
secondary terminals on no-load.
It is employed:
1. when the three phase load is too small to warrant the
installation of full three-phase transformer bank.
2. when one of the transformers in a - bank is disabled, so
that service is continued although at reduced capacity, till the
faculty transformer is repaired or a new one is sustained.
3. when it is anticipated that in future the load will increase
necessitating the closing of open delta.

19. As seen from Fig. 33.12(a)
- capacity = 3VL.IL=3VL.( 3IS)=3VLIS
In Fig. 33.12(b), it is obvious that when - bank becomes V-V bank, the secondary line
current IL becomes equal to the secondary phase current IS.
V-V capacity = 3VL.IL=3VL.IS (Since line current and phase current are equal)
%58or577.0
3
1
3
3
capacity-
capacityThus, 
S
I
L
V
S
I
L
V

VV
It means that the capacity of V-V transformer is 57.7% (or 1/3 times) of the capacity of -
 transformer.

20. The disadvantages of V-V connection are:
1. The average power factor at which the V-bank
operates is less than that of the load. This power factor
is actually 86.6 of the balanced load power factor.
2. Secondary terminal voltages tend to become
unbalanced to a great extent when the load is
increased, this happens even when the load is perfectly
balanced.