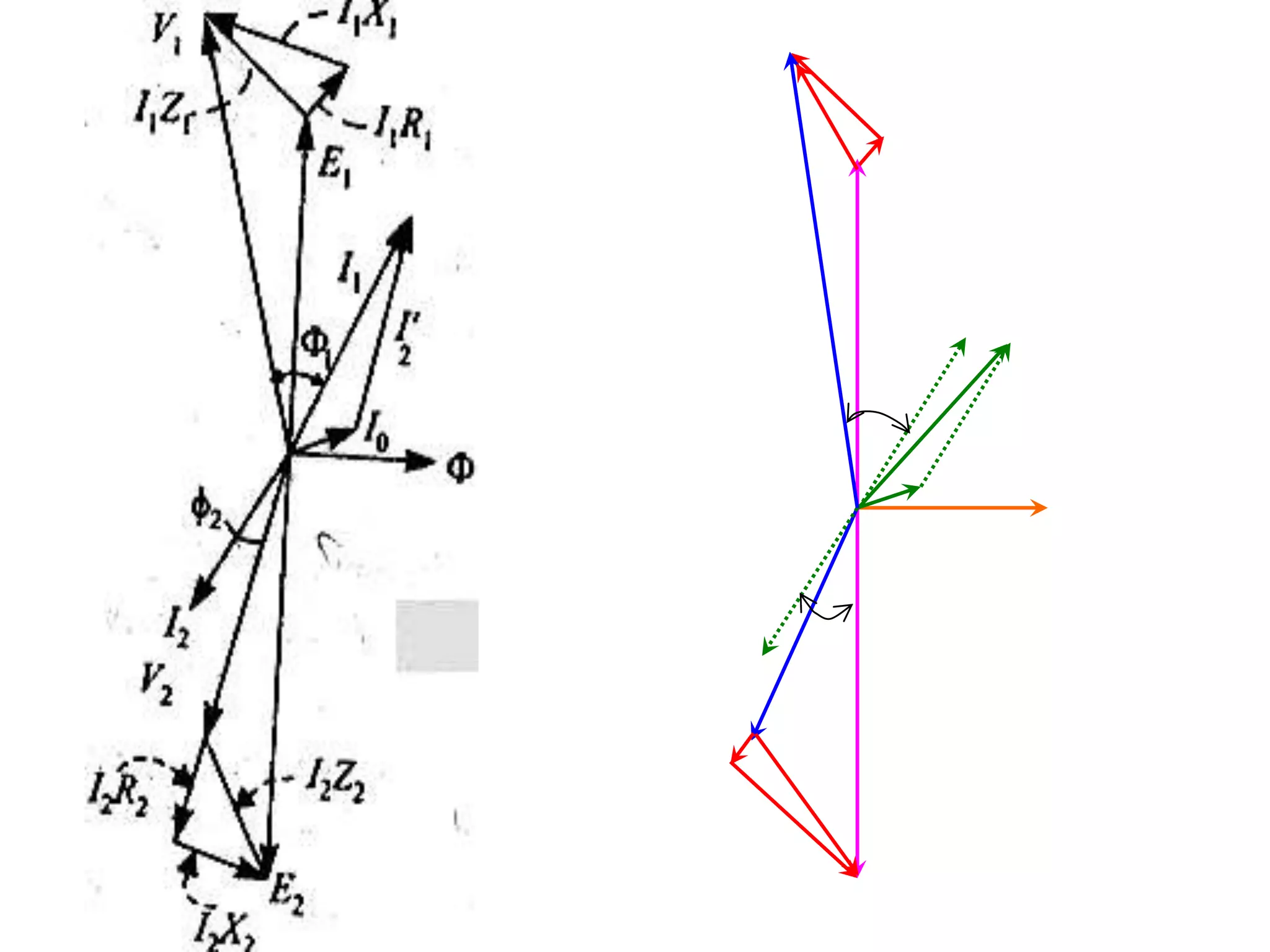
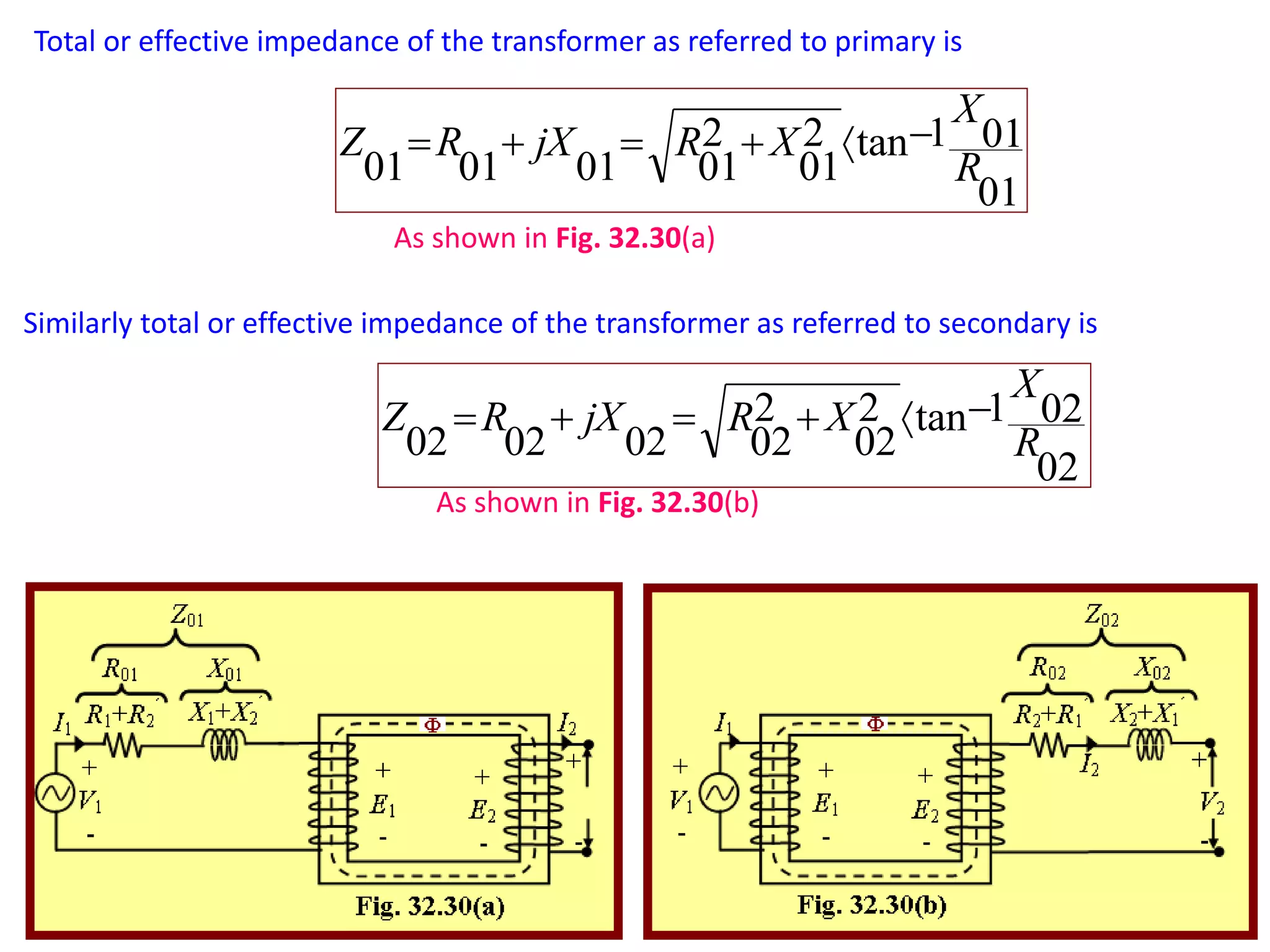
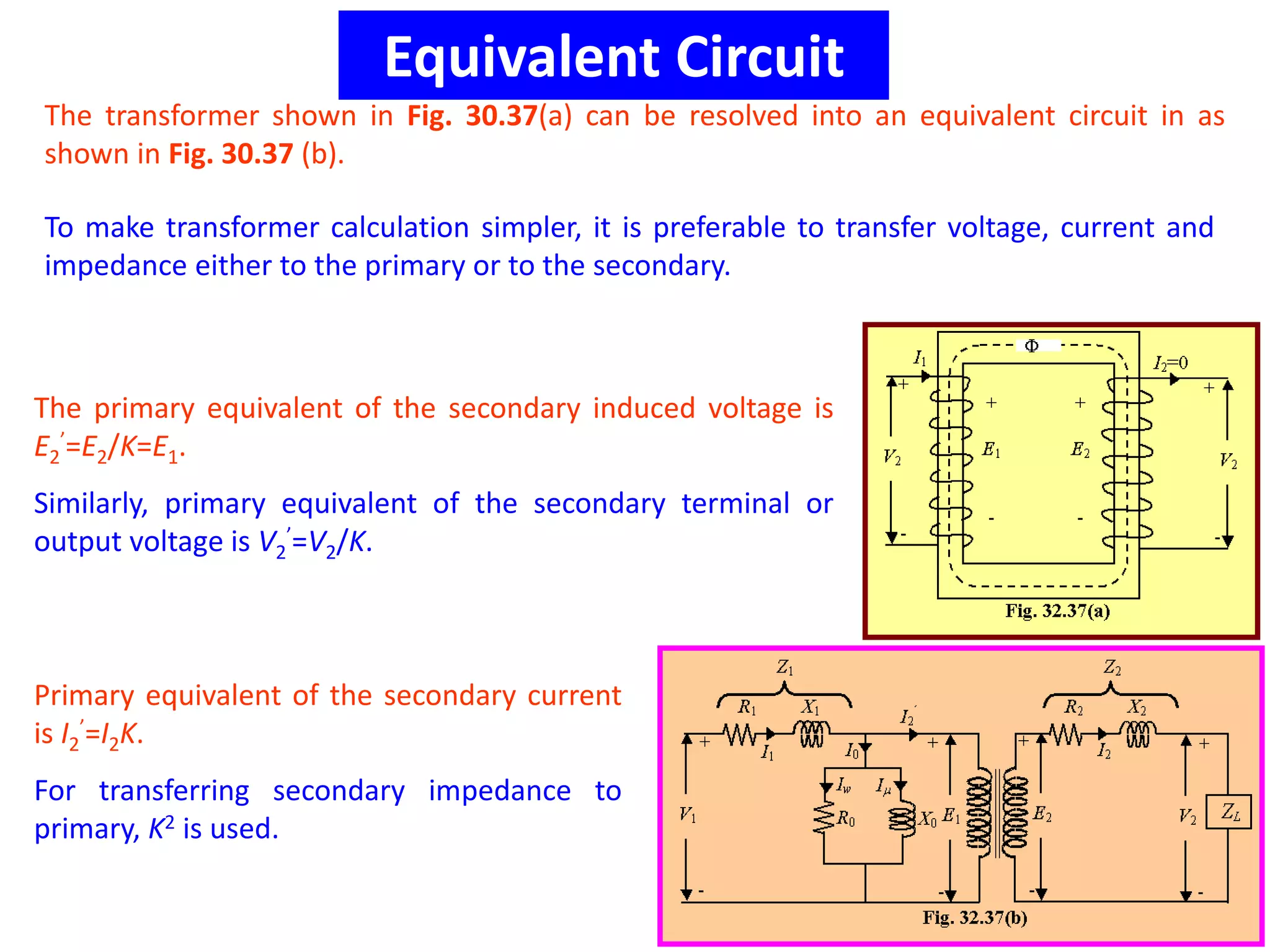
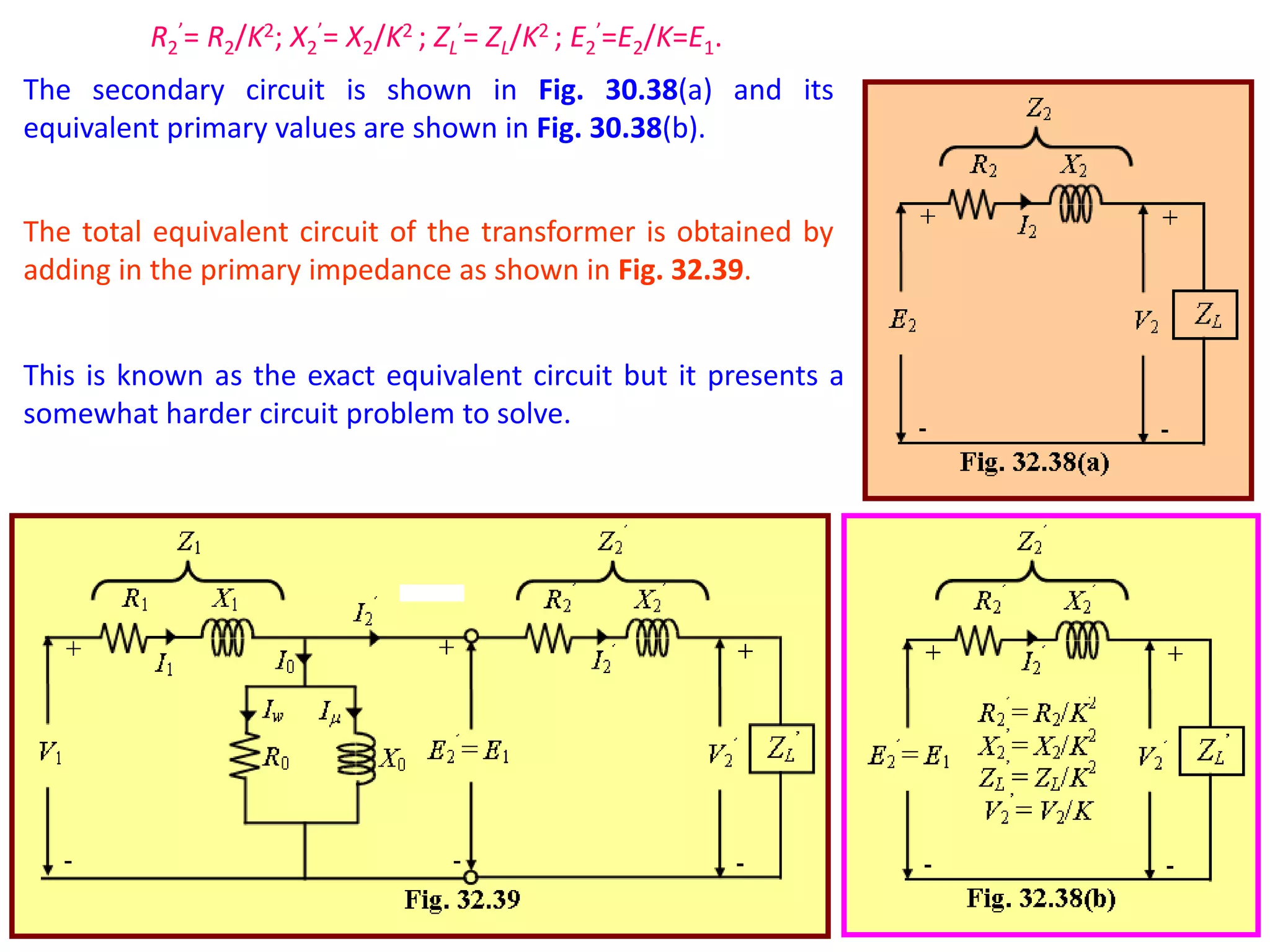
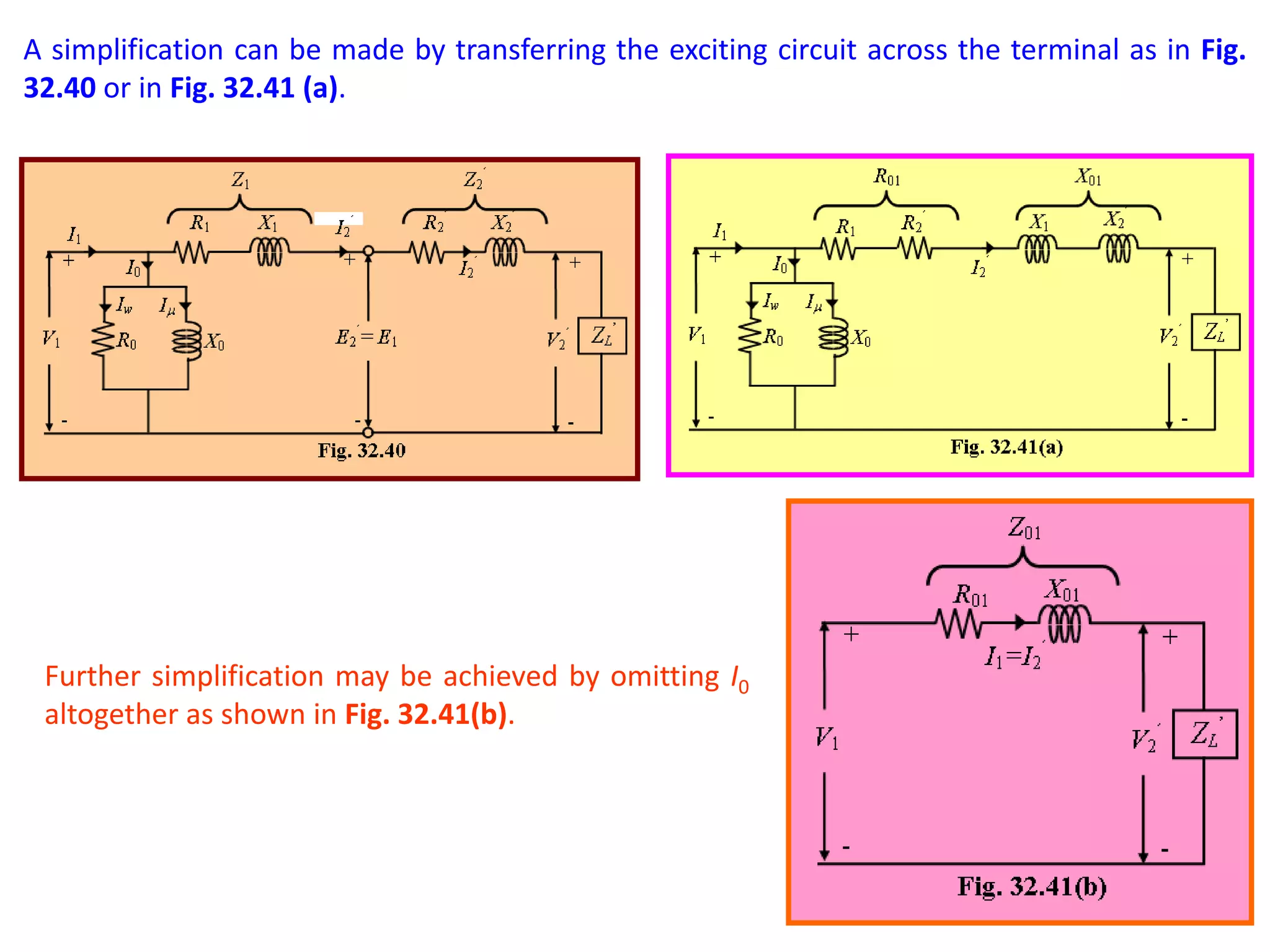
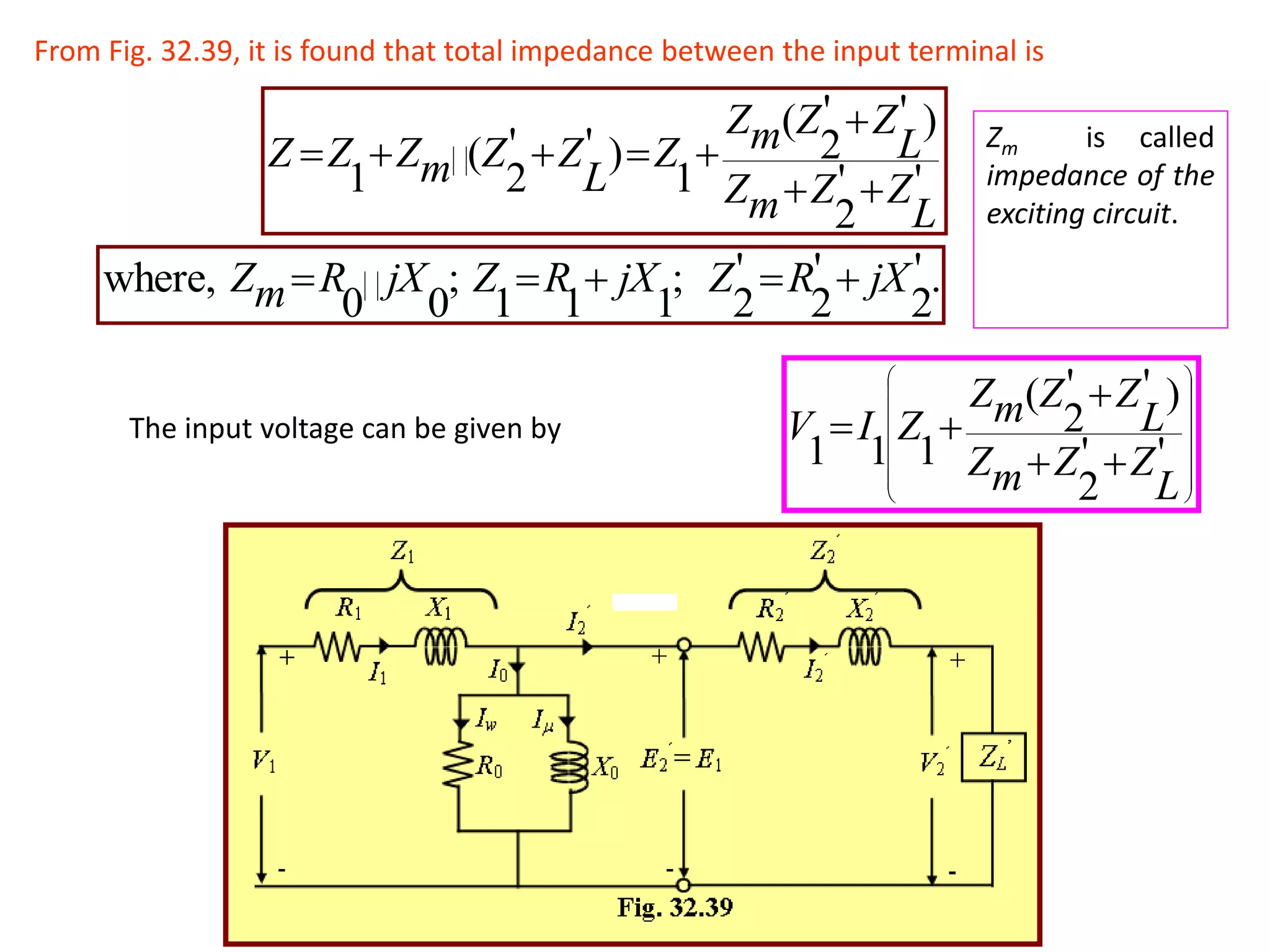
1) The equivalent resistance, reactance, and impedance of the transformer windings can be transferred from one winding to the other to simplify calculations. This is done by dividing the secondary values by the transformer ratio (K). 2) The equivalent circuit model represents the transformer using resistances and reactances for both the primary and secondary windings referred to a single winding for simplicity. Additional impedances are included for the magnetizing current. 3) Simplified equivalent circuits omit some components like the magnetizing current to make the circuit problems easier to solve while still capturing the essential transformer behavior.

1. Lecture 6

2. Inductive Load
• In the case of inductive load, the secondary
voltage I2 leads V2 by an angle 2.
• The angle 1 between V1 and I1 gives the
power factor angle of the transformer.

4. Equivalent Resistance, Reactance and Impedance
The resistances and reactance of the two windings of a transformer can be
transferred to any one of the tow windings.
The advantage of concentrating both resistances and reactances in one winding is
that it makes calculations very simple and easy because one has then to work in
one winding only.
It will be provided that the resistance R2, X2, in secondary is equivalent to R2/K2,
X2/K2 in primary.
The value R2/K2, X2/K2 will be denoted by R2
’, X2
’ the equivalent secondary
resistance as referred to primary.
The power loss of resistance R2 in secondary is= I2
2R2.
The power loss of resistance R2
’ when R2 is referred to in secondary is= I1
2R2’.
Equating the above two power, we obtain
2
2
2
'
2
2
1
RIRI 
2
2
2
2
1
2'
2
or
K
R
R
I
I
R 










Similarly, equivalent primary resistance as referred to secondary is
2
1
'
1
KRR 

5. Similarly, the leakage reactances can also be transferred from one winding to the other in the
same way as resistance. Thus
2
1
'
1
and2/
2
'
2
KXXKXX 
Total or effective resistance and reactance of the transformer as referred to primary is
2/
21
'
2101
Similarly,
2/
21
'
2101
primarytoreferredasresistancesecondaryequivalentresistanceprimary
01
KXXXXX
KRRRRR
R



Similarly total or effective resistance of the transformer as referred to secondary is
2
12
'
1202
Similarly,
2
12
'
1202
primarytoreferredasresistanceprimaryequivalentresistancesecondary
02
KXXXXX
KRRRRR
R




6. Total or effective impedance of the transformer as referred to primary is
Similarly total or effective impedance of the transformer as referred to secondary is
01
011tan2
01
2
01010101 R
X
XRjXRZ 
02
021tan2
02
2
02020202 R
X
XRjXRZ 
As shown in Fig. 32.30(a)
As shown in Fig. 32.30(b)

7. Equivalent Circuit
The transformer shown in Fig. 30.37(a) can be resolved into an equivalent circuit in as
shown in Fig. 30.37 (b).
To make transformer calculation simpler, it is preferable to transfer voltage, current and
impedance either to the primary or to the secondary.
The primary equivalent of the secondary induced voltage is
E2
’=E2/K=E1.
Similarly, primary equivalent of the secondary terminal or
output voltage is V2
’=V2/K.
Primary equivalent of the secondary current
is I2
’=I2K.
For transferring secondary impedance to
primary, K2 is used.

8. The secondary circuit is shown in Fig. 30.38(a) and its
equivalent primary values are shown in Fig. 30.38(b).
R2
’= R2/K2; X2
’= X2/K2 ; ZL
’= ZL/K2 ; E2
’=E2/K=E1.
The total equivalent circuit of the transformer is obtained by
adding in the primary impedance as shown in Fig. 32.39.
This is known as the exact equivalent circuit but it presents a
somewhat harder circuit problem to solve.

9. A simplification can be made by transferring the exciting circuit across the terminal as in Fig.
32.40 or in Fig. 32.41 (a).
Further simplification may be achieved by omitting I0
altogether as shown in Fig. 32.41(b).

10. From Fig. 32.39, it is found that total impedance between the input terminal is
''
2
)''
2
(
1
)''
2
(
1
L
ZZmZ
L
ZZmZ
Z
L
ZZmZZZ



.'
2
'
2
'
2
;
111
;
00
where, jXRZjXRZjXRmZ 
Zm is called
impedance of the
exciting circuit.

















''
2
)''
2
(
111
L
ZZmZ
L
ZZmZ
ZIVThe input voltage can be given by