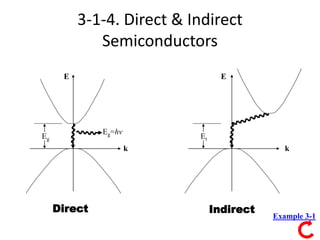
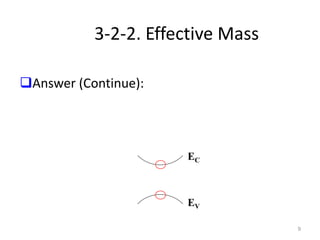
1) The document discusses direct and indirect semiconductors, explaining that direct semiconductors have a minimum energy (Eg) that occurs at the same crystal momentum (k) while indirect semiconductors have a minimum energy (Eg) that occurs at different k values. 2) It also covers effective mass, which is used instead of free electron mass when applying equations of electrodynamics to charge carriers in solids. Effective mass depends on the curvature of the energy-momentum relationship. 3) The document describes how electrons and holes behave as quantum particles when confined in a thin semiconductor layer between barriers of a different semiconductor, resulting in discrete energy levels instead of a continuum.

1. 1
3-1-4. Direct & Indirect
Semiconductors
• A single electron is assumed to travel through a
perfectly periodic lattice.
• The wave function of the electron is assumed to
be in the form of a plane wave moving.
xjk
xk
x
exkUx ),()( 
 x : Direction of propagation
 k : Propagation constant / Wave vector
  : The space-dependent wave function for the electron

2. 2
3-1-4. Direct & Indirect
Semiconductors
 U(kx,x): The function that modulates the wave function according to the
periodically of the lattice.
 Since the periodicity of most lattice is different in various directions, the (E,k)
diagram must be plotted for the various crystal directions, and the full
relationship between E and k is a complex surface which should be visualized
in there dimensions.

3. 3
3-1-4. Direct & Indirect
Semiconductors
Eg=hν
Eg Et
k k
EE
Direct Indirect
Example 3-1

4. 4
3-1-4. Direct & Indirect
Semiconductors
Example 3-1:
Assuming that U is constant in
for an essentially free electron, show that the
x-component of the electron momentum in the
crystal is given by
xx khP 
Example 3-2
),()( xkUx xk 
xjkx
e

5. 5
3-1-4. Direct & Indirect
Semiconductors
x
x
xjkxjk
x
kh
dxU
dxUkh
dxU
dxe
xj
h
eU
P
xx

















2
2
2
2
)(Answer:
The result implies that (E,k) diagrams such as shown in previous figure can be considered
plots of electron energy vs. momentum, with a scaling factor .
h

6. 6
3-2-2. Effective Mass
• The electrons in a crystal are not free, but
instead interact with the periodic
potential of the lattice.
• In applying the usual equations of
electrodynamics to charge carriers in a
solid, we must use altered values of
particle mass. We named it Effective
Mass.

7. 7
3-2-2. Effective Mass
Example 3-2:
Find the (E,k) relationship for a free electron
and relate it to the electron mass.
E
k

8. 8
3-2-2. Effective Mass
khmvp 
2
22
2
22
1
2
1
k
m
h
m
p
mvE 
Answer:
From Example 3-1, the electron momentum is:
m
h
dk
Ed 2
2
2


9. 9
3-2-2. Effective Mass
Answer (Continue):
Most energy bands are close to parabolic at their
minima (for conduction bands) or maxima (for
valence bands).
EC
EV

10. 10
3-2-2. Effective Mass
• The effective mass of an electron in a band
with a given (E,k) relationship is given by
2
2
2
*
dk
Ed
h
m 

X
L
k
E
1.43eV
)()( or
**
LXmm 
Remember that in GaAs:

11. 11
3-2-2. Effective Mass
• At k=0, the (E,k) relationship near the minimum
is usually parabolic:
gEk
m
h
E  2
*
2
2
In a parabolic band, is constant. So, effective mass is constant.
Effective mass is a tensor quantity.
2
2
dk
Ed
2
2
2
*
dk
Ed
h
m 

12. 12
3-2-2. Effective Mass
EV
EC
02
2

dk
Ed
02
2

dk
Ed
0*
m
0*
m
2
2
2
*
dk
Ed
h
m 
Ge Si GaAs
† m0 is the free electron rest mass.
Table 3-1. Effective mass values for Ge, Si and GaAs.
mn
*
mp
*
055.0 m 01.1 m 0067.0 m
037.0 m 056.0 m 048.0 m

13. 13
3-2-5. Electrons and Holes in Quantum
Wells
• One of most useful applications of MBE or
OMVPE growth of multilayer compou-nd
semiconductors is the fact that a
continuous single crystal can be grown in
which adjacent layer have different band
gaps.
• A consequence of confining electrons and
holes in a very thin layer is that

14. 14
3-2-5. Electrons and Holes in Quantum
Wells
these particles behave according to the
particle in a potential well problem.
GaAs Al0.3Ga0.7AsAl0.3Ga0.7As
50Å
E1
Eh
1.43eV1.85eV
0.28eV
0.14eV
1.43eV

15. 15
3-2-5. Electrons and Holes in
Quantum Wells
• Instead of having the continuum of states as
described by ,modified for
effective mass and finite barrier height.
• Similarly, the states in the valence band
available for holes are restricted to discrete
levels in the quantum well.
2
222
2mL
hn
En



16. 16
3-2-5. Electrons and Holes in
Quantum Wells
• An electron on one of the discrete condu-ction
band states (E1) can make a transition to an
empty discrete valance band state in the GaAs
quantum well (such as Eh), giving off a photon
of energy Eg+E1+Eh, greater than the GaAs band
gap.