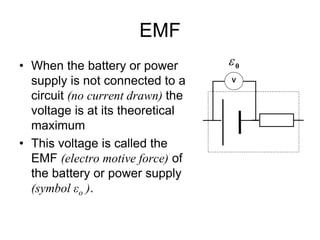
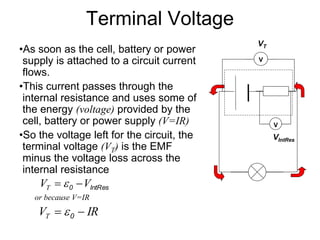
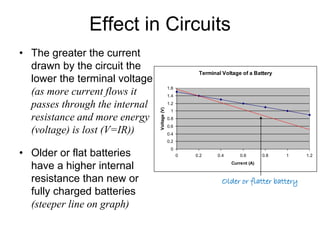
This document discusses the internal resistance of batteries and power supplies. It explains that batteries and power supplies behave as if they have a series resistor inside them, called the internal resistance. When a battery is connected to a circuit, current flows through the internal resistance, causing a voltage drop and reducing the terminal voltage from the theoretical EMF voltage. The greater the current drawn from the battery, the greater the voltage drop due to the internal resistance.