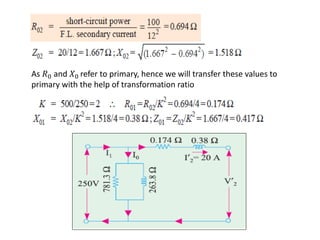
The document discusses transformer ratings, efficiency, and power factor. It explains that transformers are rated in kVA rather than kW because manufacturers do not know the load power factor in advance. Maximum efficiency occurs when iron losses equal copper losses. Transformer efficiency is calculated based on output power in watts rather than volt-amperes. Low power factor reduces efficiency by decreasing the output power relative to losses. Correcting power factor can help increase efficiency when a transformer is overloaded.

1. Transformer Efficiency
Transformer Rating
Transformer Regulation
Condition for maximum Efficiency

2. Why Transformers are Rated in kVA, Not in kW?
Rating of a transformer or any electrical machine reflects its load carrying
capability without overheating. Core Losses of the transformer depends on
Voltage (V) and Copper losses ( I²R) depends on Current (A) which passes
through the transformer. That's why the rating of Transformer in kVA, not in
kW.
When a manufacturer makes a transformer, they have no idea of the type of
load that will be used & consequently they can only rate the device according
to its maximum current output that the conductors can safely carry (at unity
Power Factor) & the insulation rating of the conductors (voltage &
temperature). So the transformer is designed for rated voltage and rated
current. We can't predict the power factor while designing the machine,
because power factor depends upon the load which varies time to time.
That’s why the Transformer Rating is expressed in kVA, not in kW.

3. Regulation of a Transformer
The measure of how well a power transformer maintains constant
secondary voltage over a range of load currents is called the transformer’s
voltage regulation. It can be calculated from the following formula:

4. As the transformer is loaded, the secondary terminal voltage falls (for a
lagging p.f.). Hence, to keep the output voltage constant, the primary
voltage must be increased. Suppose primary voltage has to be raised from
its rated value 𝑉1 to 𝑉1 ’, then

5. Problem: A 250/500-V transformer gave the following test results :
OC test : 250 V, 1 A, 80 W on low-voltage side.
SC test : with low-voltage winding short-circuited :20 V; 12 A, 100 W .
Determine the equivalent circuit parameters and insert them on the equivalent circuit
diagram and calculate the full load efficiency when the output is 10 A at 500 volt and
0.8 power factor lagging.
Solution. Open-circuit Test :

6. As 𝑅0 and 𝑋0 refer to primary, hence we will transfer these values to
primary with the help of transformation ratio

8. Efficiency of a Transformer
Efficiency =
Output
Input
A better method is to determine the losses and then to calculate the
efficiency from ;
or
It may be noted here that efficiency is based on power output in watts and
not in volt-amperes, al- though losses are proportional to VA. Hence, at any
volt-ampere load, the efficiency depends on power factor, being maximum at
a power factor of unity.

9. Condition for Maximum Efficiency
Considering primary side,
or, η
….. (1)
Differentiating both sides of equation (1) with respect to 𝐼1, we get

10. Condition for Maximum Efficiency
….. (2)
For η to be maximum, Hence, the equation (2) becomes
or Iron loss = Cu loss

11. All- day Efficiency
The ordinary or commercial efficiency of a transformer is given by the ratio
But there are certain types of transformers whose performance cannot be
judged by this efficiency; distribution transformers have their primaries
energized all the twenty-four hours, although their secondaries supply little or
no-load much of the time during the day except during the house lighting
period. The performance of such is compared on the basis of energy consumed
during a certain time period, usually a day of 24 hours

12. Problem: A 10 kVA, 500/250 V, single-phase transformer gave the following test results:
S.C. Test (H.V. side) : 60 V, 20 A, 150 W
The maximum efficiency occurs at unity power factor and at 1.20 times full-load current.
Determine full-load efficiency at 0.80 p.f. Also calculate the maximum efficiency.
Solution. Full-load current on H.V. side = 10,000/500 = 20 Amp
S.C. test has been conducted from H.V. side only. Hence, at unity p.f. , full-load
copper-loss is = 150 watts
(a) Maximum efficiency occurs at 1.2 times of full-load current,
So, at unity p.f. corresponding copper loss is = (1.2)2
x 150 = 216 watts
At maximum efficiency, copper-loss = core-loss = 216 watts
Corresponding Power-output = 1.2 x 10,000 x 1.0 = 12 kW
Hence, maximum efficiency at unity P.f. = (12)/(12 + 0.216 + 0.2160) = 0.9653 = 96.53 %

13. Problem: A 10 kVA, 500/250 V, single-phase transformer gave the following test results:
S.C. Test (H.V. side) : 60 V, 20 A, 150 W
The maximum efficiency occurs at unity power factor and at 1.20 times full-load current.
Determine full-load efficiency at 0.80 p.f. Also calculate the maximum efficiency.
Solution
(b) Full-load efficiency at 0.80 P.f.
Output Power at full-load, 0.80 P.f. = 10,000 x 0.8 = 8000 W, constant core-loss = 216 W
Corresponding copper-loss = 150 W
Total losses = 366 W
Hence, efficiency = (8000/8366) x 100 % = 95.63 %.

14. Conclusion

15. Say our substation is loaded to the maximum transformer capacity and we know it is
delivering power at a poor power factor. Our options are:
1. unload the transformer by disconnecting loads from it,
2. buy a larger transformer,
3. provide additional cooling to it (this raises the transformer capacity) or
4. correct the power factor.
Power Factor (P.F.) is the ratio of Working Power to Apparent Power.
P.F. =
𝐾𝑊
𝐾𝑉𝐴

16. Lagging and Leading Power Factors:
In addition, there is also a difference between a lagging and leading power factor. A lagging
power factor signifies that the load is inductive, as the load will “consume” reactive power,
and therefore the reactive component Q is positive as reactive power travels through the
circuit and is “consumed” by the inductive load. A leading power factor signifies that the
load is capacitive, as the load “supplies” reactive power, and therefore the reactive
component Q is negative as reactive power is being supplied to the circuit.
If θ is the phase angle between the current and voltage, then the power factor is
equal to the cosine of the angle, :