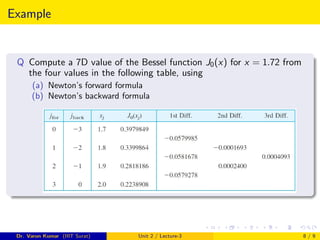
This document discusses Newton's forward and backward difference interpolation formulas for equally spaced data points. It provides the formulations for calculating the forward and backward differences up to the kth order. For equally spaced points, the forward difference formula approximates a function f(x) using its kth forward difference at the initial point x0. Similarly, the backward difference formula approximates f(x) using its kth backward difference at x0. The document includes an example problem of using these formulas to estimate the Bessel function and exercises involving interpolation of the gamma function and exponential function.

1. Equal Spacing: Newton’s Forward and Backward
Difference Interpolation
Dr. Varun Kumar
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-3 1 / 9

2. Outlines
1 Equal Spacing: Newton’s Forward Difference Formulation
Example
2 Equal Spacing: Newton’s Backward Difference Formulation
Example
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-3 2 / 9

3. Equal Spacing: Newton’s Forward Difference Formula
Important points
⇒ As per the Newton’s divide difference interpolation formula
f (x)= f0 + (x − x0)f [x0, x1] + (x − x0)(x − x1)f [x0, x1, x2] + ...+
(x − x0)(x − x1)....(x − xn−1)f [x0, ..., xn]
(1)
or
f [x0, ...., xk] =
f [x1, ....., xk] − f [x0, ...., xk−1]
xk − x0
⇒ Above expression is valid for arbitrarily spaced nodes.
⇒ In most of the practical experimentation, it can be adopted.
⇒ For some instances, the interval may be equi-spaced, i.e,
x0, x1 = x0 + h, x2 = x0 + 2h, ....., xn = x0 + nh (2)
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-3 3 / 9

4. Continued–
⇒ First forward difference of f at xj by
4fj = fj+1 − fj
⇒ Second forward difference of f at xj by
42
fj = 4fj+1 − 4fj
⇒ The kth forward difference of f at xj by
4k
fj = 4k−1
fj+1 − 4k−1
fj ∀ k = 1, 2, ...
⇒ In case of regular spacing in input (x), then
f [x0, x1, ....., xk] =
1
k!hk
4k
f0 (3)
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-3 4 / 9

5. Continued–
⇒ For k = 1, from (3)
f [x0, x1] =
f1 − f0
x1 − x0
=
1
h
(f1 − f0) =
1
1!h
4f0 (4)
⇒ Let xk+1 = x0 + (k + 1)h
f [x0, ......, xk+1] =
f [x1, ..., xk+1] − f [x0, ..., xk]
xk+1 − x0
=
1
(k + 1)h
h 1
k!hk
4k
f1 −
1
k!hk
4k
f0
i
=
1
(k + 1)!hk+1
4k+1
f0
(5)
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-3 5 / 9

6. Continued–
⇒ Applying Newton’s forward difference interpolation formula
f (x) ≈ pn(x) = f0 + r4f0 +
r(r − 1)
2!
42
f0 + ...+
r(r − 1)...(r − n + 1)
n!
4n
f0
(6)
where r = x−x0
h
Q Compute cosh 0.56. Utilize the four values in the following table and
estimate the error.
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-3 6 / 9

7. Equal Spacing: Newton’s Backward Difference Formulation
⇒ First backward difference of f at xj by
∇fj = fj − fj−1
⇒ Second backward difference of f at xj by
∇2
fj = ∇fj − ∇fj−1
⇒ kth backward difference of f at xj by
∇k
fj = ∇k−1
fj − ∇k−1
fj−1 (7)
⇒ As per Newton’s backward difference interpolation formula
f (x) ≈ pn(x) = f0 + r∇f0 +
r(r + 1)
2!
∇2
f0 + ... +
r(r + 1)...(r + n − 1)
n!
∇n
f0
(8)
where r = x−x0
h
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-3 7 / 9

8. Example
Q Compute a 7D value of the Bessel function J0(x) for x = 1.72 from
the four values in the following table, using
(a) Newton’s forward formula
(b) Newton’s backward formula
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-3 8 / 9

9. Exercise Problem
1 Calculate the Lagrange polynomial p2(x) for the values
Γ(1.00) = 1.0000, Γ(1.02) = 0.9888, Γ(1.04) = 0.9784 of the gamma
function and from it approximate Γ(1.01) and Γ(1.03).
2 Find e−0.25 and e−0.75 by linear interpolation of e−x with x0 = 0,
x1 = 0.5, and x0 = 0.5, x1 = 0, respectively. Then find p2(x) by
quadratic interpolation of e−x with x0 = 0, x1 = 0.5, and x2 = 1 and
from it e−0.25 and e−0.75 compare the errors.
3 Solve the above problem using Newton’s divide and difference
interpolation method.
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-3 9 / 9