Recommended
Recommended
More Related Content
What's hot
What's hot (20)
Similar to Newton's Backward Interpolation Formula with Example
Similar to Newton's Backward Interpolation Formula with Example (20)
Recently uploaded
Recently uploaded (20)
Newton's Backward Interpolation Formula with Example
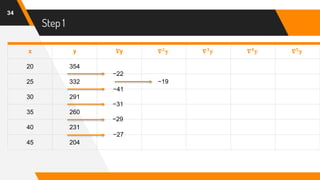
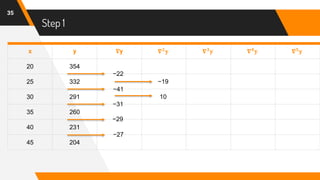
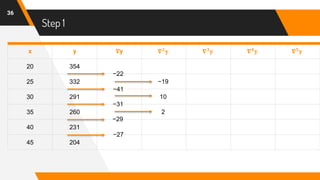
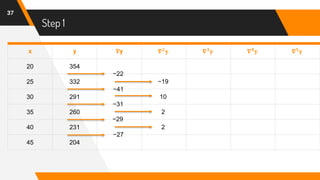
- 1. Numerical Analysis Newton’s Backward Interpolation Formula Presented By: Muhammad Usman Ikram (F2018266065)
- 2. What is Interpolation ? 2
- 3. “Interpolation is a type of estimation, a method of constructing new data points within the range of a discrete set of known data points.
- 4. Example Year (x) 1990 1995 2000 2005 2010 Sales (y) (in millions) 57 63 64 68 70 4
- 5. History 5
- 6. History ▸ 300 BC Babylonian astronomers used linear and higher-order interpolation to fill gaps in ephemerides of the sun, moon, and the then- known planets. 6
- 7. History ▸ 1000 A.D The Arabian scientist Al-Biruni writes his major work Al-Qanun'l-Mas'udi , in which he describes a method for second-order interpolation. 7
- 8. Types of Interpolation (For equally-spaced data) ▸ Newton Forward Interpolation ▸ Newton Backward Interpolation ▸ Stirling’s Interpolation ▸ Gauss’s Forward Interpolation Formula ▸ Gauss’s Backward Interpolation Formula 8
- 10. The Backward Difference Table 10 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲
- 11. The Backward Difference Table 11 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 x0 x1 x2 x3 x4
- 12. The Backward Difference Table 12 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 x0 y0 x1 y1 x2 y2 x3 y3 x4 y4
- 13. The Backward Difference Table 13 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 x0 y0 x1 y1 x2 y2 x3 y3 x4 y4 𝛻y1 = y1 − y0
- 14. The Backward Difference Table 14 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 x0 y0 x1 y1 x2 y2 x3 y3 x4 y4 𝛻y1 = y1 − y0 𝛻y2 = y2 − y1
- 15. The Backward Difference Table 15 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 x0 y0 x1 y1 x2 y2 x3 y3 x4 y4 𝛻y1 = y1 − y0 𝛻y2 = y2 − y1 𝛻y3= y3 − y2
- 16. The Backward Difference Table 16 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 x0 y0 x1 y1 x2 y2 x3 y3 x4 y4 𝛻y1 = y1 − y0 𝛻y2 = y2 − y1 𝛻y3= y3 − y2 𝛻y4= y4 − y3
- 17. The Backward Difference Table 17 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 x0 y0 x1 y1 𝛻2 y2 x2 y2 x3 y3 x4 y4 𝛻y1 = y1 − y0 𝛻y2 = y2 − y1 𝛻y3= y3 − y2 𝛻y4= y4 − y3
- 18. The Backward Difference Table 18 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 x0 y0 x1 y1 𝛻2 y2 x2 y2 𝛻2 y3 x3 y3 x4 y4 𝛻y1 = y1 − y0 𝛻y2 = y2 − y1 𝛻y3= y3 − y2 𝛻y4= y4 − y3
- 19. The Backward Difference Table 19 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 x0 y0 x1 y1 𝛻2 y2 x2 y2 𝛻2 y3 x3 y3 𝛻2 y4 x4 y4 𝛻y1 = y1 − y0 𝛻y2 = y2 − y1 𝛻y3= y3 − y2 𝛻y4= y4 − y3
- 20. The Backward Difference Table 20 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 x0 y0 x1 y1 𝛻2 y2 x2 y2 𝛻2 y3 x3 y3 𝛻2 y4 x4 y4 𝛻y1 = y1 − y0 𝛻y2 = y2 − y1 𝛻y3= y3 − y2 𝛻y4= y4 − y3 𝛻3 y3
- 21. The Backward Difference Table 21 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 x0 y0 x1 y1 𝛻2 y2 x2 y2 𝛻2 y3 x3 y3 𝛻2 y4 x4 y4 𝛻y1 = y1 − y0 𝛻y2 = y2 − y1 𝛻y3= y3 − y2 𝛻y4= y4 − y3 𝛻3 y4 𝛻3 y3
- 22. The Backward Difference Table 22 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 x0 y0 x1 y1 𝛻2 y2 x2 y2 𝛻2 y3 𝛻4 y4 x3 y3 𝛻2 y4 x4 y4 𝛻y1 = y1 − y0 𝛻y2 = y2 − y1 𝛻y3= y3 − y2 𝛻y4= y4 − y3 𝛻3 y4 𝛻3 y3
- 23. The Backward Difference Table 23 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 x0 y0 x1 y1 𝛻2 y2 x2 y2 𝛻2 y3 𝛻4 y4 x3 y3 𝛻2 y4 x4 y4 𝛻y1 = y1 − y0 𝛻y2 = y2 − y1 𝛻y3= y3 − y2 𝛻y4= y4 − y3 𝛻3 y4 𝛻3 y3
- 24. Newton Backward Interpolation Formula 24 f(x) = 𝑦𝑛 + P𝛻𝑦𝑛 + P(P+1) 2! 𝛻2 𝑦𝑛 + P(P+1)(P+2) 3! 𝛻3 𝑦𝑛 + P(P+1)(P+2)(P+3) 4! 𝛻4 𝑦𝑛 + P(P+1)(P+2)(P+3)(P+4) 5! 𝛻5 𝑦𝑛 + _ _ _ _ _ _ _ _ _ _ _ Where xn = last value in column x yn = last value in column y ℎ = difference b/w values of x 𝑃 = 𝑥 − 𝑥 𝑛 ℎ
- 26. Question x 20 25 30 35 40 45 F(x) 354 332 291 260 231 204 26 ▸ Estimate f(42) for the following data
- 27. Step 1 27 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 25 30 35 40 45
- 28. Step 1 28 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 30 291 35 260 40 231 45 204
- 29. Step 1 29 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 30 291 35 260 40 231 45 204 −22
- 30. Step 1 30 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 30 291 35 260 40 231 45 204 −41 −22
- 31. Step 1 31 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 30 291 35 260 40 231 45 204 −31 −41 −22
- 32. Step 1 32 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 30 291 35 260 40 231 45 204 −29 −31 −41 −22
- 33. Step 1 33 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 30 291 35 260 40 231 45 204 −27 −29 −31 −41 −22
- 34. Step 1 34 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 −19 30 291 35 260 40 231 45 204 −27 −29 −31 −41 −22
- 35. Step 1 35 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 −19 30 291 10 35 260 40 231 45 204 −27 −29 −31 −41 −22
- 36. Step 1 36 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 −19 30 291 10 35 260 2 40 231 45 204 −27 −29 −31 −41 −22
- 37. Step 1 37 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 −19 30 291 10 35 260 2 40 231 2 45 204 −27 −29 −31 −41 −22
- 38. Step 1 38 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 −19 30 291 10 35 260 2 40 231 2 45 204 −27 −29 −31 −41 −22 29
- 39. Step 1 39 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 −19 30 291 10 35 260 2 40 231 2 45 204 −27 −29 −31 −41 −22 −8 29
- 40. Step 1 40 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 −19 30 291 10 35 260 2 40 231 2 45 204 −27 −29 −31 −41 −22 0 −8 29
- 41. Step 1 41 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 −19 30 291 10 −37 35 260 2 40 231 2 45 204 −27 −29 −31 −41 −22 0 −8 29
- 42. Step 1 42 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 −19 30 291 10 −37 35 260 2 8 40 231 2 45 204 −27 −29 −31 −41 −22 0 −8 29
- 43. Step 1 43 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 −19 30 291 10 −37 35 260 2 8 40 231 2 45 204 −27 −29 −31 −41 −22 0 −8 29 45
- 44. Step 1 44 x y 𝛁y 𝛁 𝟐 𝐲 𝛁 𝟑 𝐲 𝛁 𝟒 𝐲 𝛁 𝟓 𝐲 20 354 25 332 −19 30 291 10 −37 35 260 2 8 40 231 2 45 204 −27 −29 −31 −41 −22 0 −8 29 45
- 45. Step 2 45 x= 42 h= 5 xn = 45 yn = 204 𝑃 = 𝑥 − 𝑥 𝑛 ℎ 𝑃 = 42 −45 5 𝑃 = −3 5 𝑃 = - 0.6
- 46. Formula 46 f(x) = 𝑦𝑛 + P𝛻𝑦𝑛 + P(P+1) 2! 𝛻2 𝑦𝑛 + P(P+1)(P+2) 3! 𝛻3 𝑦𝑛 + P(P+1)(P+2)(P+3) 4! 𝛻4 𝑦𝑛 + P(P+1)(P+2)(P+3)(P+4) 5! 𝛻5 𝑦𝑛
- 47. Putting Values in Formula 47 f(42) = 204 + (-0.6)(-27) + (−0.6)[(−0.6)+1] 2 (2)+ (−0.6)[(−0.6)+1][(−0.6)+2] 6 (0) + (−0.6)[(−0.6)+1][(−0.6)+2][(−0.6)+3] 24 (8) + (−0.6)[(−0.6)+1][(−0.6)+2][(−0.6)+3][(−0.6)+4] 120 (45) = 204 + 16.2 + (−0.24) + 0 + (−0.26) + (−1.02) f(42) = 216.68
- 49. Advantages ▸ Helpful in estimation between given set of data. ▸ Simple and intuitive. ▸ Quick and easy. ▸ Helpful in images enhancing (image resizing) ▸ Helpful in Digital Signal Processing. 49
- 50. Disadvantages 50 ▸ Not always precise. ▸ Sometimes due to the fault in program used, image after resizing are blurry.
- 52. Applications in Computer Sciences ▸ Digital Image Processing Image interpolation works in two directions, and tries to achieve a best approximation of a pixel's intensity based on the values at surrounding pixels. 52 Original Image Enlarging Image to 183 % With InterpolationWithout Interpolation
- 53. Applications in Computer Sciences ▸ Game Development and Graphics Linear interpolation (commonly known as 'lerp') is a really handy function for creative coding, game development and generative art. It ensures the smooth movement of objects in games. 53
- 54. Sources Cited ▸ Interpolation - https://en.wikipedia.org/wiki/Interpolation ▸ A Chronology of Interpolation: From Ancient Astronomy to Modern Signal and Image Processing - http://bigwww.epfl.ch/publications/meijering0201.pdf ▸ Resizing Images - https://sisu.ut.ee/imageprocessing/book/3 ▸ Digital Image Interpolation - https://www.cambridgeincolour.com/tutorials/image- interpolation.htm ▸ A Brief Introduction to Lerp - https://www.gamedev.net/tutorials/programming/general-and-gameplay- programming/a-brief-introduction-to-lerp-r4954 ▸ Linear interpolation - https://en.wikipedia.org/wiki/Linear_interpolation 54
- 55. 55 JazakAllah