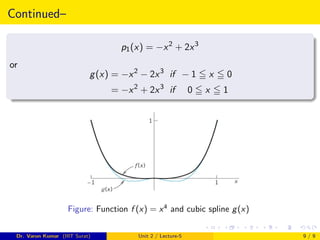
This document discusses cubic spline interpolation. Cubic splines are piecewise cubic polynomials that are continuously differentiable and match function values at sample points. They provide a smooth interpolation that avoids oscillations seen in higher-degree global polynomials. The document outlines the construction of cubic spline interpolation, including determining the coefficients for each cubic polynomial piece based on function values and derivatives at nodes. An example interpolates the function f(x)=x^4 on the interval [-1,1] using cubic splines.

1. Cubic Spline Interpolation
Dr. Varun Kumar
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-5 1 / 9

2. Outlines
1 Introduction to Splines
2 Cubic splines
3 Example
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-5 2 / 9

3. Introduction to Splines
Important points
⇒ Quality of interpolation increases with increasing degree n of the
polynomial used.
⇒ Above statement is not absolutely true for very large n.
⇒ For various function, the corresponding interpolation polynomials may
tend to oscillate more between the nodes causes numerical instability.
Figure: Runge’s example f (x) = 1
1+x2 and interpolation polynomial P10(x)
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-5 3 / 9

4. Continued–
⇒ Such oscillations are avoided by the method of splines.
⇒ Given f (x) on J, we partition J uniformly
a = x0 < x1.....xn = b (1)
⇒ We require the function g(x), which will interpolate f (x) on J.
⇒ Thus g(x0) = f (x0), ...., g(xn) = f (xn)
⇒ Obtained g(x) is called spline.
⇒ If f (x) is given on a 5 x 5 b and a partition (1) has been chosen, we
obtain a cubic spline g(x) that approximate f (x) by acquiring that
g(x0) = f (x0) = f0, g(x1) = f (x1) = f1, g(xn) = f (xn) = fn, (2)
g0
(x0) = k0 g0
(xn) = kn (3)
⇒ Note: k0 and kn are given number
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-5 4 / 9

5. Cubic splines
Theorem 1: Let f (x) be defined on the interval a 5 x 5 b, let a partition
(1) be given, and let k0 and kn be any two given numbers. Then there
exists one and only one cubic spline g(x) corresponding to (1) and
satisfying (2) and (3)
Important Results:
(1) cj−1kj−1 + 2(cj−1 + cj )kj + cj kj+1 = 3
h
c2
j−1∇fj + c2
j ∇fj+1
i
(2) Determination of splines for equidistant nodes
kj−1 + 4kj + kj+1 =
3
h
(fj+1 − fj−1)
(3) Determination of splines
pj (x) = aj0 + aj1(x − xj ) + aj2(x − xj )2
+ aj3(x − xj )3
∀ xj 5 x 5 xj+1
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-5 5 / 9

6. Continued–
(4) aj0 = pj (xj ) = fj
(5) aj1 = p0
j (xj ) = kj
(6) aj2 = 1
2p00
j (xj ) = 3
h2 (fj+1 − fj ) − 1
h (kj+1 + 2kj )
(7) aj3 = 1
6p000
j (xj ) = 2
h3 (fj − fj+1) + 1
h2 (kj+1 + kj )
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-5 6 / 9

7. Example:
Q Interpolate f (x) = x4 on the interval −1 5 x 5 1 by cubic spline
g(x) corresponding to the partition x0 = −1, x1 = 0, x2 = 1 and
satisfying the clamped conditions g0(−1) = f 0(−1), g0(1) = f 0(1)
Ans According to question
f0 = f (−1) = 1, f1 = f (0) = 0, f2 = f (1) = 1. The given interval is
partitioned into n = 2 parts and h = 1. Hence spline g consists of
n = 2 polynomial.
p0(x) = a00 + a01(x + 1) + a02(x + 1)2
+ a03(x + 1)3
− 1 5 x 5 0
p1(x) = a10 + a11x + a12x2
+ a13x3
0 5 x 5 1
Step 1: Our goal is to determine p0(x) and p1(x). Since n = 2, let j = 1 then
k0 + 4k1 + k2 =
3
1
(f2 − f0)
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-5 7 / 9

8. Continued–
Now p0
0(x0) = k0 and p0
1(x2) = k2. But g = p0 at x0 = −1 and g = p1 at
x2 = 1. Hence, as given (g0 = f 0 at ±1)
f 0
(−1) = −4 = g0
(−1) = p0
0(−1) = k0, f 0
(1) = 4 = g0
(1) = p0
1(1) = k2
Substitution of k0 = −4 and k2 = 4 ⇒ k1 = 0
Step 2: We can now obtain the coefficient of p0.
a00 = f0 = 1, a01 = k0 = −4
a02 = 3
12 (f1 − f0) − 1
1(k1 + 2k0) = 5
a03 = 2
13 (f0 − f1) + 1
12 (k1 + k0) = −2
Similarly a10 = f1 = 0, a11 = k1 = 0, a12 = −1, a13 = 2
This gives the polynomial
p0(x) = 1 − 4(x + 1) + 5(x + 1)2
− 2(x + 1)3
= −x2
− 2x3
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-5 8 / 9

9. Continued–
p1(x) = −x2
+ 2x3
or
g(x) = −x2
− 2x3
if − 1 5 x 5 0
= −x2
+ 2x3
if 0 5 x 5 1
Figure: Function f (x) = x4
and cubic spline g(x)
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-5 9 / 9