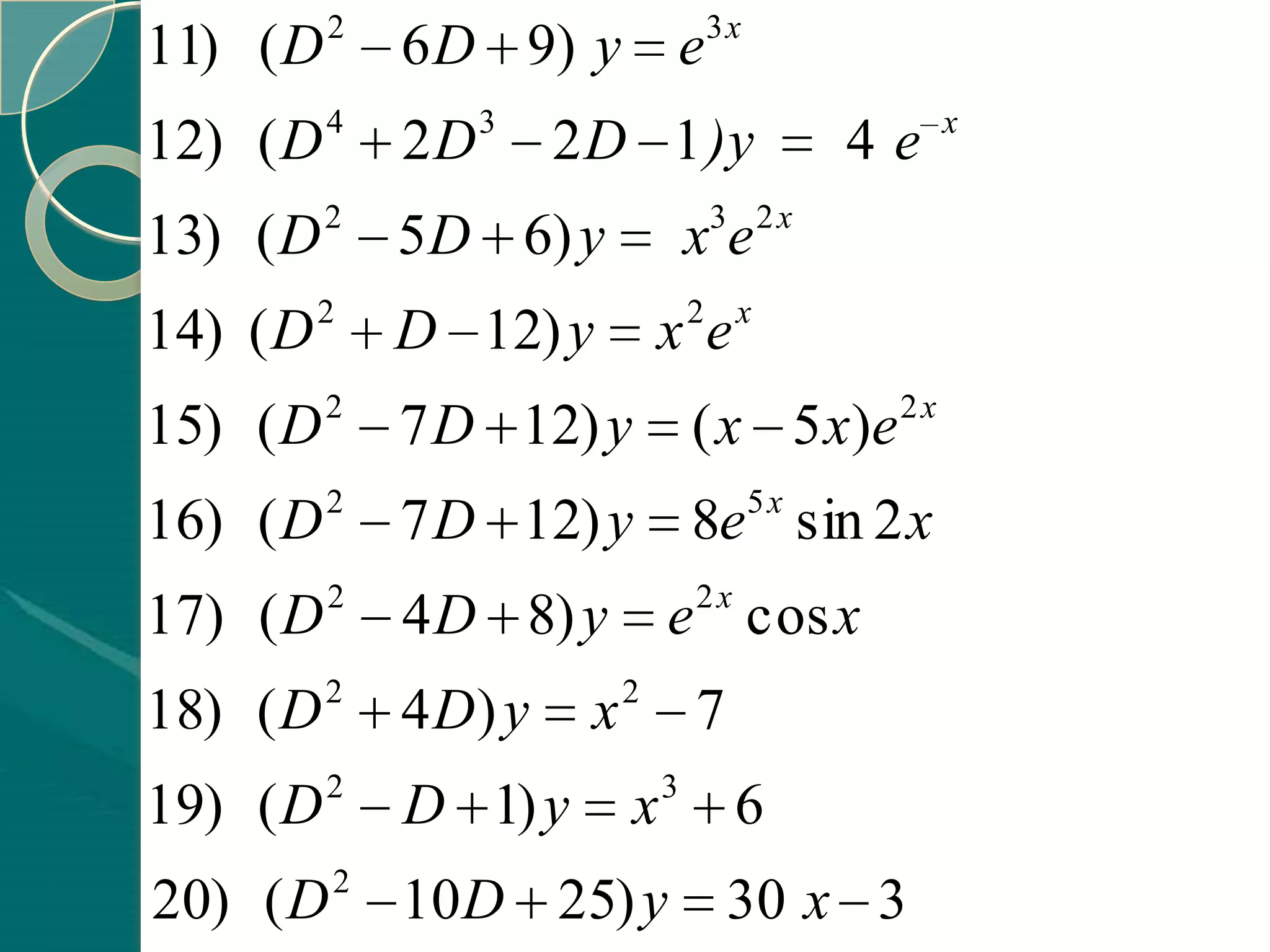1. In the Name of Allah Most Gracious Most
Merciful
Ordinary Differential
Equations
Prepared by
Ahmed Haider Ahmed
B.Sc. Physics - Dept. of Physics – Faculty of
Science

2. TO my mother , my brothers
and my best friend
Abd El-Razek

3. Preface
Differential equations are introduce in different
fields and its importance appears not only in
mathematics but also in Engineering , Natural
science ,Chemical science , Medicine ,Ecology
and Economy.
Due to its importance in different fields I collected
the laws and methods of solution of ordinary
differential equations as an introduction to study
it and to be as base to study theoretical physics
and understand the physical meaning of
relations.
LET’S UNDERSTAND
Ahmed Haider Ahmed – B.Sc. Physics

4. Definitions
Differential equation is an equation involving an
unknown function and its derivatives.
Ordinary Differential equation is differential equation
involving one independent variable and its differentials
are ordinary.
Partial Differential equation is differential equation
involving two or more independent variables and its
differentials are partial.
Order of Differential equation is the order of the highest
derivative appearing in the equation.
Degree of Differential equation is the power of highest
derivative appearing in the equation.
particular solution of a differential equation is any one
solution.
The general solution of a differential equation is the set
of all solutions.

5. Solutions of First Order Differential Equations
 1- Separable Equations
 2- Homogeneous Equation
 3- Exact Equations
 4- Linear Equations
 5- Bernoulli Equations

6. 1- Separable Equations (separation variable)
General form of differential equation is
(x ,y) dx + (x ,y) dy = 0
By separation variable
Then 1 (x) 2 (y) dx + 1(x) 2(y) dy = 0
1( x) 2 ( y)
dx dy 0
1 ( x) 2 ( y)
by integrating we find the solution of this equation.
Ex) find general solution for
xydx x 2 dy 0
1 1
dx dy by integration
x y
ln y ln x c

7. 2- Homogeneous Equation
The condition of homogeneous function is
n
f ( x , y) = f (x ,y)
and n is Homogeneous degree
(x ,y) dy + (x ,y) dx = 0
and , is Homogeneous function and have the
same degree
so the solution is
put y = xz , dy = x dz + z dx and substituting in
the last equation
the equation will be separable equation, so
separate variables and then integrate to find the
solution.

8. 3- Exact Equations
(x ,y) dy + (x ,y) dx = 0
The required condition of equation to be exact equation is
x y
and its general solution is
dx dy c
note : take repeated factor one time only.

9. if
x y
The equation will be not exact,
to convertit to be exact multiply it by integral factor
as following .
integral factor is
1
( x) exp ( y x ) dx
1
( y) exp ( x y ) dy

10. Examples
i ) (2x + 3cosy) dx + (2y – 3x siny) dy = 0
Solution
it is exact so,
(2x + 3cosy) dx = x + 3x cosy
(2y - 3x siny) dy = y + 3x cosy
The solution is
x + 3x cosy + y = c
ii) (1 – xy) dx + (xy – x ) dy = 0

11. (1 xy) ( xy x 2 )
x y 2x
x y
So, its not exact
1
Since ( x) exp ( y x ) dx
1
Then ( x) exp ( xy y ) ( x y 2 x) dx
1 1
exp x dx exp ln x exp ln x
1
(by multiplyin g this value by equation ii)
x
1
y dx ( y x)dy 0 thi equation is exact
s
x
1
x y dx ( y x)dy c
y
ln x xy c
2
note :- we took the repeated factor one time only

12. 4- Linear Equations
Linear Equation form is
dy
P( x) y Q( x)
dx
the integral factor that convert Linear Equations to
exact equation is :-
= exp p(x) dx
by multiplying integral factor by Linear Equation
form
dy
P( x) y Q( x ) his equation is exact
t
dx
so the general solution is :-
y= Q dx + c

13. dy
Ex) y y sec x cos2 x , y
dx
solution
dy
p( x) y Q( x) p( x) sec x , Q( x) cos2 x
dx
exp sec xdx exp ln sec x tan x
sec x tan x
general solution is
y Q dx c
(sec x tan x) y (sec x tan x).cos2 dx
(cos x sin x cos x)dx
1
sin x sin x c
2

14. 5- Bernoulli Equation
Bernoulli Equation form is
dy n
P( x) y Q( x) y
dx note :-
To solve Bernoulli Equation if n = 0 the
Bernoulli Equation
a) Divide Bernoulli Equation over y n will be linear
1 dy equation.
P( x) y(1 n)
Q( x)
y n dx
dz dy if n = 1 Bernoulli
b) Put z y (1 n)
then (1 n) y Equation will be
dx dx separable
1 dz equation
p( x) Q( x)
(1 n) dx
dz
(1 n) p ( x) z (1 n)Q ( x)
dx
this is linear equation and its solution as w e told before.

15. dy y2
Ex) y – 3 sin x
dx x
solution
dy y
– 3 sin x. y 1
dx x
dz dy
put z y andthen 2y
dx dx
dz z
2 6 sin x thisequation is linear
dx x
exp pdx exp 2
x dx exp 2 ln x exp ln x 2
x2
the general solution will be
x2 y 6 x 2 sin xdx c
x2 y 6 ( x 2 cos x sin x cos x) c

16. Solution of 1st order and high degree
differential equation :-
 1- Acceptable solution on p.
 2- Acceptable solution on y.
 3- Acceptable solution on x.
 4- Lagrange’s Equation.
 5- Clairaut’s Equation.
 6- Linear homogeneous differential
Equations with Constant Coefficients.
 7- Linear non-homogeneous differential
Equations with Constant Coefficients.

17. 1- Acceptable solution on p
if we can analysis the equation then the equation
will be acceptable solution on p
Ex) x 2 p 2 3 xpy 2 y2 0
Sol
xp y xp 2y 0
xp y 0 or xp 2y 0
dy dy
x y 0 or x 2y 0
dx dx
dy dx dy dx
or 2
y x y x
ln y ln x ln c1 or ln y 2 ln x ln c2
xy c1 0 or x2 y c2 0
( xy c1 )( x 2 y c2 ) 0
and this is the general solution of the equation.

18. 2- Acceptable solution on
y
If we can not analysis the equation then the
equation will be acceptable solution on y
or x
firstly , to solve the equation that acceptable solution on y
there are three steps :-
1- Let y be in term alone .
2- By differentiation the equation with respect to x
and solve the differential equation .
3- By deleting p from two equations (the origin
equation and the equation that we got after second
step) if we can not delete it the solution called
the parametric solution .

19. p2 dy
Ex) 3y 2 px 2 , p
x dx
Solution
2 2 p2
y px by differentiation with respect tox
3 3 x
dy 2 dp 2 1 dp 2 p2
p x 2p
dx 3 dx 3 x dx 3 x2
1 2 p2 2 4 p dp
p x , multiplyin g by 3
3 3 x2 3 3 x dx
p2 p dp
p 2 2 2 x 2 , multiplyin g by x 2
x x dx

20. 2 2 3 dp
px 2 p 2( x 2 px)
dx
dp
p( x 2 2 p) 2 x( x 2 2 p)
dx
2 dp
( x 2 p) p 2 x 0
dx
dp
x2 2 p 0 or p 2x 0
dx
dp dp
2 x2 p 2x
dx dx
2 dp dx
2dy x dx
p 2x
x3 1
2y c ln p ln x p x
3 2
to delete p from two equation substituting about p on origin equation
1 3
y x
6

21. 3- Acceptable solution on x
secondly, to solve the equation that acceptable solution on
x
there are three steps :-
1- Let x be in term alone .
2- By differentiation the equation with respect
to y and solve the differential equation .
3- By deleting p from the two equations (the
origin
equation and the equation that we got after second
step
if we can not delete it the solution called the

22. dy
Ex) x p p3 , p
dx
by differentiation with respect toy
dx dp 2 dp 1 dx
3p , but
dy dy dy p dy
1 2 dp
(1 3 p )
p dy
dp 1
dy p (1 3 p 2 )
dy ( p 3 p 3 )dp
1 2 3 4
y p p
2 4
x p p3 (the origin equation)
we can not delete p from the last tow equations so
this the parametric solution.

23. 4- Lagrange’s
Equation
Lagrange’s Equation form
y = x g (p) + f (p)
Ex) y 2 xp p
dy dp dp
2 p 2x 2p
dx dx dx Note
dp dp the method of solution
p 2 p(2 x 2 p) p (2 x 2 p) in the example
dx dx
2x dp dx 2x
1 ( 2) 2
p dx dp p
dx 2 x
2 linear differential equation
dp p
dp
exp 2 integral factor
p
e 2 ln p p2 p2 x 2 p 2 dp
2 2 p3
p x c
3

24. 5- Clairaut’s Equation
Clairaut’s Equation is special case of Lagrange’s
Equation
Clairaut’s Equation form :-
y = x p + f (p)
a Note
Ex) y px
p the method of solution
in the example
dy dp a dp
p x
dx dx p 2 dx
a dp
p p x
p 2 dx
a dp
x 0
p dx
dp a
0 o
r (x 2
) 0
dx p

25. a
p c & p
x
a
y xc
c
2 a2 a
y p2 x2 2 2 px
p p
a2
y2 p 2 x2 2ax , 2
y a ax 2ax
p2
y2 4ax single solution (parabola)

26. 6 - Linear homogeneous Differential Equations with
Constant Coefficients
(a0 D n a1 D n 1
a2 D n 2
........ an ) y f ( x)
d
D , a0 , a1 , a2 , a3 ,..... n are constant
a
dx
L(D) y = f (x) non-homogeneous
but L(D) y = 0 homogeneous
then L( ) = 0 assistant equation
Roots of this equation are 1 , 2 , 3 ,……, n
This roots take different forms as following:-

27. 1- if roots are real and different each other then the
complement solution is
1x 2x nx
yc C1e C2 e ......... Cn e
2- if roots are real and equal each other then
complement solution is
x r 1
yc e (C1 C2 x ......... Cn x )
3- if roots are imaginary then complement solution is
x
yc e (C1 cos x C2 sin x )

28. examples
:-
1) y y 0 3)( y a ) y 0
(D3 D) y 0 (D 2
a )y 2
0
3 2
( ) 0 ( 1) 0 2 2
( a ) 0
( 1)( 1) 0
1 0, 2 1, 3 1 ai
yc C1 C2 e x
C3 e x yc C1 cos ax C2 sin ax
2) y 3y 2y 0 4)(D 2 2 D 2) y 0
( D 2 3 D 2) y 0
( 1)( 2 1) 0
( 3 2) 0
1 1, 2 i
( 1)( 2) 0
x
1, 2 yc C1e C2 cos x C3 sin x
1 2
x 2x
yc C1e C2 e

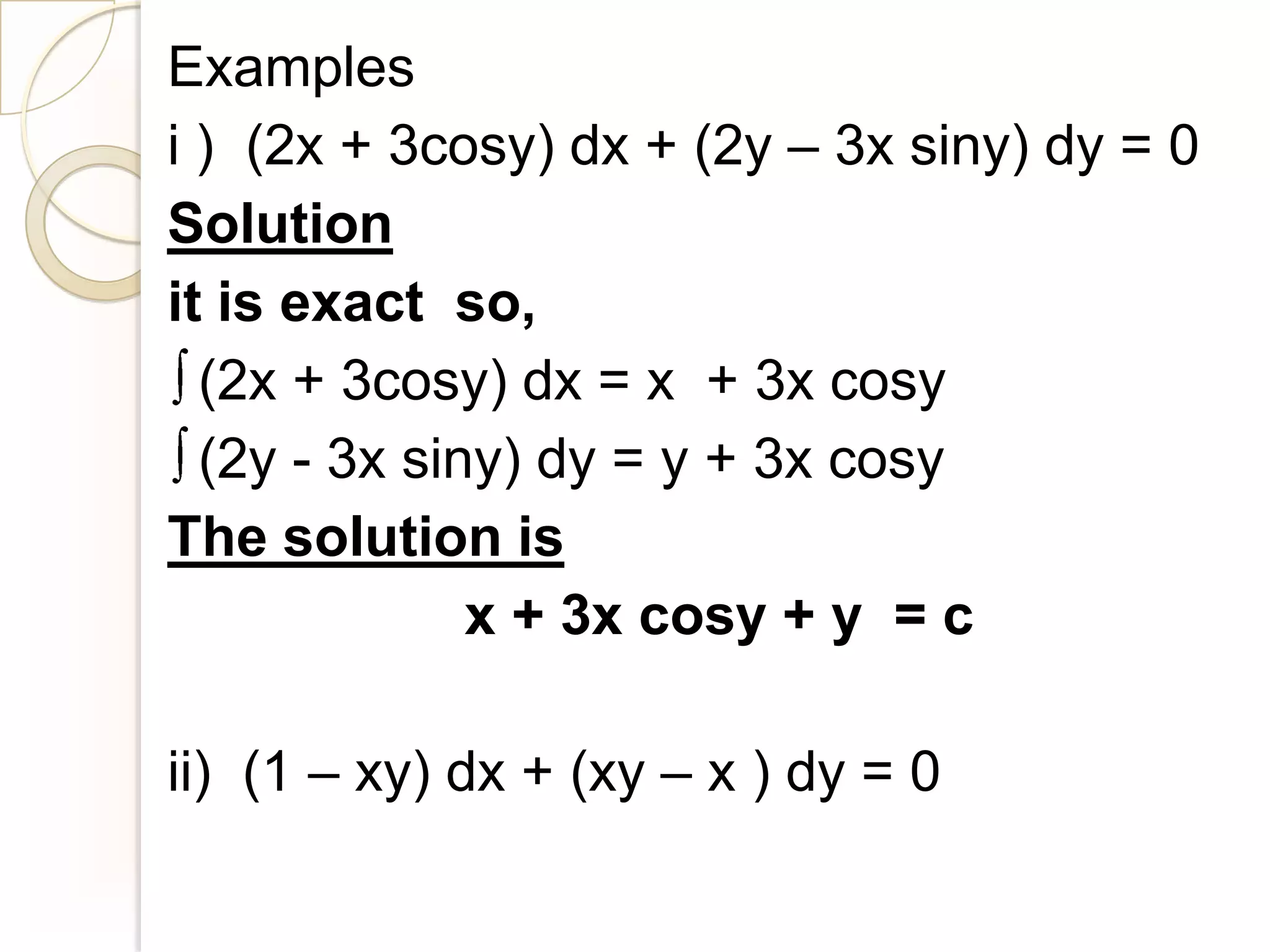
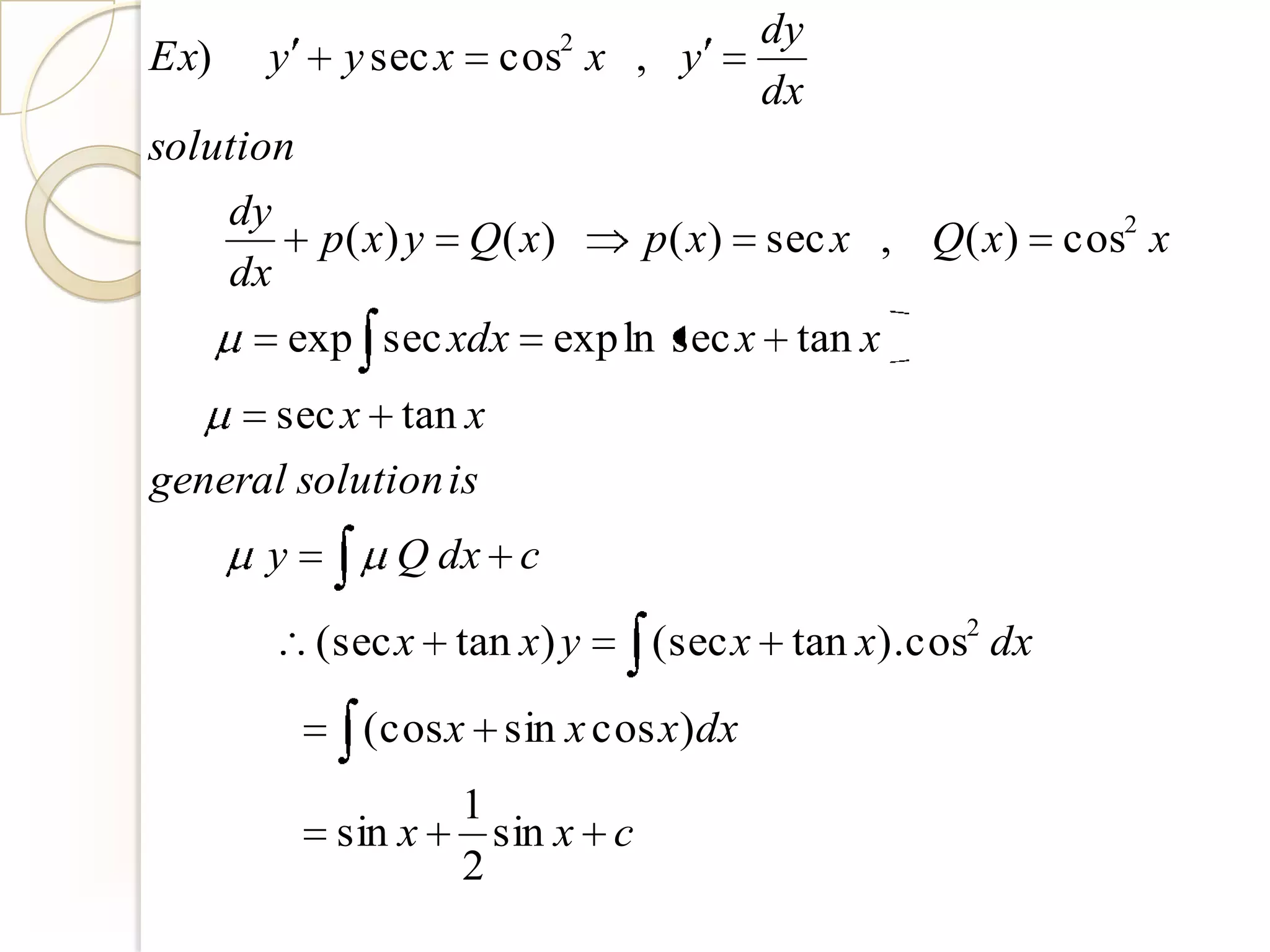
29. 7- Linear non-homogeneous Differential Equations with
Constant Coefficients
L(D) y = f (x) non-homogeneous
the general solution of non-homogeneous is
y = yc + yp
yc complement solution
[solution of homogeneous equation L(D) y = 0 look last slide]
y p particular solution is Note
L(D) is differential
1 effective
y f ( x) 1 / L(D) is integral
L( D) effective
We knew how to get the complement
solution last slide. To get the particular solution it depends on the type
of function we will know the different types and example to every
one as following .

30. 1
Particular solution is y f ( x)
L( D)
i) if f (x) is exponential function
1 e ax
y e ax ; L(a) 0 ; D a
L( D) L(a )
ii) special case in exponential function at L (a) = 0
1 e ax
y e ax
L( D) L( D a )
iii) if exponential function multiplied f(x)
1 1
y f ( x)e ax e ax f ( x)
L( D ) L( D a )
iv) if f (x) is trigonometric function sin x or cos x
1 1
y 2
sin ax or cos ax 2
sin ax or cos ax
L( D ) L( a )

31. v) if f (x) is trigonometric function sin x or cos x multiplied
exponential function
1 1
y e ax sin x or cos x e ax sin x or cos x
L( D) L( D a )
vi ) If f (x) is polynomial
L( D) f ( x)
1
y f ( x)
L( D)
and then use partial fractions or use the following series : -
1
(1 - x) 1 x x2 x3 ..
1
(1 x) 1 x x2 x3

32. solved example :-
y y 6 y 8e3 x
(D2 D 6) y 0
2
6 0
2 3 0
1 2 , 2 3
yc C1e 2 x C2 e 3x
1 1
yp 2
8e3 x yp 8e3 x
D D 6 9 3 6
D a
8 3x 4 3x
yp e e
6 3
general solution y yc yp
2x 3x 4 3x
y C1 e C2 e e
3

33. general problems
1) ( xy 2 y )dx ( x 2 y x)dy 0
2) (2 xy tan y )dx ( x 2 sec2 y )dy 0
3) (e x 4 y )dx (4 x sin y )dy 0
4) ( x 2 y 2 ) dx xy dy 0
dx
5) y y 2 ln x
dy
dy
6) 3 2 y y 4e3 x
dx
7) y x p p 2
x
8) y p
p
9) y y 4 y 4 y 0
10) y 2y - 8y 0

34. 2 3x
11) ( D 6 D 9) y e
4 3 x
12) ( D 2D 2 D 1 )y 4e
13) ( D 2 5 D 6) y x3 e 2 x
2 2 x
14) ( D D 12) y xe
15) ( D 2 7 D 12) y ( x 5 x )e 2 x
2 5x
16) ( D 7 D 12) y 8e sin 2 x
17) ( D 2 4 D 8) y e 2 x cos x
2 2
18) ( D 4 D) y x 7
19) ( D 2 D 1) y x3 6
2
20) ( D 10 D 25) y 30 x 3

35.  
Finally , this course of ordinary differential equations is
useful
to different student special students of physics.
Theoretical
physics required to be know the bases of mathematics
specially differential equations such that quantum
mechanics
depend on Schrödinger equation and this equation is
differential equation so this branch of physics depend
upon
differential equations . I made slide of problems in
different
types of differential equations to examine yourself .
Finally don’t forget these words for Napoleon “the
advancing
and perfecting of mathematics are closely related by
prosperity of the nation”

36. Ahmed Haider Ahmed
Nuclear Physics Lab
Faculty of Science
Minia university
Minia City
Egypt