Downloaded 11 times
Uploaded byDeep Dalsania
Gauss Forward And Backward Central Difference Interpolation Formula
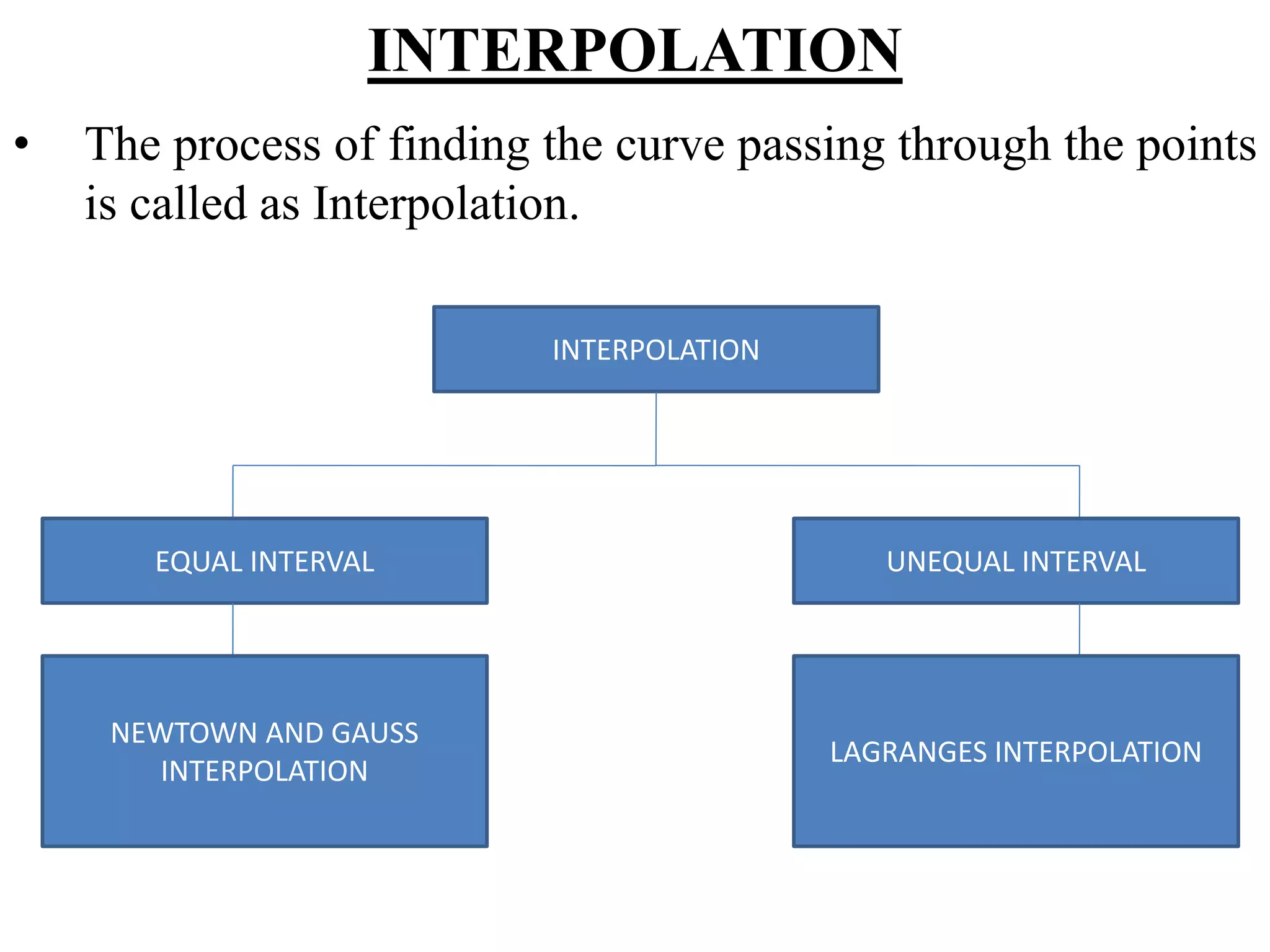
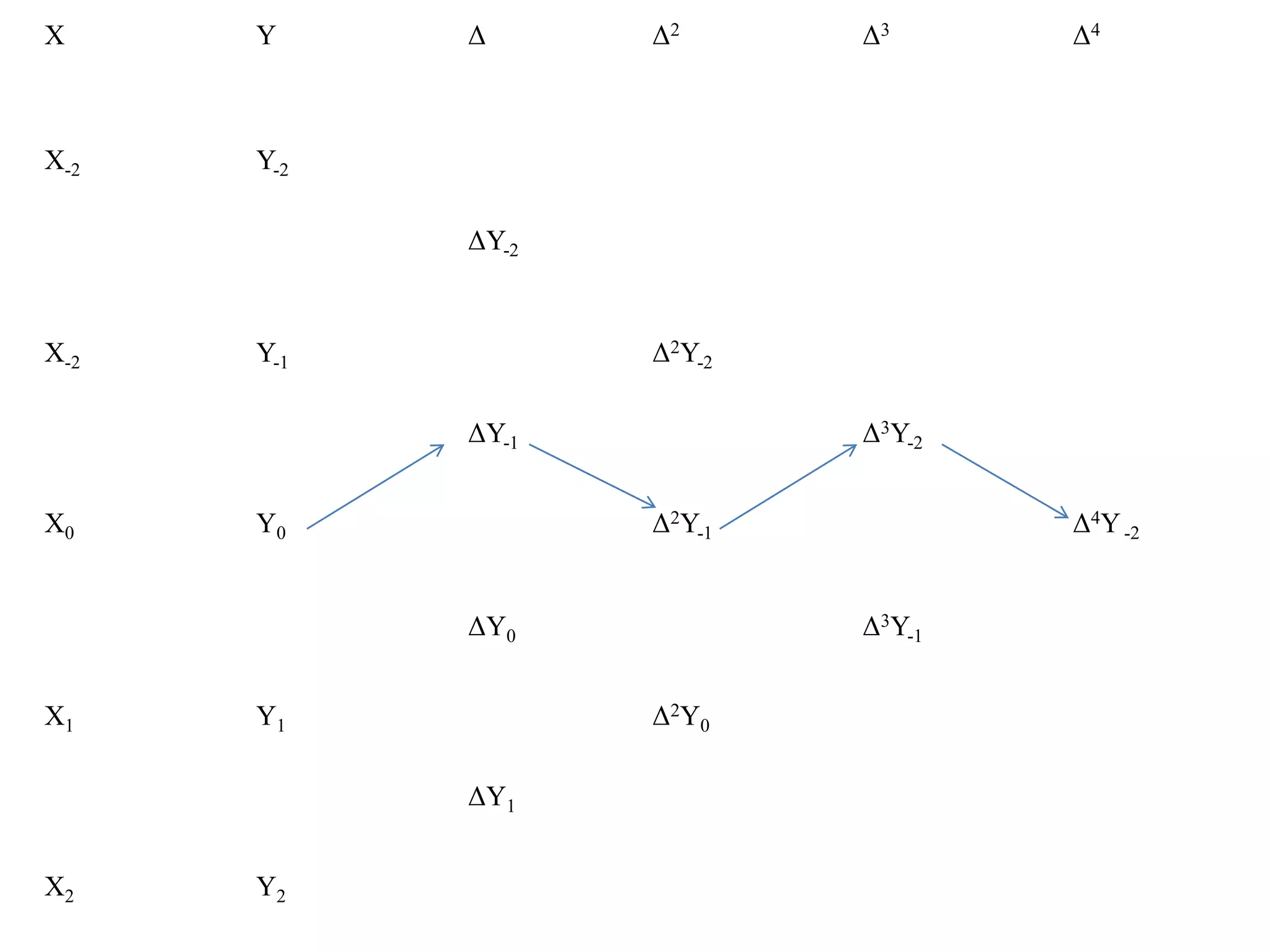
The presentation covers Gauss forward and backward central difference interpolation formulas, focusing on how to find curves passing through given points. It discusses different types of interpolation including equal and unequal intervals, as well as Newton and Lagrange methods. The presentation is part of a numerical and statistical methods course for computer engineering.
More Related Content
Similar to Gauss Forward And Backward Central Difference Interpolation Formula
Gauss Forward And Backward Central Difference Interpolation Formula
- 1. Presentation on Gauss ForwardAnd Backward Central Difference Interpolation Formula Presented By : • Deep Dalsania (160350116002) • Jhanvi Ghediya (160350116003) • Rakesh Talaviya (160350116010) • Drashti Bangoriya (160350116001) • Bhakti Tank (160350116011) • Subject Name: Numerical and Statistical Methods For Computer Engineering • Subject Code: 2140706 • Submitted To: Prof. Dipesh Bhogayata Sir
- 2. INTERPOLATION • The processof finding the curve passing through the points is called as Interpolation. INTERPOLATION EQUAL INTERVAL UNEQUAL INTERVAL NEWTOWN AND GAUSS INTERPOLATION LAGRANGES INTERPOLATION
- 3. Gauss Forward CentralDifference Formula
- 4. X Y ΔΔ2 Δ3 Δ4 X-2 Y-2 ΔY-2 X-2 Y-1 Δ2Y-2 ΔY-1 Δ3Y-2 X0 Y0 Δ2Y-1 Δ4Y-2 ΔY0 Δ3Y-1 X1 Y1 Δ2Y0 ΔY1 X2 Y2
- 5. Gauss Backward CentralDifference Formula
- 6. X Y ΔΔ2 Δ3 Δ4 X-2 Y-2 ΔY-2 X-2 Y-1 Δ2Y-2 ΔY-1 Δ3Y-2 X0 Y0 Δ2Y-1 Δ4Y-2 ΔY0 Δ3Y-1 X1 Y1 Δ2Y0 ΔY1 X2 Y2