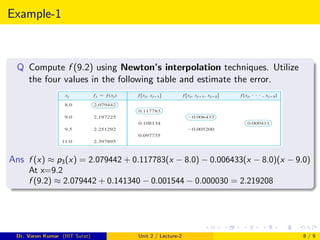
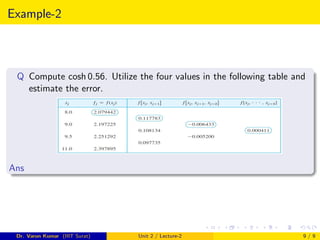
1. Newton's divided difference interpolation is a method for interpolating or finding function values between given data points. It involves constructing polynomials that pass through the given points. 2. The method works by first constructing lower degree Newton polynomials that fit the existing data points, then adding higher degree terms to fit additional points. These terms involve divided differences of the function values at the data points. 3. The general Newton interpolation formula expresses the interpolating polynomial as a sum of terms, with each term being a product of divided differences and factors corresponding to the distances between the interpolated point and data points.

1. Newton’s Divided Difference Interpolation
Dr. Varun Kumar
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-2 1 / 9

2. Outlines
1 Introduction to Newton’s Divide Difference Interpolation
2 Example
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-2 2 / 9

3. Introduction to Newton’s Divide Difference Interpolation
Important points
⇒ Interpolation means to find values of a function f (x) for an x
between different x− values x0, x1, ....., xn at which the values of f (x)
are given. Mathematically
f0 = f (x0), f1 = f (x1), .... fn = f (xn)
⇒ Lagrange’s formulation is useful for deriving formulas in numeric
integration and differentiation.
⇒ Newton’s forms is more practical that can also be used for solving
ordinary differential equations (ODEs).
⇒ They involve fewer arithmetic operations than Lagranges form.
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-2 3 / 9

4. Newton’s Formulation
⇒ Let pn−1(x) be the (n − 1)th Newton’s polynomial thus
pn−1(x0) = f0, pn−1(x1) = f1, ...., pn−1(xn−1) = fn−1. Let the nth
Newton’s polynomial is
pn(x) = pn−1(x) + gn(x) (1)
or
gn(x) = pn(x) − pn−1(x) (2)
⇒ Here gn(x) is determined, so that pn(x0) = f0, pn(x1) = f1, ....,
pn(xn) = fn
⇒ pn and pn−1 are same for x0, x1, ...., xn−1
⇒ gn(x) must be of the form
gn(x) = an(x − x0)(x − x1)....(x − xn−1) (3)
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-2 4 / 9

5. Continued–
⇒ Using (3), let x = xn
an =
fn − pn−1(xn−1)
(xn − x0)(xn − x1)....(xn − xn−1)
⇒ We write ak instead of an and show that ak equals to the kth divided
difference, recursively.
a1 = f [x0, x1] =
f1 − f0
x1 − x0
a2 = f [x0, x1, x2] =
f [x1, x2] − f [x0, x1]
x2 − x0
ak = f [x0, ...., xk] =
f [x1, x2, .., xk] − f [x0, ..xk−1]
xk − x0
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-2 5 / 9

6. Continued–
⇒ If n = 1, then pn−1(xn) = p0(x1) = f0 because p0(x) is constant.
Hence from (3)
a1 =
f1 − p0(x1)
x1 − x0
=
f1 − f0
x1 − x0
= f [x0, x1]
⇒ Hence Newton’s interpolation for the first degree
p1(x) = f0 + (x − x0)f [x0, x1]
⇒ If n = 2, then pn−1(xn) = p1(x2). Hence from (3)
a2 =
f2 − p1(x2)
(x2 − x1)(x2 − x0)
=
f2 − f0 − (x2 − x0)f [x0, x1]
(x2 − x1)(x2 − x0)
= f [x0, x1, x2]
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-2 6 / 9

7. Continued–
⇒ We thus obtain the second Newton’s polynomial
p2(x) = f0 + (x − x0)f [x0, x1] + (x − x0)(x − x1)f [x0, x1, x2]
⇒ For n = k, we can write
pk(x) = pk−1(x) + (x − x0)(x − x1)....(x − xk−1)f [x0....xk]
⇒ The more generalized Newton’s divide and difference
interpolation formula can be expressed as
f (x)= f0 + (x − x0)f [x0, x1] + (x − x0)(x − x1)f [x0, x1, x2] + ...+
= (x − x0)(x − x1)....(x − xn−1)f [x0, ..., xn]
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-2 7 / 9

8. Example-1
Q Compute f (9.2) using Newton’s interpolation techniques. Utilize
the four values in the following table and estimate the error.
Ans f (x) ≈ p3(x) = 2.079442 + 0.117783(x − 8.0) − 0.006433(x − 8.0)(x − 9.0)
At x=9.2
f (9.2) ≈ 2.079442 + 0.141340 − 0.001544 − 0.000030 = 2.219208
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-2 8 / 9

9. Example-2
Q Compute cosh 0.56. Utilize the four values in the following table and
estimate the error.
Ans
Dr. Varun Kumar (IIIT Surat) Unit 2 / Lecture-2 9 / 9