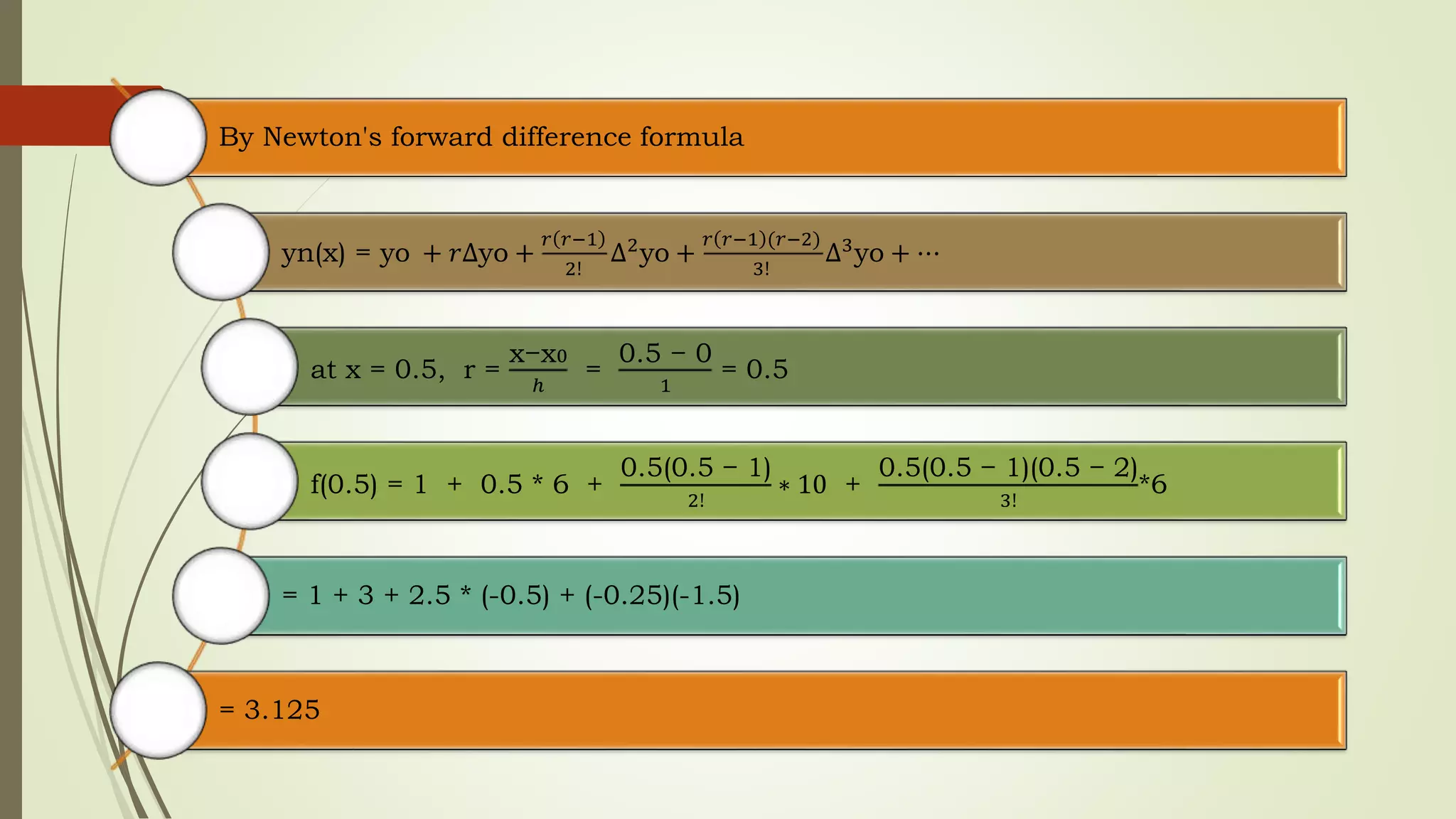
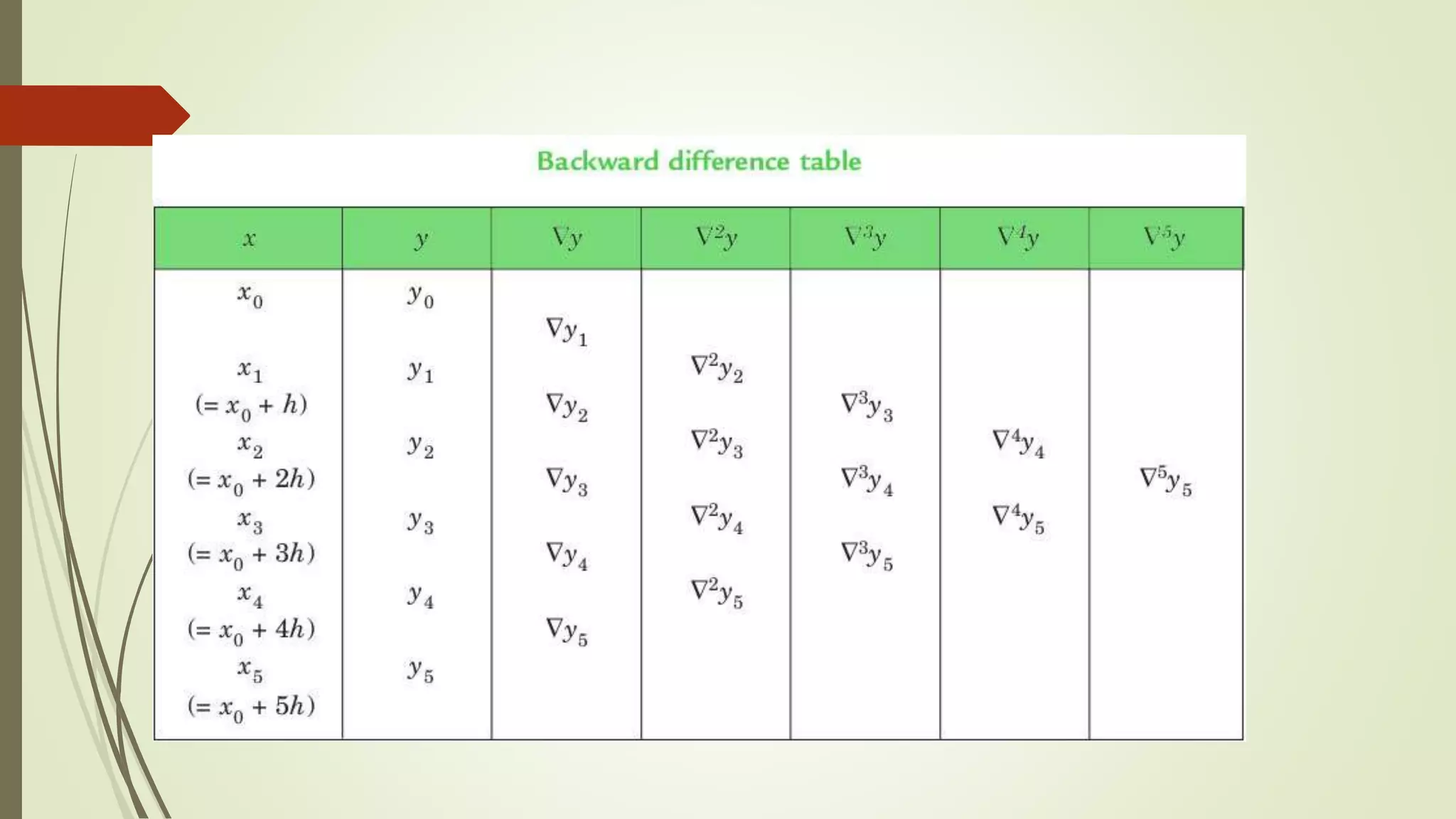
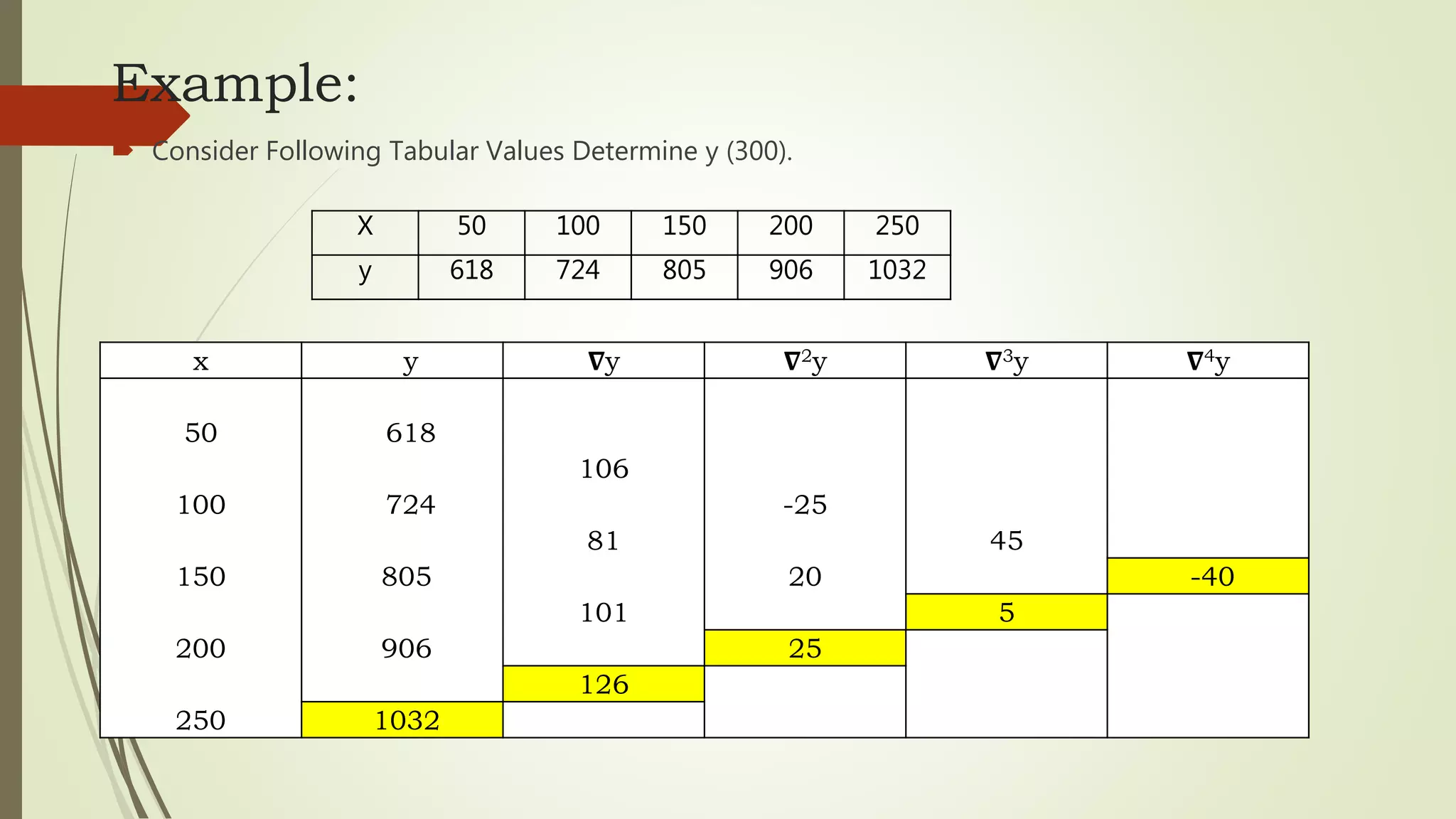
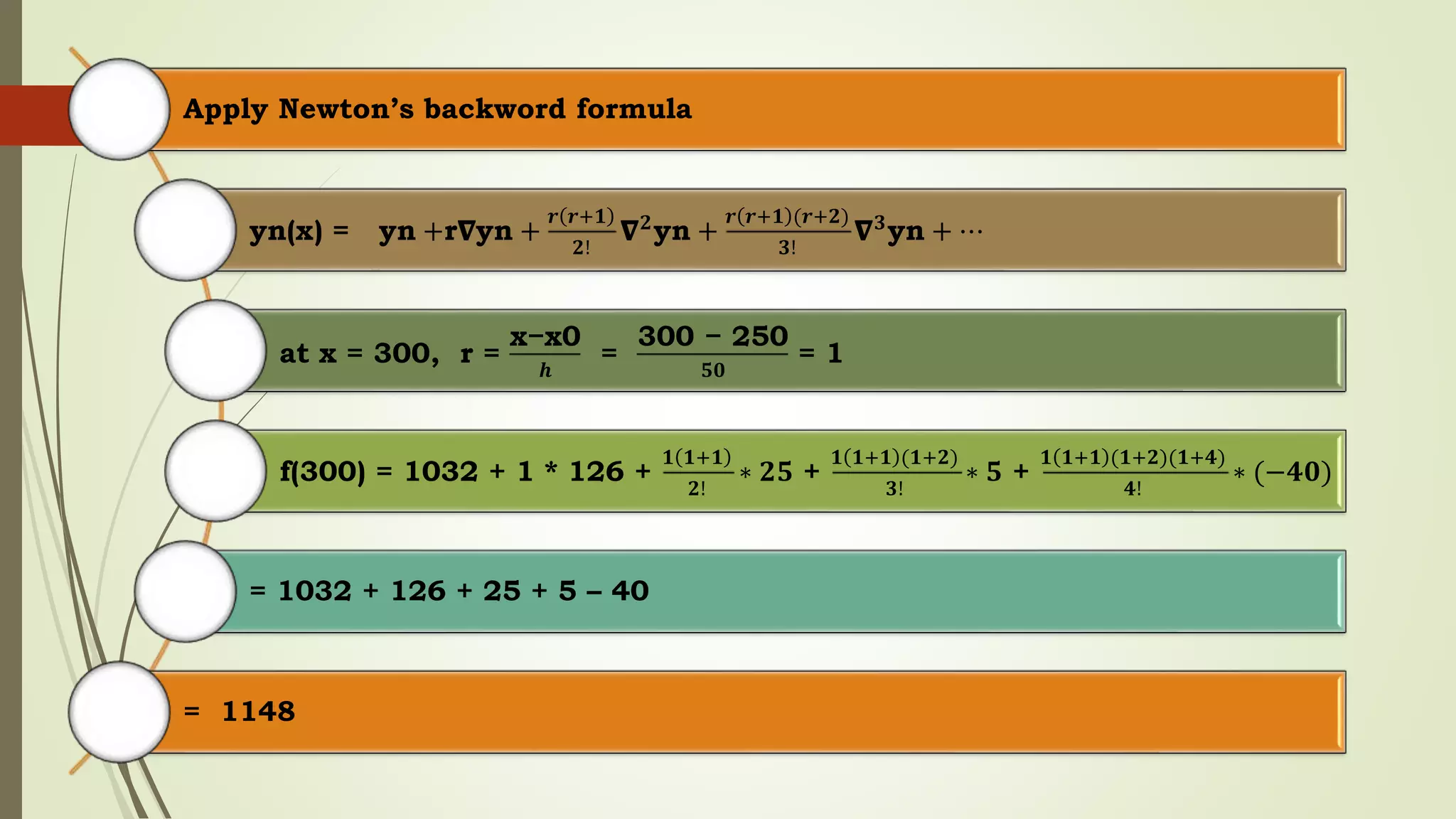
Newton's forward and backward interpolation are methods for estimating the value of a function between known data points. Newton's forward interpolation uses a formula to calculate successive differences between the y-values of known x-values to estimate y-values for unknown x-values greater than the last known x-value. Newton's backward interpolation similarly uses differences but to estimate y-values for unknown x-values less than the first known x-value. The document provides an example of using Newton's forward formula to find the estimated y-value of 0.5 given a table of x and y pairs, calculating the differences and plugging into the formula. It also works through an example of Newton's backward interpolation to estimate the y-value at

1. Prepared By: Harshad Koshti
NSM (2140706)
Newton’s Forward & Backword
Interpolation

2. Interpolation
Let the function y=f(x) take the values y0, y1,y2,…,yn corresponding
to the values x0,x1,x2,…,xn of x. The process of finding the value of y
corresponding to any value of x=xi between x0 and xn is called
interpolation.

3. Newton’s Forward Interpolation
 Let the function y=f(x) take the values y0,y1,y2,…,yn corresponding to the
values x0,x1,x2,…,xn of x. Suppose it is required to evaluate f(x) for x=x0 + rh ,
where r is any real number.
 Formula :
Yn (x) = yo + 𝑟∆yo +
𝑟 𝑟−1
2!
∆2yo +
𝑟 𝑟−1 (𝑟−2)
3!
∆3yo + ⋯
where r =
x−x0
ℎ

4. Newton’s Forward Interpolation
x y Dy D2y D3y D4y D5y
x0 y0
Dy0 = y1- y0
x1 y1 D2y0 = Dy1- Dy0
Dy1 = y2 - y1 D3y0 = D2y1- D2y0
x2 y2 D2y1 = Dy2 - Dy1 D4y0 = D3y1- D3y0
Dy2 = y3 - y2 D3y1 = D2y2 - D2y1 D5y0 = D4y1- D4y0
x3 y3 D2y2 = Dy3 - Dy2 D4y1 = D3y2 - D3y1
Dy3 = y4 - y3 D3y2 = D2y3 - D2y2
x4 y4 D2y3 = Dy4 - Dy3
Dy4 = y5 - y4
x5 y5

5. Example: If f(x) is known at the following data points then
find f(0.5) using Newton's forward difference formula.
xi 0 1 2 3 4
fi 1 7 23 55 109
x fi Dfi D2fi D3fi D4fi
0 1
6
1 7 10
16 6
2 23 16 0
32 6
3 55 22
54
4 109

6. By Newton's forward difference formula
yn(x) = yo + 𝑟∆yo +
𝑟 𝑟−1
2!
∆2yo +
𝑟 𝑟−1 (𝑟−2)
3!
∆3yo + ⋯
at x = 0.5, r =
x−x0
ℎ
=
0.5 − 0
1
= 0.5
f(0.5) = 1 + 0.5 * 6 +
0.5(0.5 − 1)
2!
∗ 10 +
0.5(0.5 − 1)(0.5 − 2)
3!
*6
= 1 + 3 + 2.5 * (-0.5) + (-0.25)(-1.5)
= 3.125

7. Newton’s Backword Interpolation
 Let the function y=f(x) take the values y0,y1,y2,…,yn
corresponding to the values x0,x1,x2,…,xn of x. Suppose it is
required to evaluate f(x) for x=x0 + r*h , where r is any real
number.
 Formula :
 yn(x) = yn +rસyn +
𝑟 𝑟+1
2!
સ2
yn +
𝑟 𝑟+1 (𝑟+2)
3!
સ3
yn + ⋯
where r =
x−xn
ℎ

9. Example:
 Consider Following Tabular Values Determine y (300).
X 50 100 150 200 250
y 618 724 805 906 1032
x y સy સ2y સ3y સ4y
50 618
106
100 724 -25
81 45
150 805 20 -40
101 5
200 906 25
126
250 1032

10. Apply Newton’s backword formula
yn(x) = yn +rસyn +
𝒓 𝒓+𝟏
𝟐!
સ 𝟐
yn +
𝒓 𝒓+𝟏 (𝒓+𝟐)
𝟑!
સ 𝟑
yn + ⋯
at x = 300, r =
x−x0
𝒉
=
300 − 250
𝟓𝟎
= 1
f(300) = 1032 + 1 * 126 +
𝟏 𝟏+𝟏
𝟐!
∗ 𝟐𝟓 +
𝟏 𝟏+𝟏 (𝟏+𝟐)
𝟑!
∗ 𝟓 +
𝟏 𝟏+𝟏 (𝟏+𝟐)(𝟏+𝟒)
𝟒!
∗ (−𝟒𝟎)
= 1032 + 126 + 25 + 5 – 40
= 1148