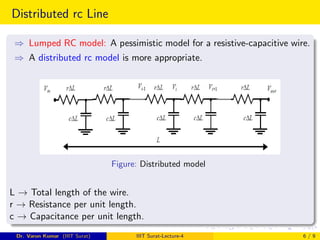
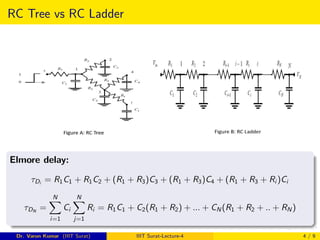
This document discusses and compares lumped RC and distributed RC models. It describes: 1) Lumped RC models treat a wire as a single resistor and capacitor in series, which is inaccurate for long wires. Distributed RC models account for resistance and capacitance per unit length. 2) Distributed RC lines can be modeled by RC trees or RC ladders, where Elmore delay formulas are derived. 3) Delay and time constant in a distributed RC line increase quadratically with wire length, whereas lumped RC models overestimate this relationship. 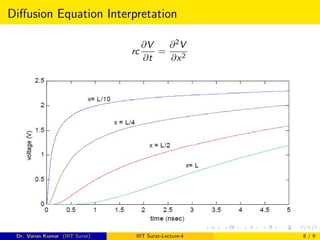4) The behavior of a distributed RC line is described by a diffusion equation relating voltage, distance, resistance, and capacitance over time.

1. Distributed rc Model
Dr. Varun Kumar
Dr. Varun Kumar (IIIT Surat) IIIT Surat-Lecture-4 1 / 9

2. Outlines
1 Lumped RC Model vs Distributed rc Model
2 RC Tree vs RC Ladder
3 Effect of Length of Wire on Delay and Time Constant
4 Distributed rc Line
Dr. Varun Kumar (IIIT Surat) IIIT Surat-Lecture-4 2 / 9

3. Lumped RC Model vs Distributed rc Model
⇒ The equipotential assumption in the lumped-capacitor model is no
longer adequate.
⇒ A resistive-capacitive model has to be adopted.
⇒ Approach for analysis (Short wire)
Lumps the total wire resistance of each wire segment into one single R
Combines the global capacitance into a single capacitor C
This simple model, called the lumped RC model
Note: Inaccurate for long interconnect wires.
⇒ Challenges and approach for analysis (Long wire)
The distributed rc-model is complex and no closed form solutions exist.
The distributed rc-line can be adequately modeled by a simple RC
network.
Dr. Varun Kumar (IIIT Surat) IIIT Surat-Lecture-4 3 / 9

4. RC Tree vs RC Ladder
Elmore delay:
τDi
= R1C1 + R1C2 + (R1 + R3)C3 + (R1 + R3)C4 + (R1 + R3 + Ri )Ci
τDN
=
N
X
i=1
Ci
N
X
j=1
Ri = R1C1 + C2(R1 + R2) + ... + CN (R1 + R2 + .. + RN )
Dr. Varun Kumar (IIIT Surat) IIIT Surat-Lecture-4 4 / 9

5. Effect of Length of Wire on Delay and Time Constant
⇒ τ = RC → (Time constant) → Simple RC network.
⇒ τ → Time required to charge 0 to 63.2% of the value on applied DC
voltage and discharge to 36.8% from its initial value.
Effect of length of wire:
⇒ Let RC ladder model is taken and R1 = R2 = ...RN = R
⇒ The wire with a total length is L.
⇒ It is partitioned into N parts.
⇒ Resistance and capacitance per unit length, i.e r = R
N and c = C
N .
⇒ Overall delay
τDN
=
L
N
2
(rc + 2rc + ... + Nrc) =
N + 1
2N
L2
rc
Note: The delay of in distributed rc-line is half of the delay in lumped RC
model.
Dr. Varun Kumar (IIIT Surat) IIIT Surat-Lecture-4 5 / 9

6. Distributed rc Line
⇒ Lumped RC model: A pessimistic model for a resistive-capacitive wire.
⇒ A distributed rc model is more appropriate.
Figure: Distributed model
L → Total length of the wire.
r → Resistance per unit length.
c → Capacitance per unit length.
Dr. Varun Kumar (IIIT Surat) IIIT Surat-Lecture-4 6 / 9

7. Continued–
Figure: Schematic symbol for distributed RC line
c∆L
∂Vi
∂t
=
(Vi+1 − Vi ) − (Vi − Vi−1)
r∆L
The correct behavior of the distributed rc line is obtained by reducing ∆L → 0.
Diffusion equation:
rc
∂V
∂t
=
∂2V
∂x2
⇒ V → Voltage at a particular point in the wire
⇒ x → Distance between reference point and the signal source.
Dr. Varun Kumar (IIIT Surat) IIIT Surat-Lecture-4 7 / 9

8. Diffusion Equation Interpretation
rc
∂V
∂t
=
∂2V
∂x2
Dr. Varun Kumar (IIIT Surat) IIIT Surat-Lecture-4 8 / 9

9. Comparison between Lumped RC
⇒ No closed-form solution exists for this equation.
⇒ These equations are difficult to use for ordinary circuit analysis.
⇒ Distributed rc line can be approximated by a lumped RC ladder network.
Dr. Varun Kumar (IIIT Surat) IIIT Surat-Lecture-4 9 / 9