The circuit remains in state S0/10. Edge-triggered behavior means the circuit only responds to transitions of the clock signal, not its level. Since the clock did not transition from 0 to 1, the circuit ignores the changes to D and remains in the same state.

1. Feedback Sequential Circuits
• The simplest bistable / latches /
flipflops are all FSCs
• Each has one or more feedback loops
• Ignoring the behavior during
transitions they store a 0 or 1 at all
times
• The feedback loops are memory
elements and the circuits behavior
depends on both the current inputs
and the values stored in the loops

2. Analysis
• FSCs are the most common example
of Fundamental mode circuits.
– Inputs are not normally allowed to
change simultaneously.
– Analysis procedure assumes inputs
change one at a time
– Circuit settles to a stable internal state
• Differs from clocked circuits, in
which multiple inputs can change at
almost arbitrary times without
affecting the state and all input
values are sampled and state changes
occur with respect to a clock signal
• Feedback sequential circuits may be
Mealy or Moore circuits.
• A circuit with n feedback loops has n
binary state variables and 2n states.

3. FSC structure for Mealy and
Moore machines
Mealy
machine
only
Inputs
Next Output
State
Current state Logic
Logic F G
Outputs
Feedback loops

4. • Break the feedback loops so that the next
value stored in each loop can be
predicted as a function of the circuit
inputs and the current value stored in all
loops.
• Insert a fictional buffer whose output is Y
• Y is the single state variable in this
example
• If current state Y and inputs C and D are
known the next state Y* can be predicted

5. Excitation equation
Y* = (C D ) + (C D’ + Y’)’
Y* = C D + C’ Y + D Y
• Now the state of the feedback loop can be
written as a function of the current state
and input
Transition table
• Each cell in the transition table shows the
output of the fictional buffer after the
corresponding state and input combination
occurs

6. • By definition, a fundamental–mode
circuit does not have a clock to tell it
when to sample its inputs.
• Instead we can imagine that the circuit is
evaluating its current state continuously
• As a result of each evaluation, it goes into
the next state predicted by the transition
table
• Most of the time, the next state is the
same as the current state; this is the
essence of the fundamental –mode
operation

7. Some definitions
• Total state: combination of internal state (value
of feedback loop) and input state (current input
value) .
• Stable total state: Total state whose next state
predicted by the state table is the same as the
current internal state.
• Unstable total state: Total state whose next state
predicted by the state table is different from the
current internal state.
State table
State Input CD
S 00 01 11 10
S0 S0 S0 S1 S0
S1 S1 S1 S1 S0
Next State S*

8. • To complete the analysis, we must
determine how the outputs behave as
functions of the internal state and inputs.
• There are two outputs and hence two
equations
Q = Y* = C D + C’ Y + D Y
QN = C D’ + Y’
•Note that Q and QN are outputs, not state
variables.
•Even though the circuit has two outputs
which can take up 4 combinations, it has
only 1 state variable Y, and hence only 2
states
•The output values can be incorporated in a
combined state/output table which
completely describes the circuit

9. State output table
•Although Q and QN are normally
complimentary, it is possible for them to
have the same value momentarily
•They have the value 1 momentarily during
the transition from S0 to S1 under the input
combination CD = 11
•The behavior of the circuit can be
predicted from this state output table

10. Analysis for few transitions
• Start with stable total state “S0/00” ( S =
S0 and CD = 00)
• 1 bit changes at a time
• Change D to 1
• Change C to 1

11. Multiple input changes
• Start with stable total state “S1/11”
• C and D are both simultaneously set to 0
• Almost simultaneous input changes occur
in practice
• May change in different orders
• -suppose C changes first, final is S1/00
• -suppose D changes first, final is S0/00
• Unpredictable final state, feedback loop
may become metastable

12. Multiple input changes
• Start with stable total state “S0/00”
• C and D are both simultaneously set to 1
• Almost simultaneous input changes occur
in practice
• May change in different orders
• -suppose C changes first, final is S1/11
• -suppose D changes first, final is S1/11
• Simultaneous input changes don’t always
cause unpredictable behavior.

13. Analyzing Circuits with Multiple
Feedback Loops
• Break each loop and insert buffers
• Many possible ways – cut sets
• Best? Minimal cut set
• Different minimal cut sets
• Different excitation equations, transition
tables and state/output tables
• However, stable total states derived from
one set should correspond one-to-one to
the stable total states from the other
• State/Output table should give the same
input/output behavior, with only the
names and coding of the states changed
• Even if non minimal cut sets are used the
resulting state/output table will still
describe the circuit correctly but using
more states

14. Analyzing Circuits with Multiple
Feedback Loops
• A good example is the commercial circuit
design for a positive edge triggered TTL
D flip-flop
• The circuit is simplified assuming that
the Preset and Clear inputs are never
asserted and showing the fictional buffers
to break the 3 feedback loops

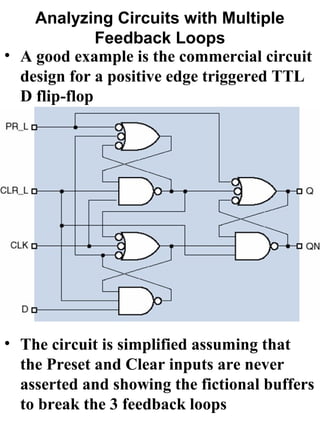
15. Simplified Positive Edge triggered
D flip-flop for analysis
(Y2·D)+(Y1·C)
Y1*
{[(Y2·D)+(Y1·C)+C‘]·Y3}+(Y1·C)
Y1
(Y1·C)'
Y3*
(Y2·D)+(Y1·C)+C' Y3
Y2*
Y2 {[(Y2·D)+(Y1·C)+C‘]·Y3}'
(Y2·D)'
Y1* = (Y2·D)+(Y1·C)
Y2* = (Y2·D)+(Y1·C)+C' = (Y2·D)+(Y1)+C'
Y3* = {[(Y2·D)+(Y1·C)+C']·Y3}+(Y1·C)
= {[(Y2·D)+(Y1)+C']·Y3}+(Y1·C)
= (Y2·Y3·D)+(Y1·Y3)+(C‘·Y3)+(Y1·C)

16. Simplified Positive Edge triggered
D flip-flop for analysis
(Y2·D)+(Y1·C)
Y1*
{[(Y2·D)+(Y1·C)+C‘]·Y3}+(Y1·C)
Y1
(Y1·C)'
Y3*
(Y2·D)+(Y1·C)+C' Y3
Y2*
Y2 {[(Y2·D)+(Y1·C)+C‘]·Y3}'
Y2·D'
Q = Y3* = (Y2·Y3·D)+(Y1·Y3)+(C‘·Y3)+(Y1·C)
QN = {[(Y2·D)+(Y1·C)+C']·Y3}'
= [(Y2·D)+(Y1)+C']'+Y3'
= [(Y2·D)'· (Y1)'·C'']+Y3'
= [(Y2'+D')·(Y1)'·C]+Y3'
= (Y2'·Y1'·C) + (D'·Y1'·C)+Y3'

17. Transition table

18. Races
• A race is said to occur when multiple internal
variables change state as a result of a single
input changing state.
• Starting at state 011/00 change CLK to 1.
• The next internal state is 000
• The state may change as 011→ 010→ 000
• Or as 011→ 001→ 000

19. • Noncritical race: the final state does not depend
on the order in which the state variables change.
• Now modifying the next state entry for total
state 010/10 to 110 instead of 000
• The state may change as 011→ 010→ 110 → 111
• Or as 011→ 001→ 000
• The next internal state could be111 or 000
• Critical race: the final state depends on the
order in which the state variables change.
110

20. State Tables
• Once it has been determined that a
transition table does not have any critical
races, the state-variable combinations can
be named and outputs can be determined
to obtain a state/output table.
• State table shows that it takes multiple
hops to reach a new stable total state in
some cases
• S0/11→S2/01→S6/01

21. Flow Tables
Flow table eliminates:
– Rows for unused internal states (states
that are stable for no input
combination).
– Next state entries for total states that
cannot be reached from a stable total
state as the result of a single input
change.
• It eliminates multiple hops and shows
only the ultimate destination of each
transition.

22. State Table to Flow table

23. Flow table
01

24. Edge triggered behavior
• Assume internal state S0/10.
• Change D to 1, then 0.
• Change clock to 0.
• Change D to 1, then 0.
• What happens when clock changes
to 1.