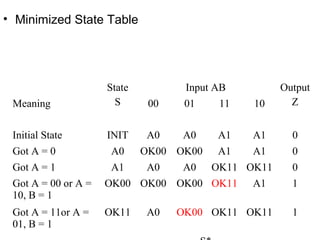
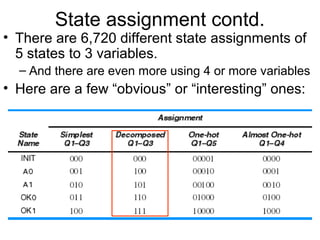
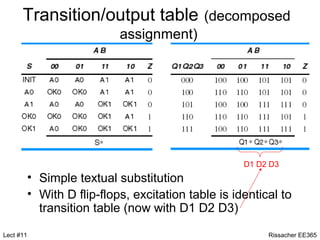
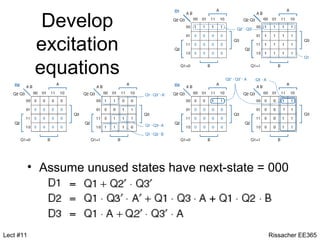
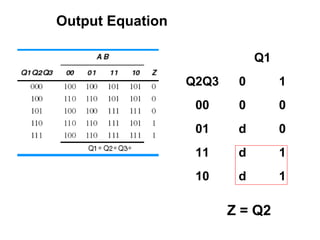
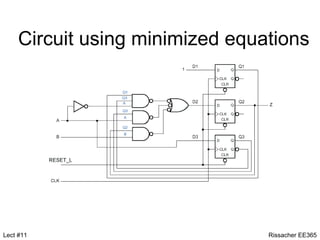
This document discusses state machine design using state diagrams and state tables. It provides examples of designing a state machine with inputs A and B and output Z. Key steps include: 1. Defining the machine's states and behaviors in a state table. 2. Assigning state codes to minimize the number of variables needed. 3. Deriving excitation and output equations from the state table. 4. Implementing the state machine design using flip-flops and combinational logic.

1. State-machine design and synthesis
The creative part, like Turning the crank, like
writing a program a compiler does

2. Designing State Machines Using State
Diagrams
• State-diagram design is simpler but it is more prone to
errors.
– State table is an exhaustive listing of the next states for
each state/input combination. No ambiguity is possible.
– When constructing a state diagram there is no guarantee
that the transition expressions written on the arcs leaving
a particular state, cover all input combination exactly
once.

3. Designing State Machines Using State
Diagrams
• Mutual exclusion: For each state the logical product of each
pair of transition expression on arcs leaving that state
should be zero. If there are n arcs then there are n(n-1)/2
logical products to evaluate
• All inclusion: For each state the logical sum of the transition
expressions on all arcs leaving the state should be one.
• A state table guarantees mutual exclusion and all inclusion
• A state diagram needs to be verified for mutual exclusion
and all inclusion so that there is no ambiguity.

4. • Design a machine with inputs A and B, and output Z
that is 1 if:
– A had the same value at the two previous ticks
– B has been 1 since the last time the above was true
State Input AB Output
Meaning S 00 01 11 10 Z
Initial State INIT A0 A0 A1 A1 0
Got A = 0 A0 OK00 OK00 A1 A1 0
Got A = 1 A1 A0 A0 OK11 OK11 0
Got A = 00 OK00 OK00 OK00 OK01 A1 1
Got A = 11 OK11 A0 OK10 OK11 OK11 1
Got A = 01, B = 1 OK01 A0 OK10 OK11 OK11 1
Got A = 10, B = 1 OK10 OK00 OK00 OK01 A1 1

5. • Minimized State Table
State Input AB Output
Meaning S 00 01 11 10 Z
Initial State INIT A0 A0 A1 A1 0
Got A = 0 A0 OK00 OK00 A1 A1 0
Got A = 1 A1 A0 A0 OK11 OK11 0
Got A = 00 or A = OK00 OK00 OK00 OK11 A1 1
10, B = 1
Got A = 11or A = OK11 A0 OK00 OK11 OK11 1
01, B = 1

6. State Assignment
• Can minimize number of states (see text), but
hardly anyone bothers anymore.
• Need to assign state-variable combinations to
states.
– Minimum number of variables for n states is log2
n
Example -- 4 states, 2 state variables (Q1,Q2):
A ==> 00
B ==> 01
C ==> 10
D ==> 11 Up to this point is “art”, the
rest is just “turning the crank.”
Lect #11 Rissacher EE365

7. State assignment contd.
• The design example has 5 states, so
minimum f/fs required are 3
• For 3 f/fs we have 8 states and we
require only 5
• Hence there will be 3 unused states
• Two approaches
-Minimal Risk
-Minimal Cost

8. Minimal Risk
• All unused states are identified and explicit next
state entries are made so that, for any input
combination the unused states will go to the
‘initial’, ‘idle’ or ‘safe’ state
Minimal Cost
• All unused states are identified and next state
entries are marked as ‘don’t cares’. In most
cases this simplifies the excitation logic.
However, the machine’s behavior if it enters an
unused state may be pretty weird

9. Guidelines for state assignments
• Choose an initial coded state into which the
machine can easily be forced at reset (00.. Or
11..)
• Minimize the number of state variables that
change on each transition
• Maximize the number of state variables that do
not change in a group of related states. ( a
group of states in which most of the transitions
stay in the group)

10. Guidelines for state assignments
• Exploit symmetries in the problem specification
and the corresponding symmetries in the state
table.
• If there are unused states then use the ‘best’
available states
• Decompose the set of states into individual bits
or fields, where they have a well defined
meaning with respect to the input effects or
output behavior
• Consider more than the minimum number of
state variables

11. State assignment contd.
• There are 6,720 different state assignments of
5 states to 3 variables.
– And there are even more using 4 or more variables
• Here are a few “obvious” or “interesting” ones:

12. One–hot assignment
• It uses 1 bit per state
• Simple
• Each f/f needs to be set to ‘1’ for transitions in
only one state
• More number of f/fs
• Usually used for a machine with S states that is
required to have a set of 1 out-of-S coded
outputs indicating its current state. The one-hot
-coded f/f outputs can be used directly for this
purpose, with no additional combinational
output logic

13. Almost One–hot assignment
• It uses a ‘no-hot’ combination for the initial state
Reasons
-Easy to initialize most storage devices to 0
-Initial state in particular is usually not visited
once the machine gets going

14. Incorporation of some guidelines
• Initial state is 000 which is easy to force using
Reset signal
• Q1 is used to indicate whether the machine is
in INIT state or not
-Q1 = 0 implies INIT state
-Q1 = 1 implies non-INIT states
• Q2 indicates that the conditions for a ‘1’ output
are satisfied in the current state.
-Q2 = 0 for A0, A1 states
-Q2 = 1 for OK0, OK1 states

15. Incorporation of some guidelines
• Q3 indicates the previous value of A.
-Q3 = 0 for OK0, A0 states
-Q3 = 1 for OK1, A1 states
• By decomposing the state bits meanings in this
way, we can expect the next state and output
logic to be simpler than in a ‘random’
assignment

16. Transition/output table (decomposed
assignment)
D1 D2 D3
• Simple textual substitution
• With D flip-flops, excitation table is identical to
transition table (now with D1 D2 D3)
Lect #11 Rissacher EE365

17. Develop
excitation
equations
• Assume unused states have next-state = 000
Lect #11 Rissacher EE365

18. Option:
Minimize
with “Don’t
Cares”
D1 = 1
D2 = Q1 • Q3´ • A´ + Q3 • A + Q2 • B
D3 = A
Lect #11 Rissacher EE365

19. Output Equation
Q1
Q2Q3 0 1
00 0 0
01 d 0
11 d 1
10 d 1
Z = Q2

20. Circuit using minimized equations
Lect #11 Rissacher EE365