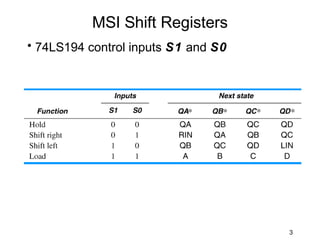
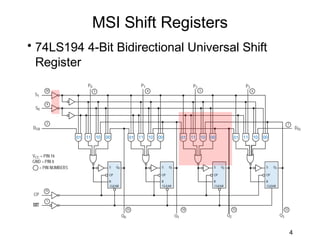
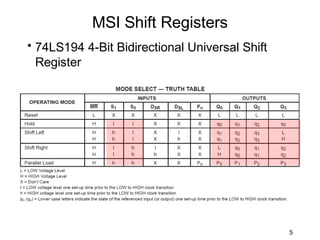
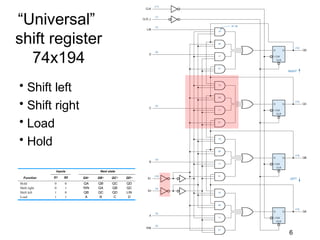
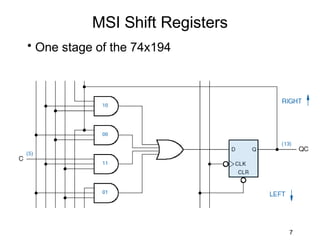
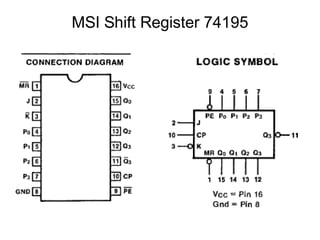
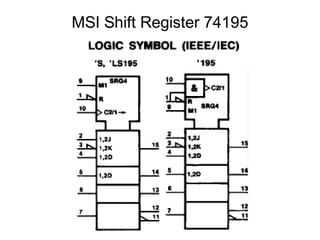
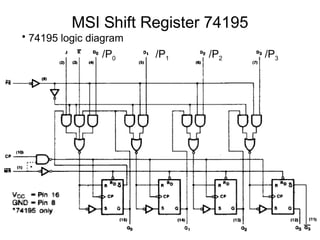
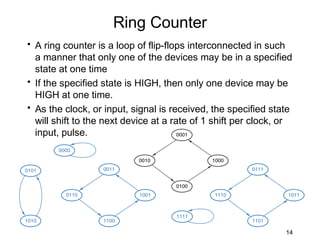
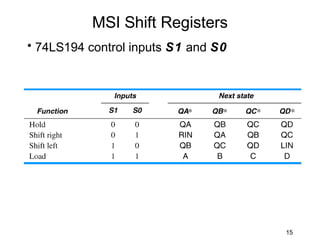
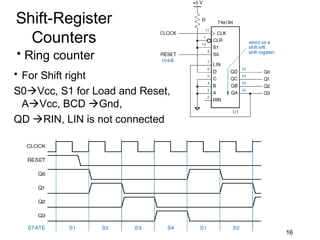
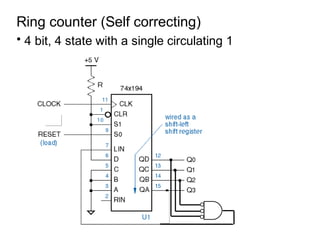
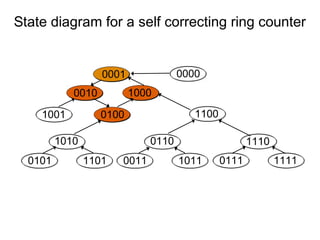
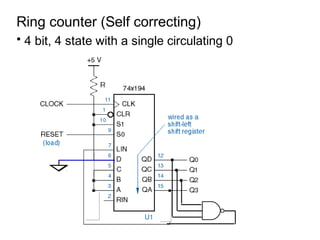
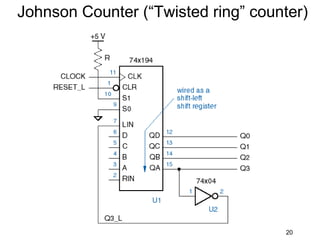
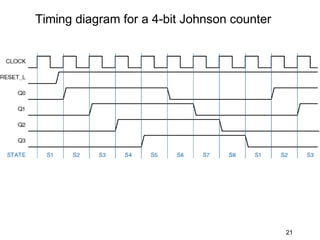
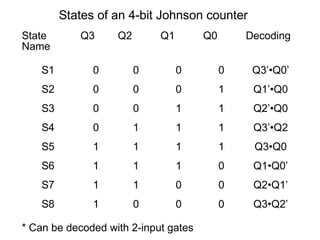
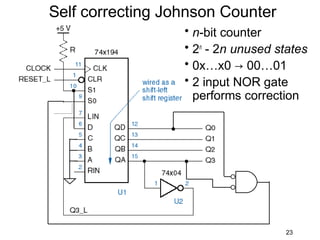
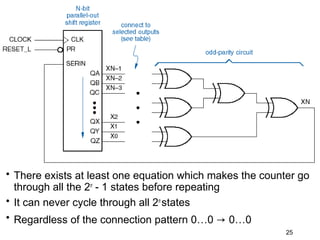
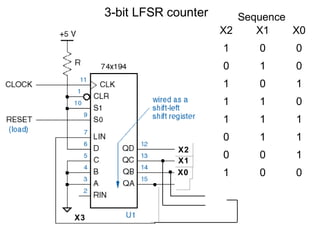
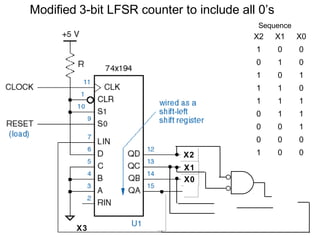
The document discusses various types of shift registers including the 74LS194 4-bit bidirectional universal shift register which can perform shift left, shift right, serial-serial, serial-parallel, parallel-serial, and parallel-parallel transfers. It also describes ring counters, Johnson counters, and linear feedback shift register (LFSR) counters. LFSR counters can cycle through all possible 2^n-1 states using feedback connections to determine the state sequence.

1. MSI Shift Registers
• 74LS194 4-Bit
Bidirectional Universal
Shift Register
• may be used in the
following data register
transfers
– serial-serial,
– shift left,
– shift right,
– serial-parallel,
– parallel-serial,
– and parallel-parallel
1

2. MSI Shift Registers
• 74LS194 4-Bit Bidirectional Universal Shift
Register
2

3. MSI Shift Registers
• 74LS194 control inputs S1 and S0
3

4. MSI Shift Registers
• 74LS194 4-Bit Bidirectional Universal Shift
Register
01 11 10 00 01 11 10 00 01 11 10 00 01 11 10 00
4

5. MSI Shift Registers
• 74LS194 4-Bit Bidirectional Universal Shift
Register
5

6. “Universal”
shift register
74x194
• Shift left
• Shift right
• Load
• Hold
6

7. MSI Shift Registers
• One stage of the 74x194
7

9. MSI Shift Register 74195

10. MSI Shift Register 74195

11. MSI Shift Register 74195
or D0–D3

12. MSI Shift Register 74195

13. MSI Shift Register 74195
• 74195 logic diagram
/P0 /P1 /P2 /P3

14. Ring Counter
• A ring counter is a loop of flip-flops interconnected in such
a manner that only one of the devices may be in a specified
state at one time
• If the specified state is HIGH, then only one device may be
HIGH at one time.
• As the clock, or input, signal is received, the specified state
will shift to the next device at a rate of 1 shift per clock, or
input, pulse.
14

15. MSI Shift Registers
• 74LS194 control inputs S1 and S0
15

16. Shift-Register
Counters
• Ring counter
• For Shift right
S0Vcc, S1 for Load and Reset,
AVcc, BCD Gnd,
QD RIN, LIN is not connected
16

17. Ring counter (Self correcting)
• 4 bit, 4 state with a single circulating 1

18. State diagram for a self correcting ring counter
0001 0000
0010 1000
1001 0100 1100
1010 0110 1110
0101 1101 0011 1011 0111 1111

19. Ring counter (Self correcting)
• 4 bit, 4 state with a single circulating 0

20. Johnson Counter (“Twisted ring” counter)
20

21. Timing diagram for a 4-bit Johnson counter
21

22. States of an 4-bit Johnson counter
State Q3 Q2 Q1 Q0 Decoding
Name
S1 0 0 0 0 Q3’•Q0’
S2 0 0 0 1 Q1’•Q0
S3 0 0 1 1 Q2’•Q0
S4 0 1 1 1 Q3’•Q2
S5 1 1 1 1 Q3•Q0
S6 1 1 1 0 Q1•Q0’
S7 1 1 0 0 Q2•Q1’
S8 1 0 0 0 Q3•Q2’
* Can be decoded with 2-input gates

23. Self correcting Johnson Counter
• n-bit counter
• 2n - 2n unused states
• 0x…x0 → 00…01
• 2 input NOR gate
performs correction
23

24. Linear Feedback Shift Register Counter
• n-bit shift register counters have far less than the
maximum number of 2n normal states
• n states for ring counter, 2n states for Johnson counter
• An n-bit LFSR counter can have 2n – 1 states
also called as maximum length sequence generator
• Design is based on the theory of finite fields
• Developed by French mathematician Evariste Galois
• Serial input is connected to the sum modulo 2 of a
certain set of output bits
• These feedback connections determine the state
sequence of the counter
• By convention, outputs are always numbered and
shifted in the direction shown in figure on next slide

25. • There exists at least one equation which makes the counter go
through all the 2n - 1 states before repeating
• It can never cycle through all 2n states
• Regardless of the connection pattern 0…0 → 0…0
25

26. Feedback
equations
for LFSR
counters
26

27. 3-bit LFSR counter Sequence
X2 X1 X0
1 0 0
0 1 0
1 0 1
1 1 0
1 1 1
0 1 1
X2
X1
0 0 1
X0 1 0 0
X3

28. Modified LFSR Counter
• An LFSR can be modified to have 2n states including the
all 0’s state
• In an n-bit LFSR counter, an extra EXOR gate and an n
– 1 input NOR gate connected to all the shift register
outputs except X0 accomplishes the task
• The states are not visited in binary order
• Usually used where this characteristic is an advantage
- Generating test inputs for logic circuits
- Encoding and decoding circuits for certain error-
detecting and error-correcting codes including
CRC codes
- Scrambling and descrambling data patterns in data
communications
- Pseudo random binary sequence generator

29. Modified 3-bit LFSR counter to include all 0’s
Sequence
X2 X1 X0
1 0 0
0 1 0
1 0 1
1 1 0
1 1 1
0 1 1
0 0 1
0 0 0
X2 1 0 0
X1
X0
X3