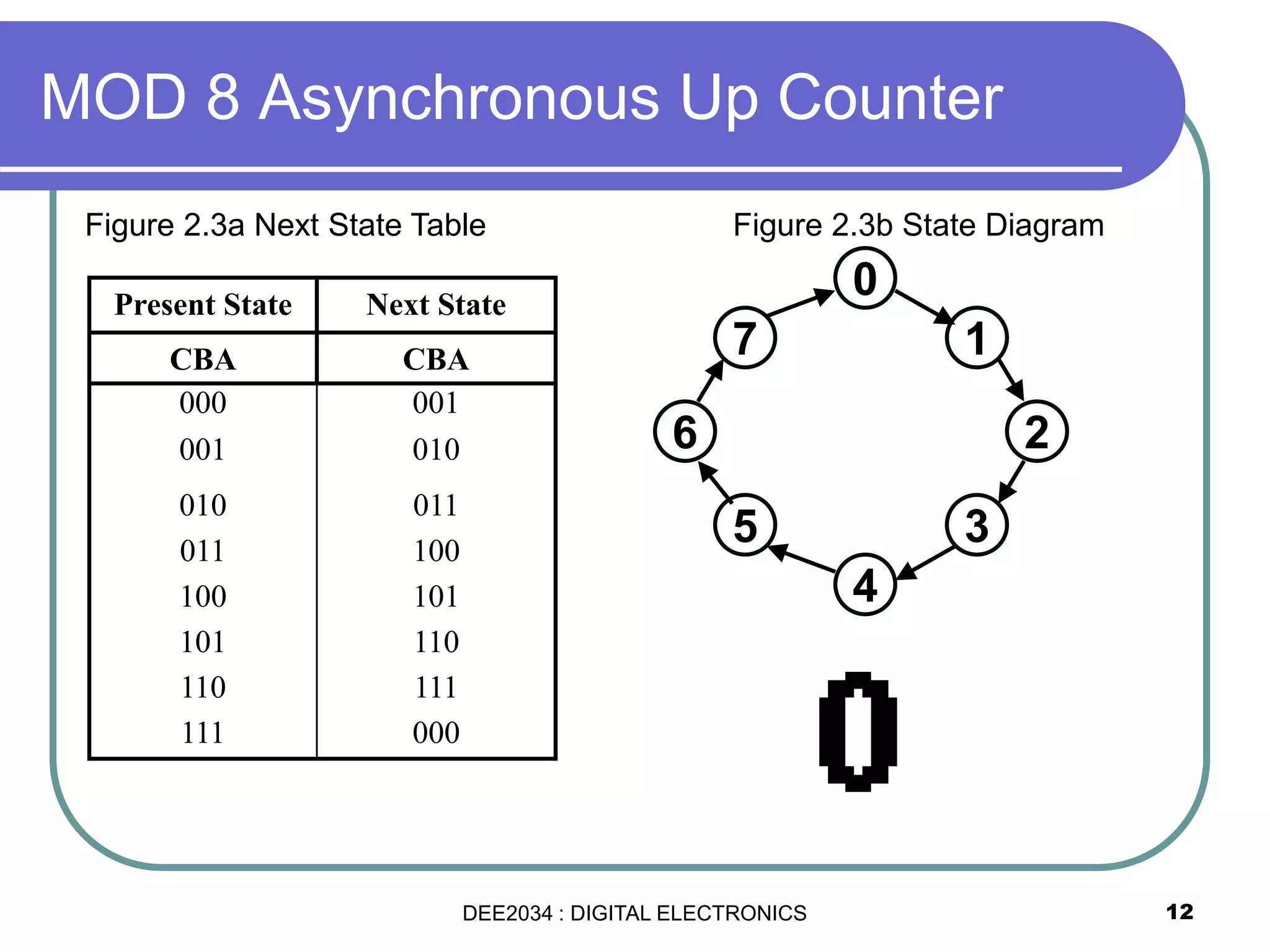
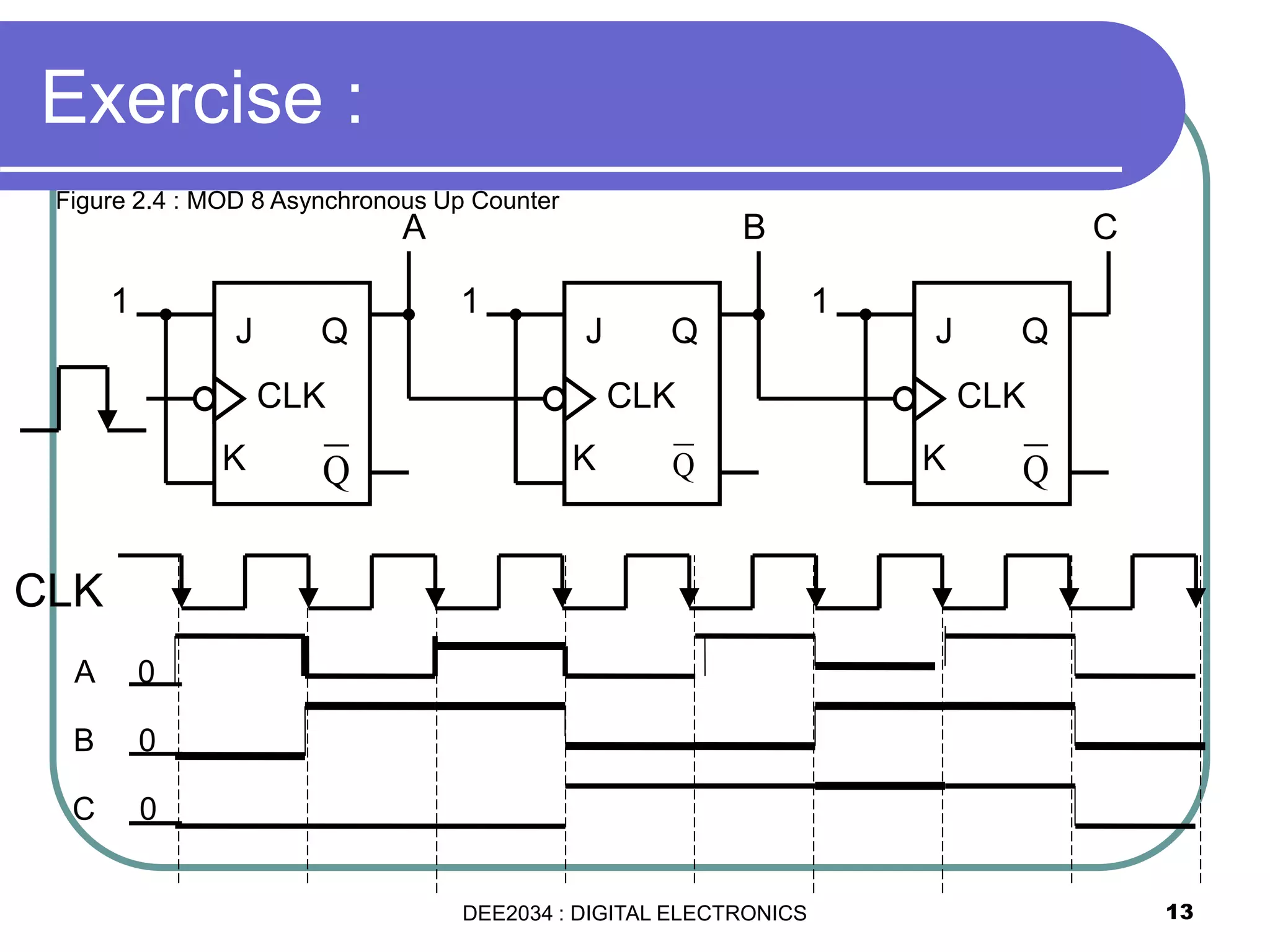
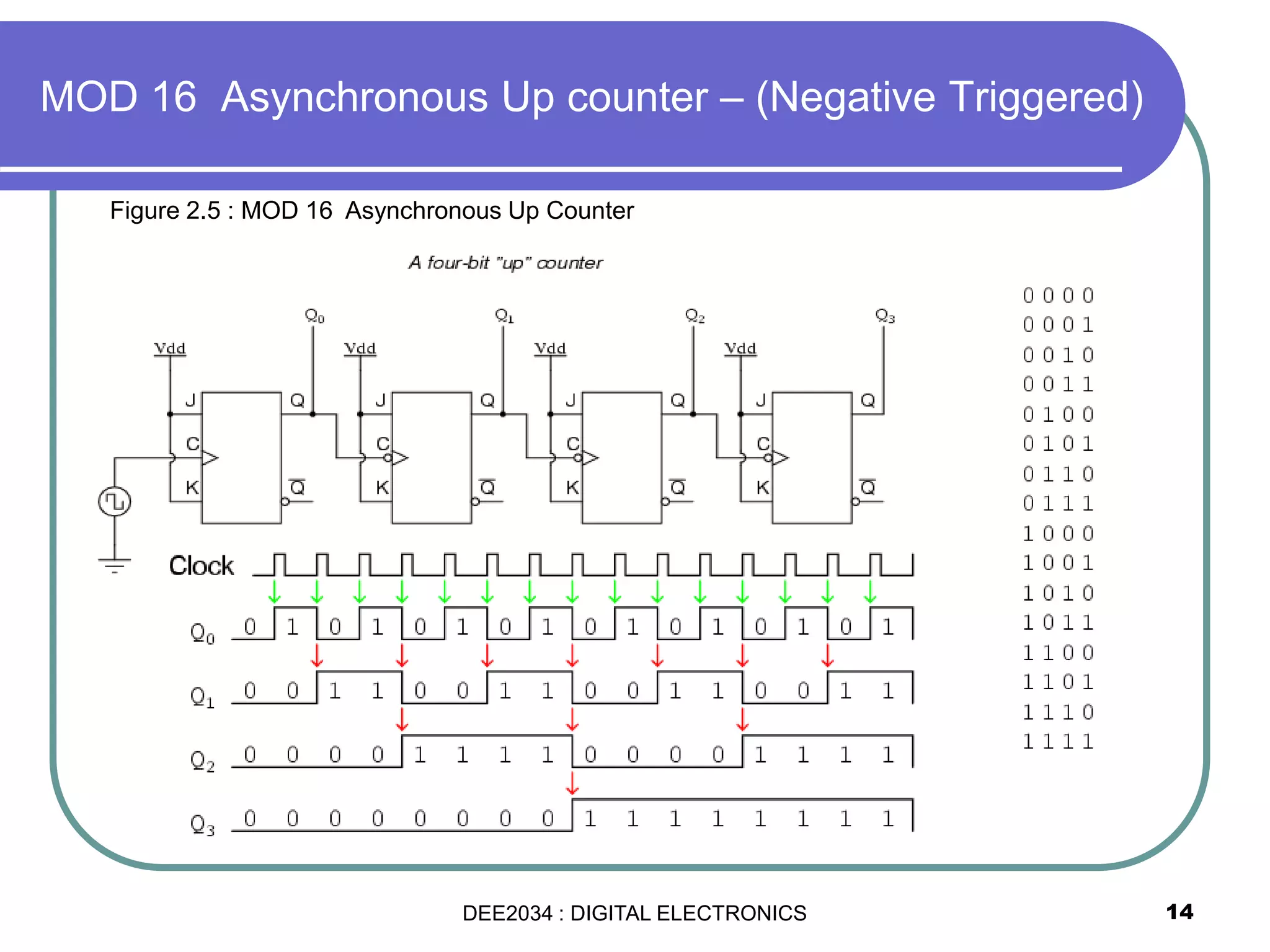
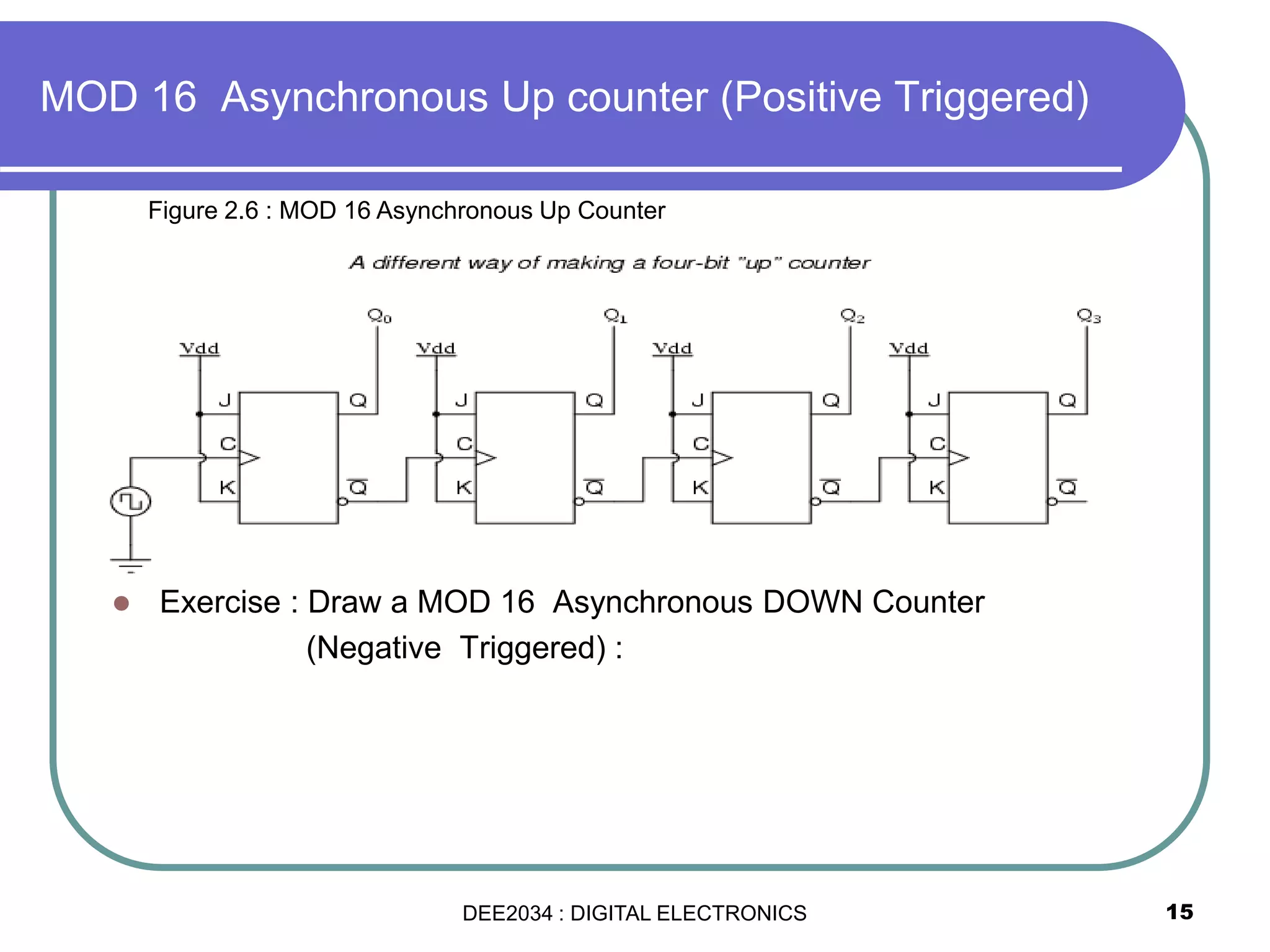
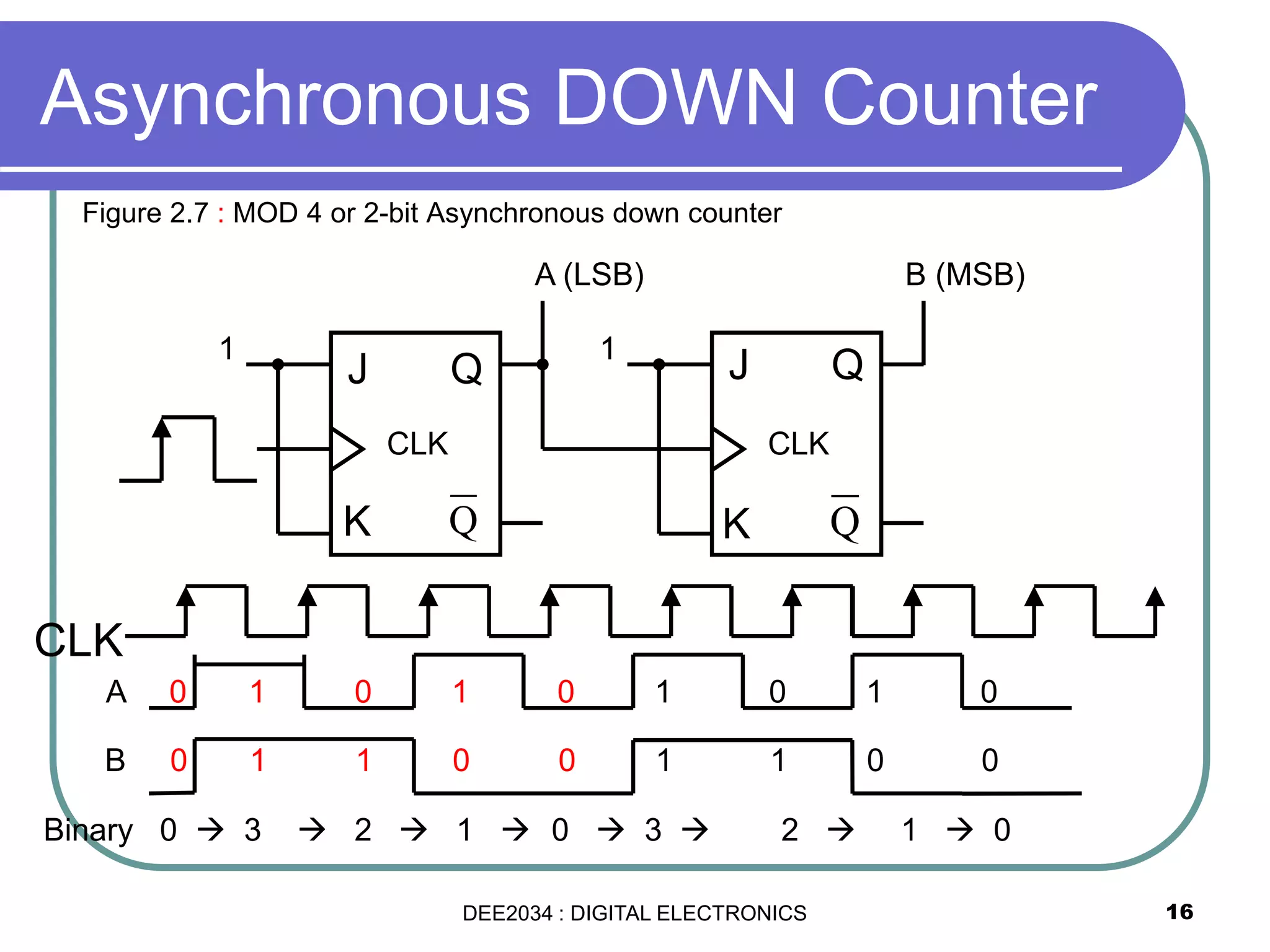
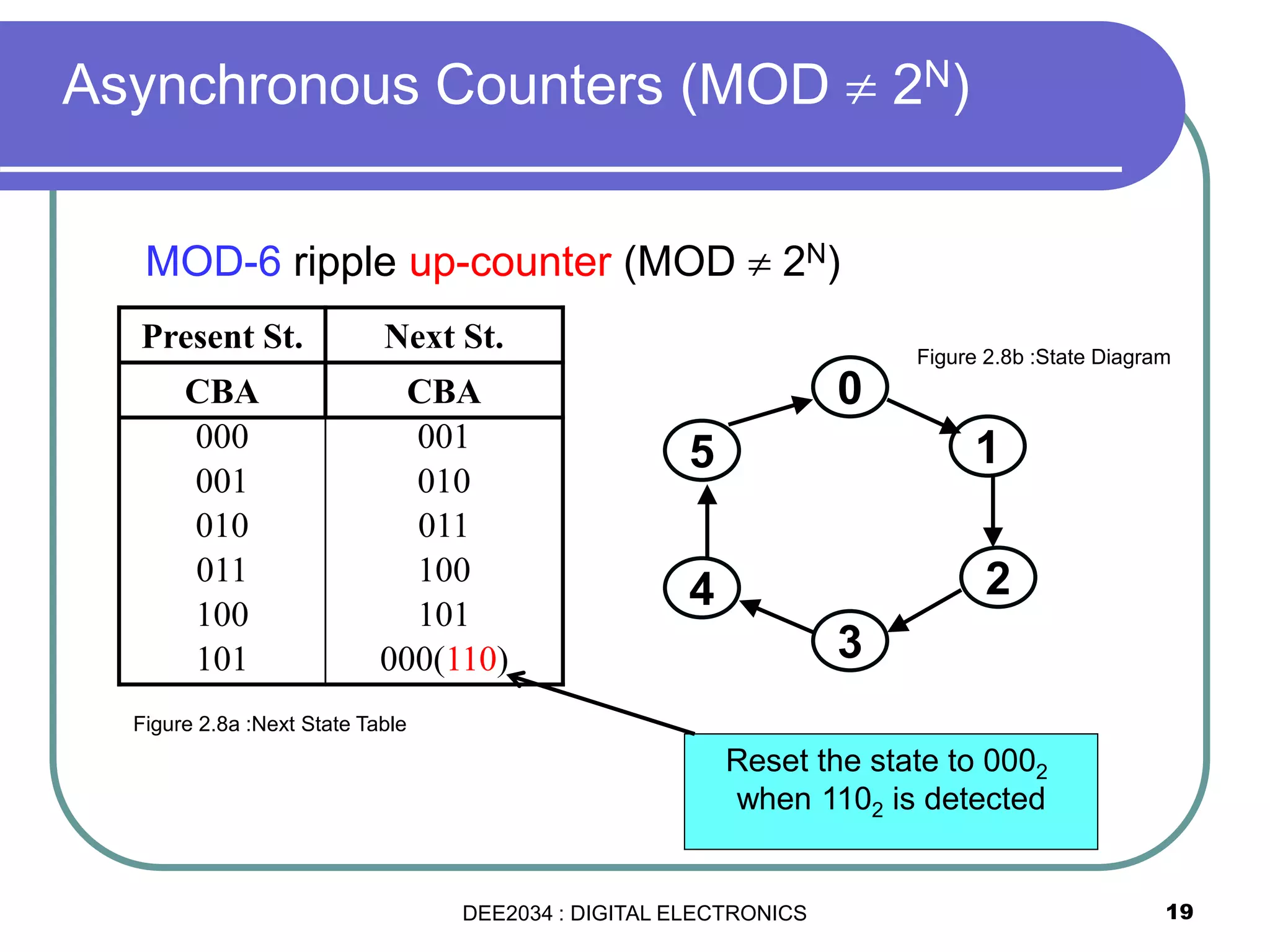
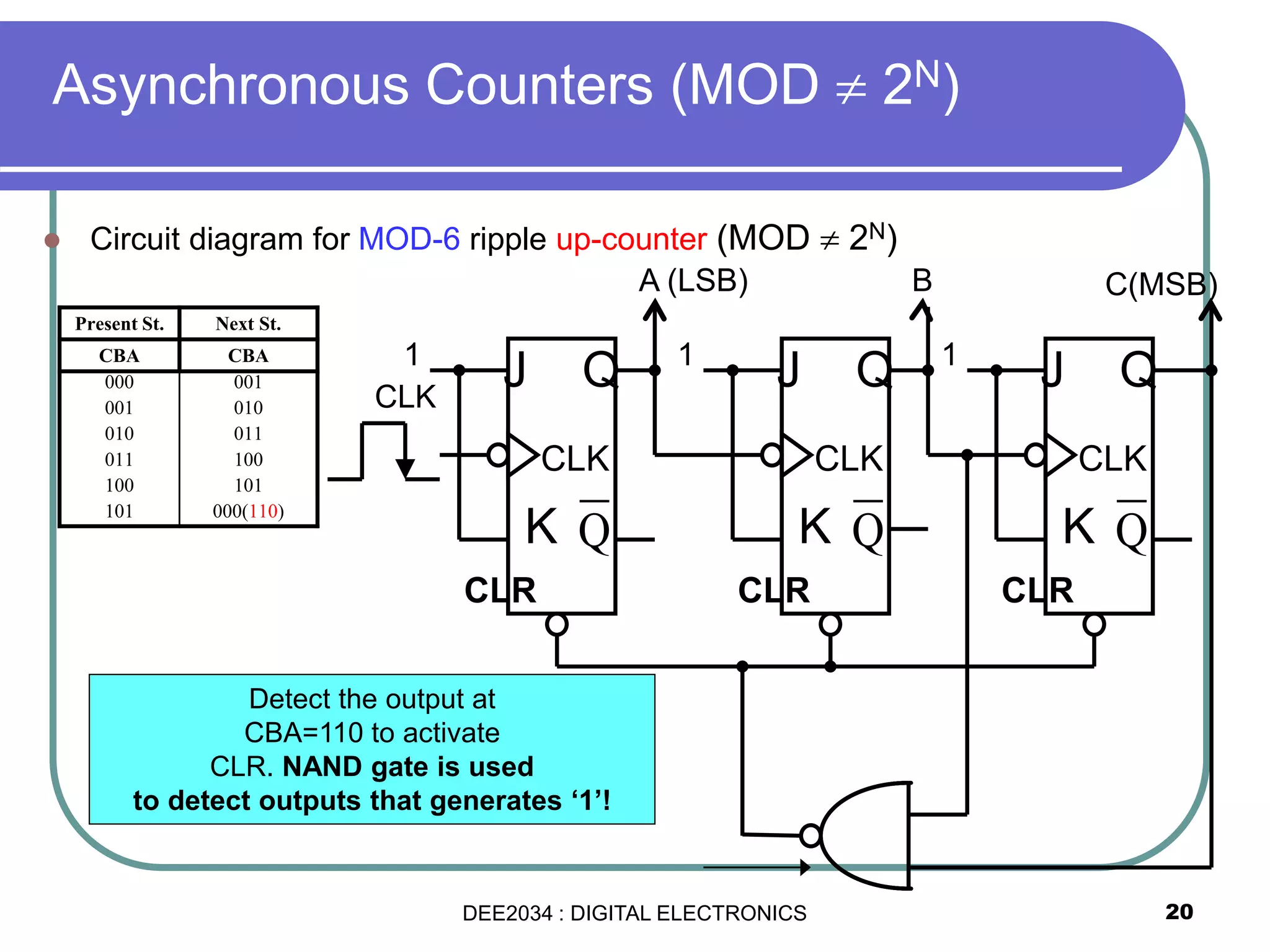
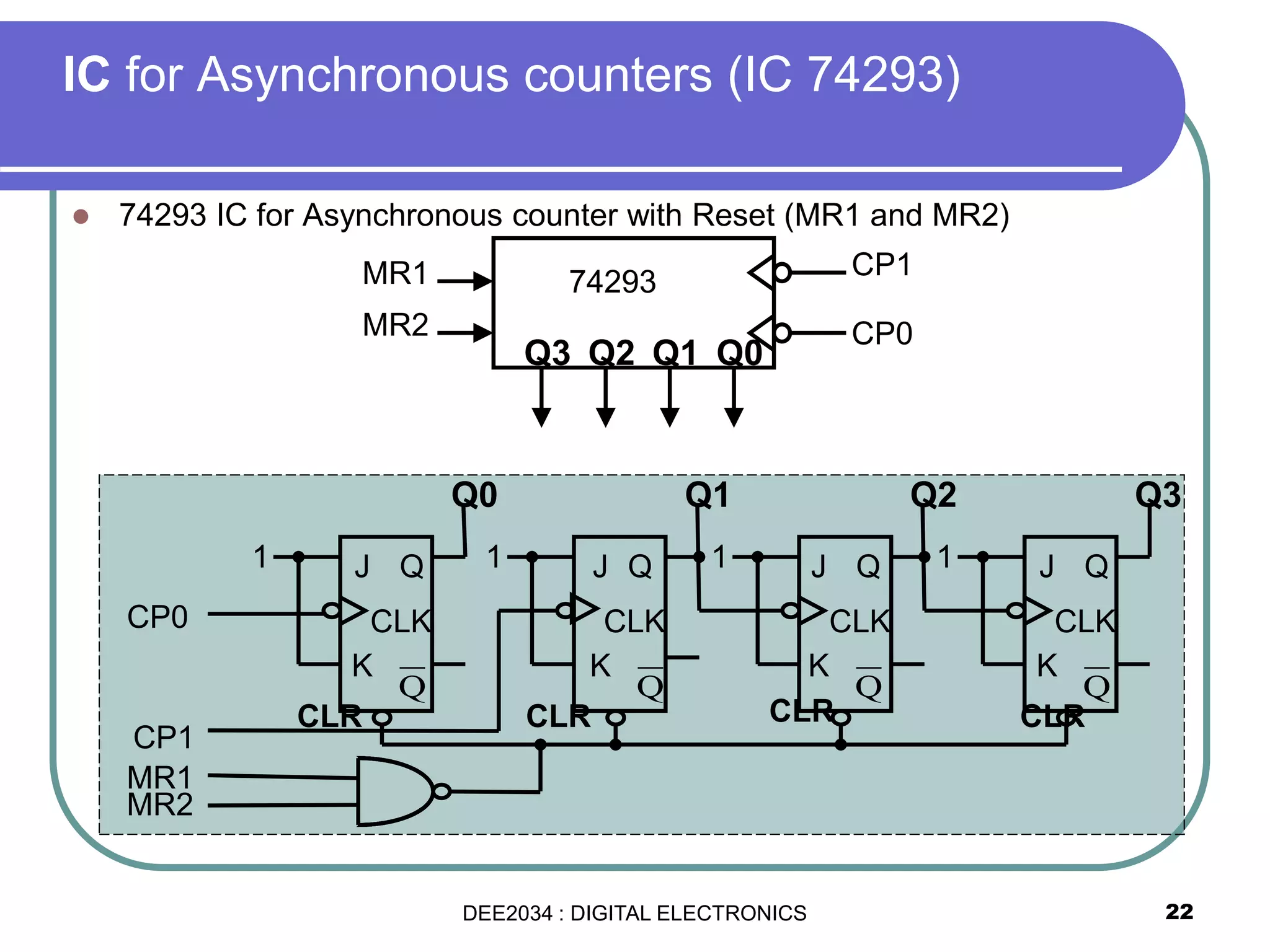
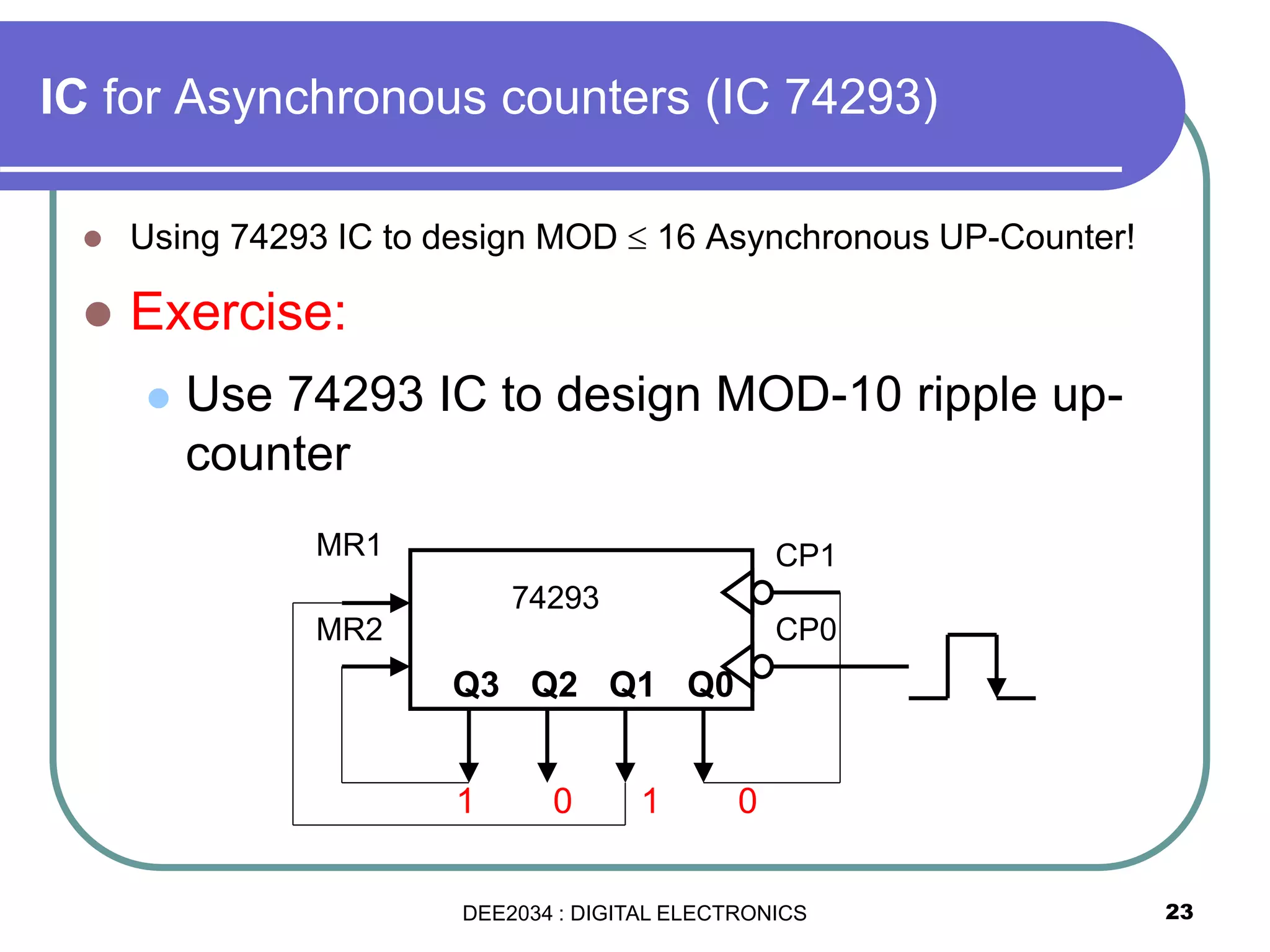
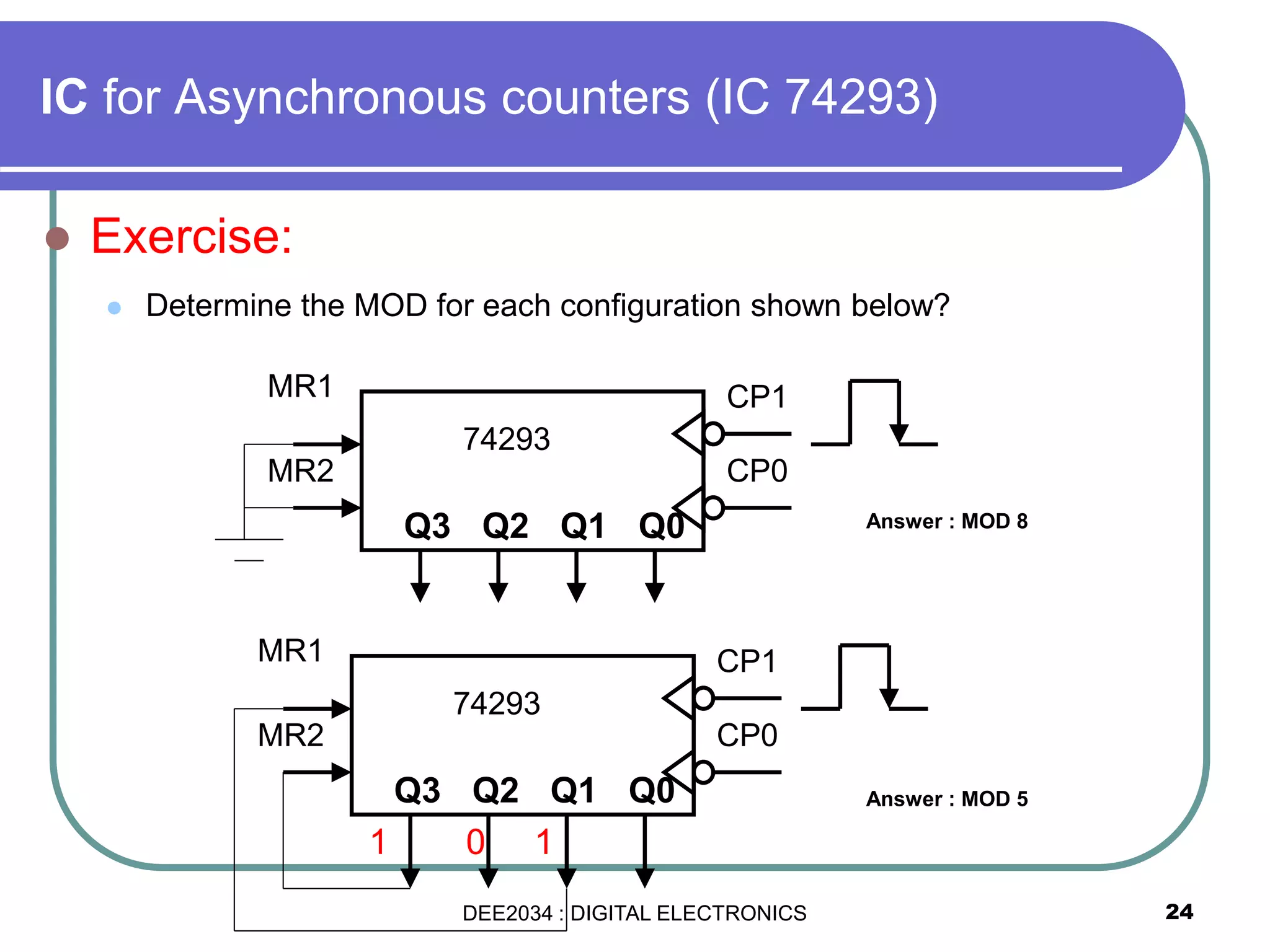
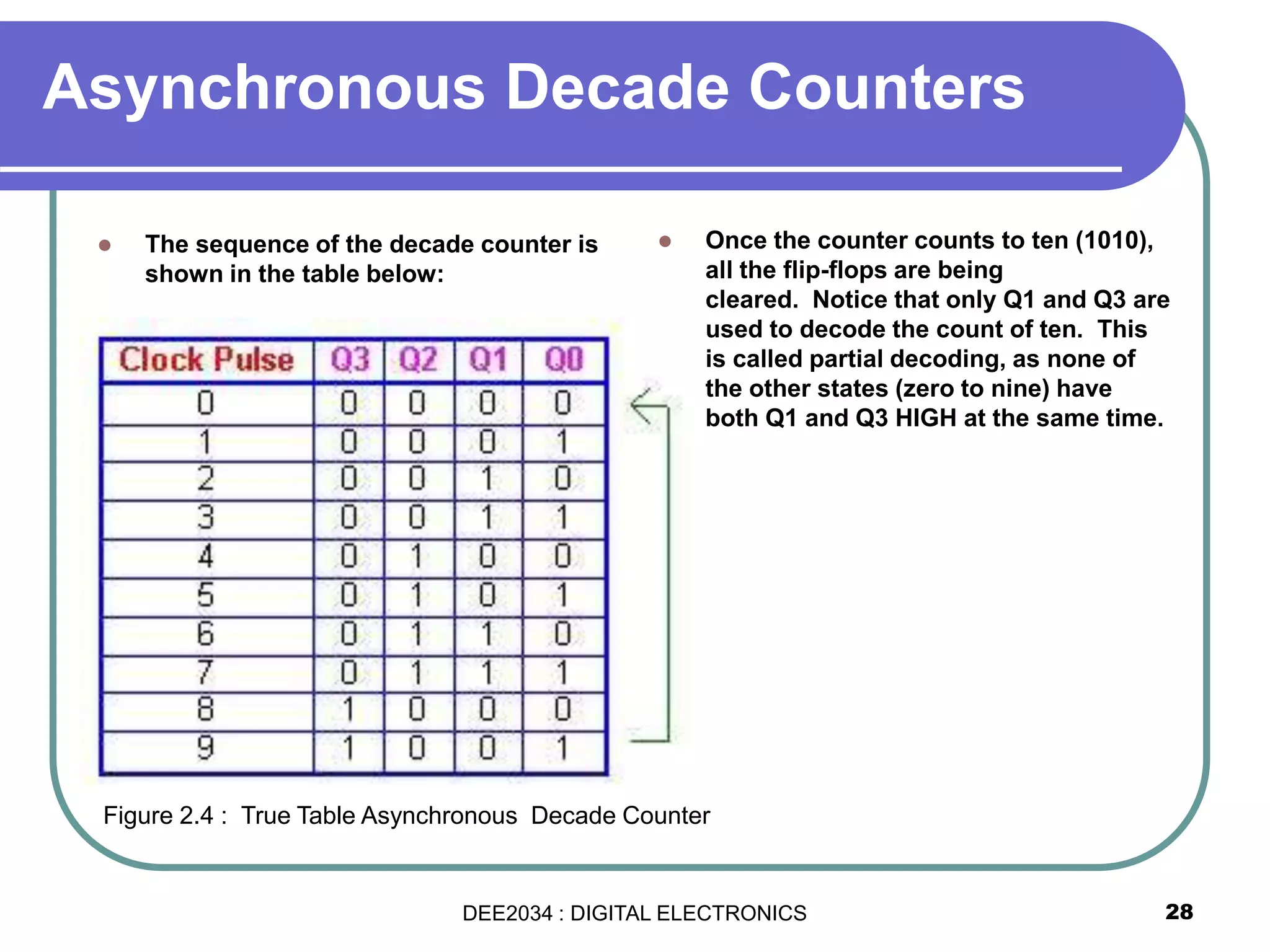
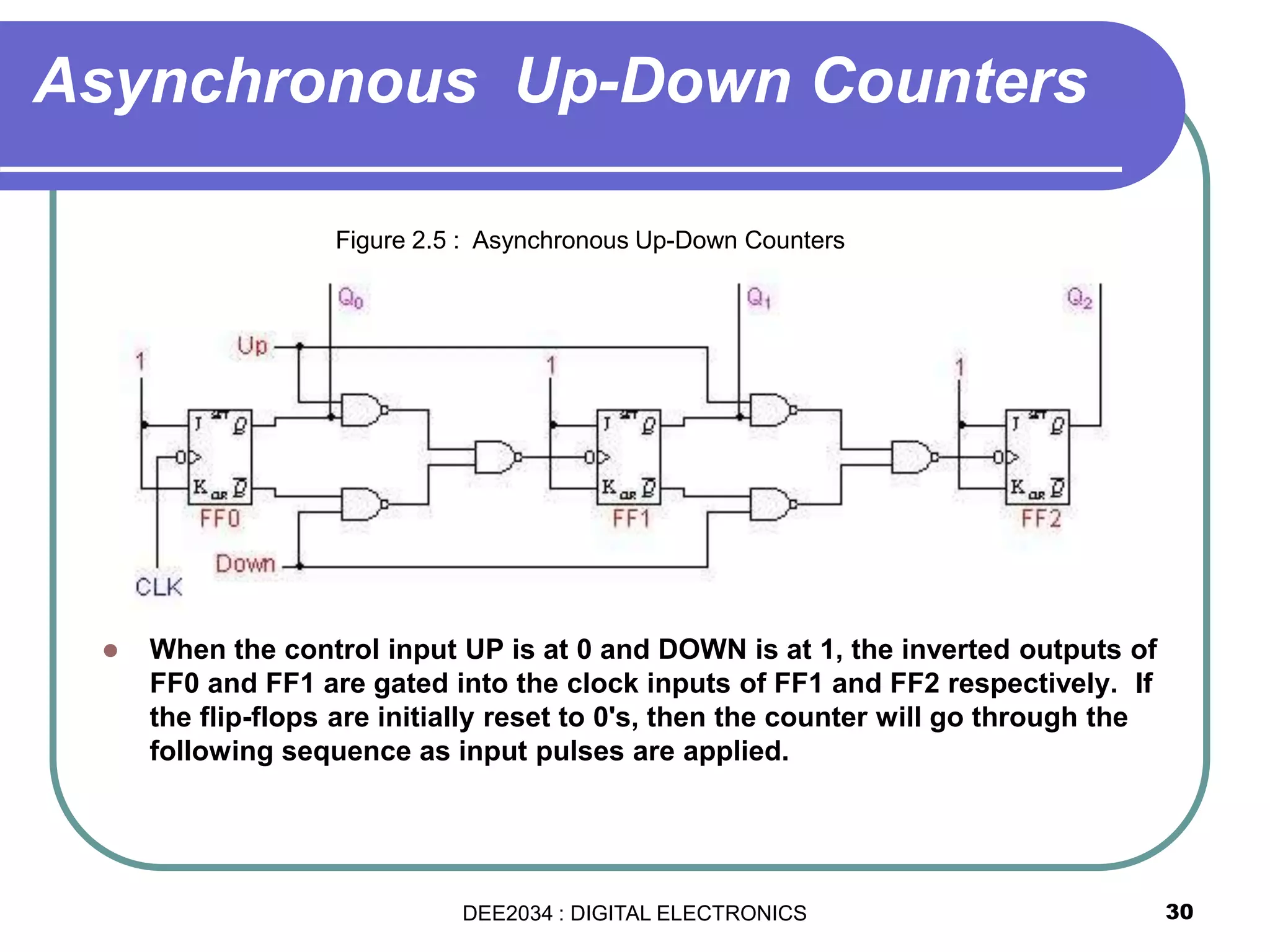
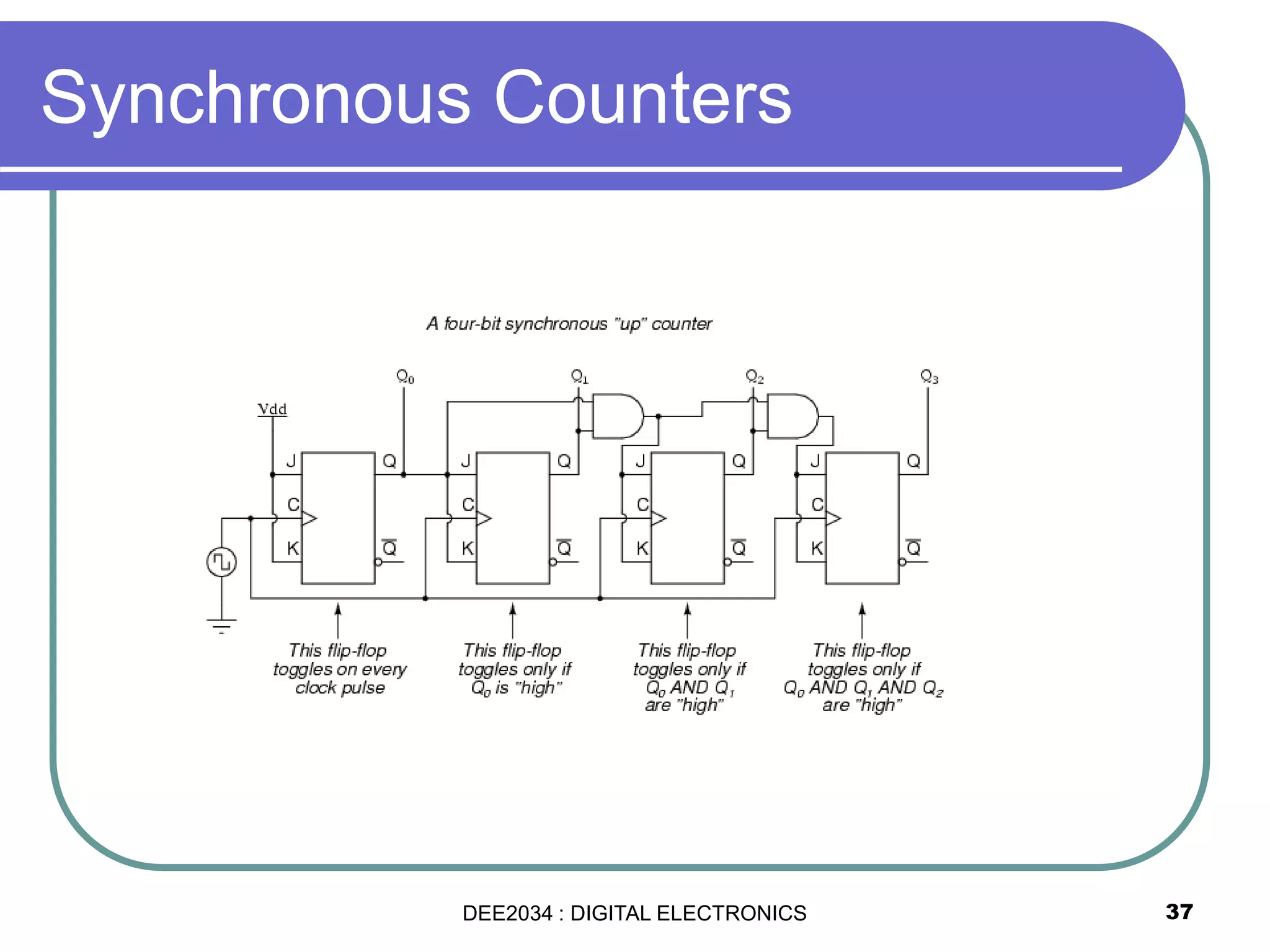
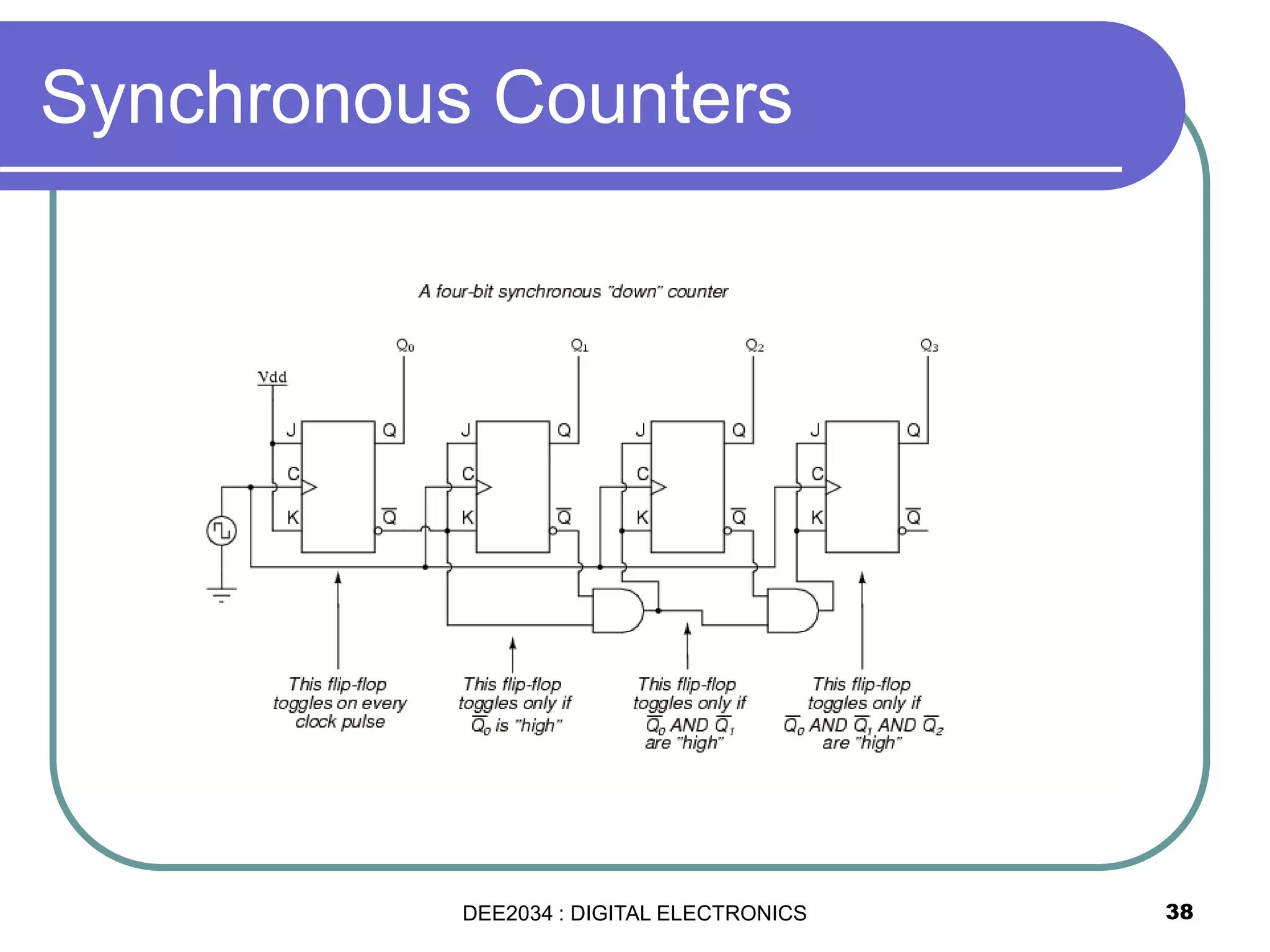
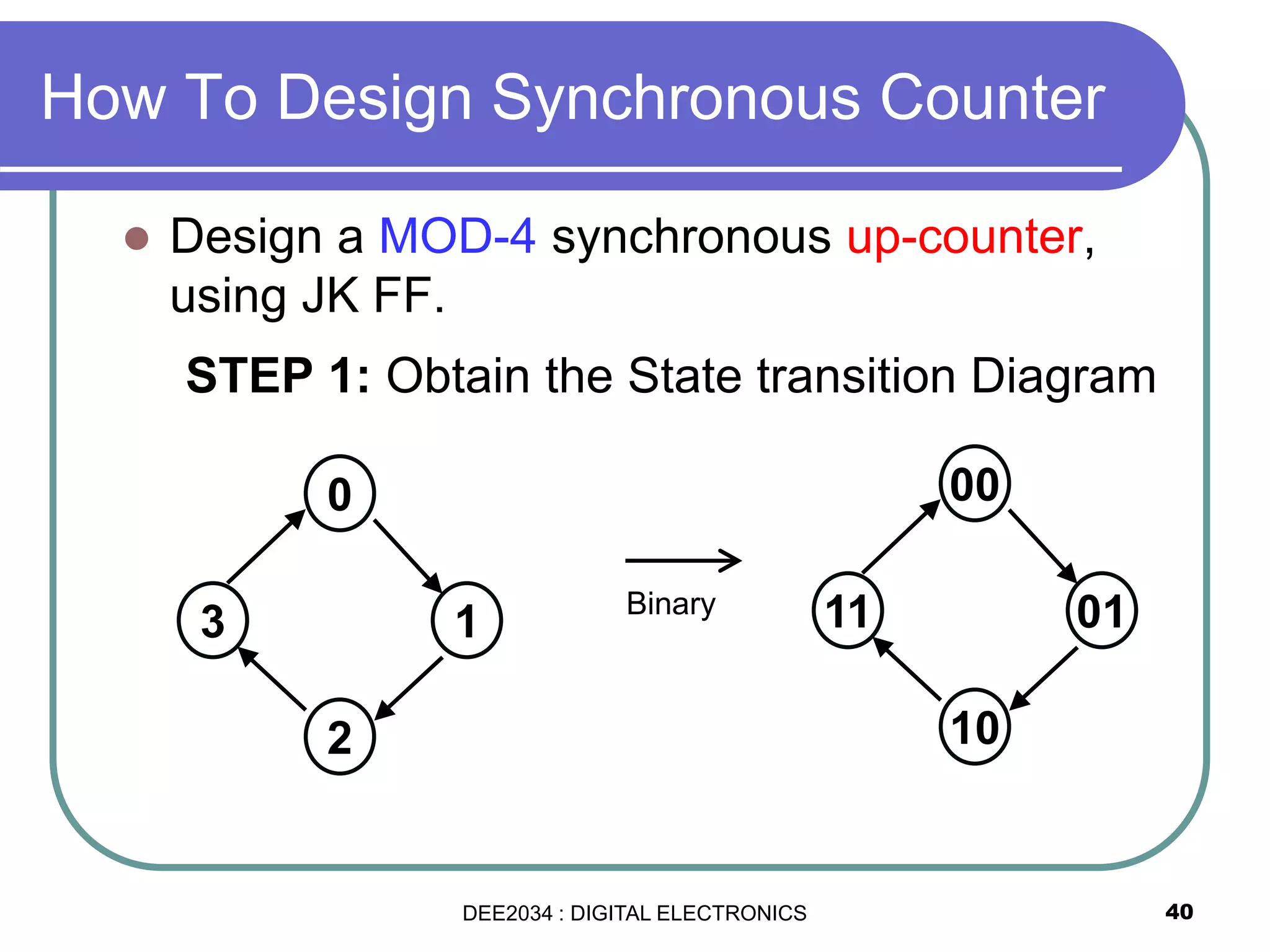
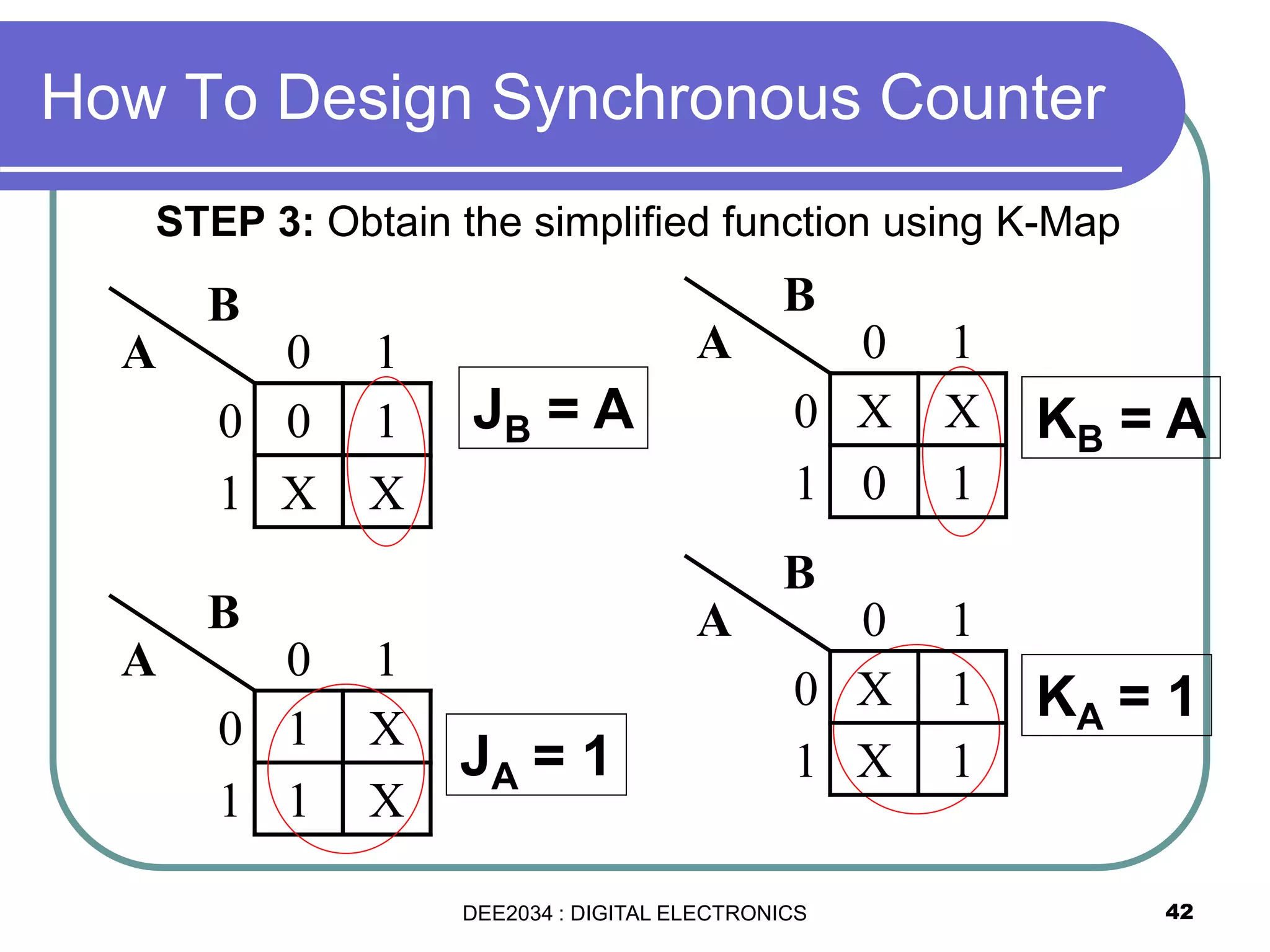
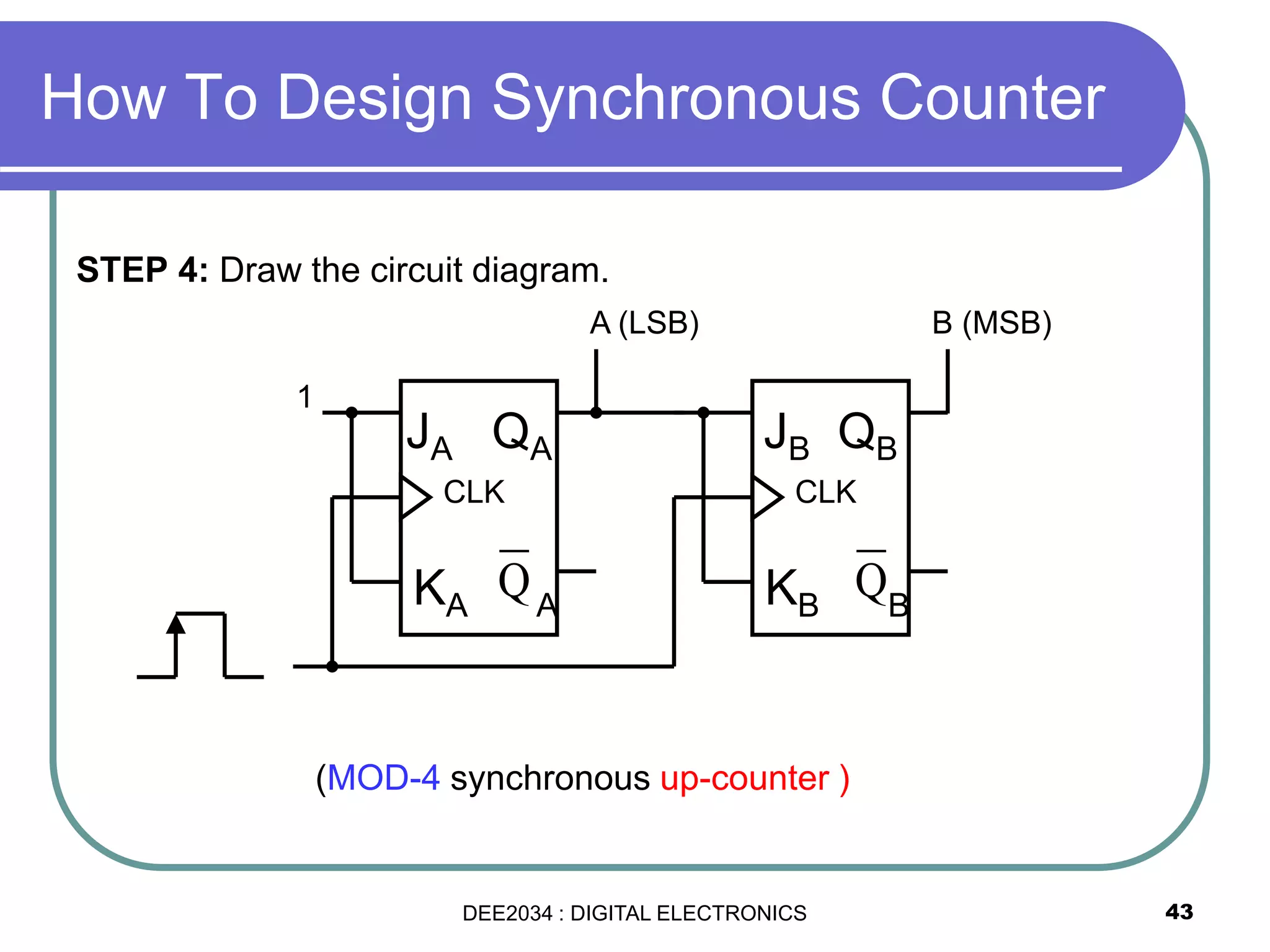
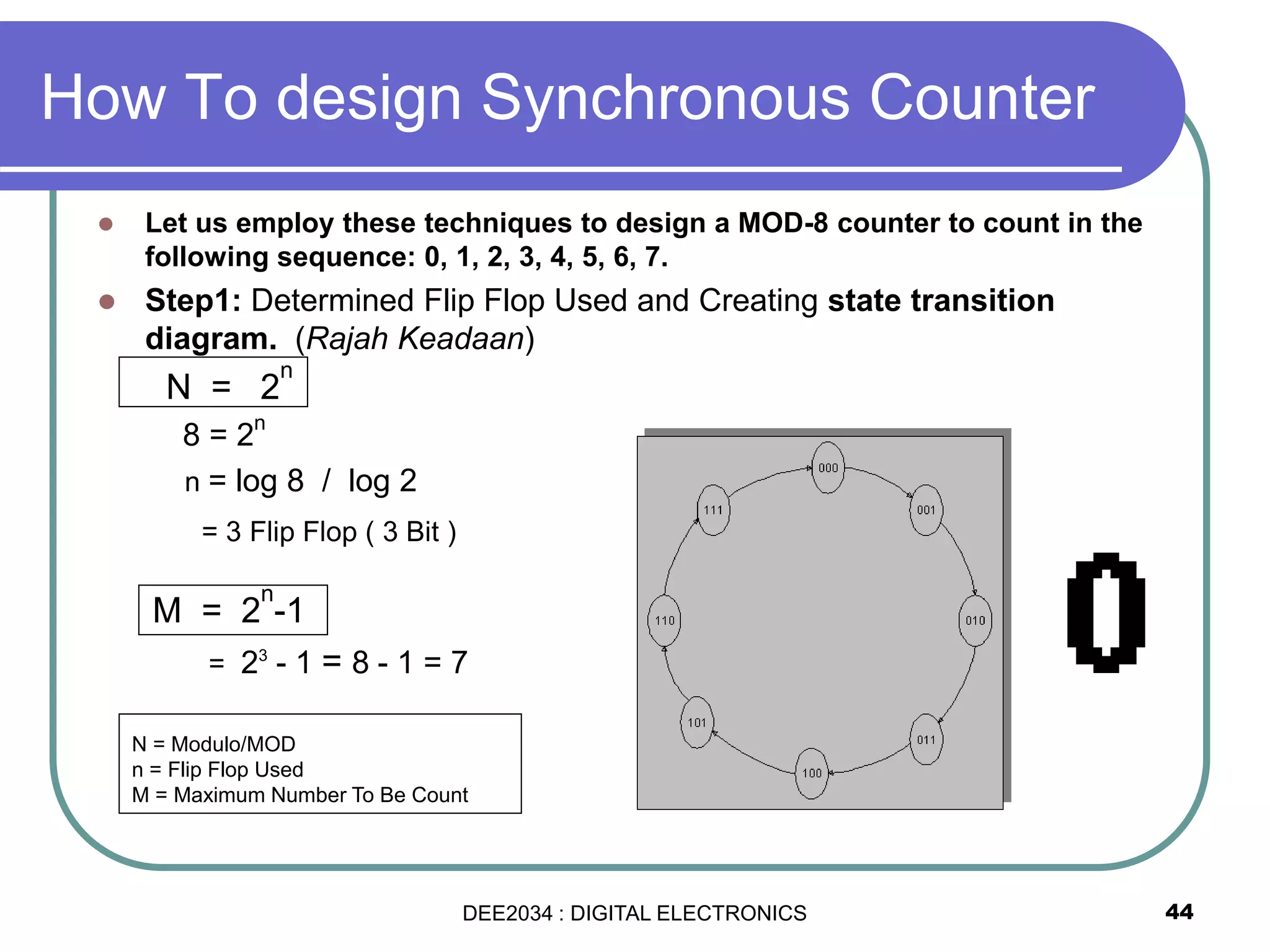
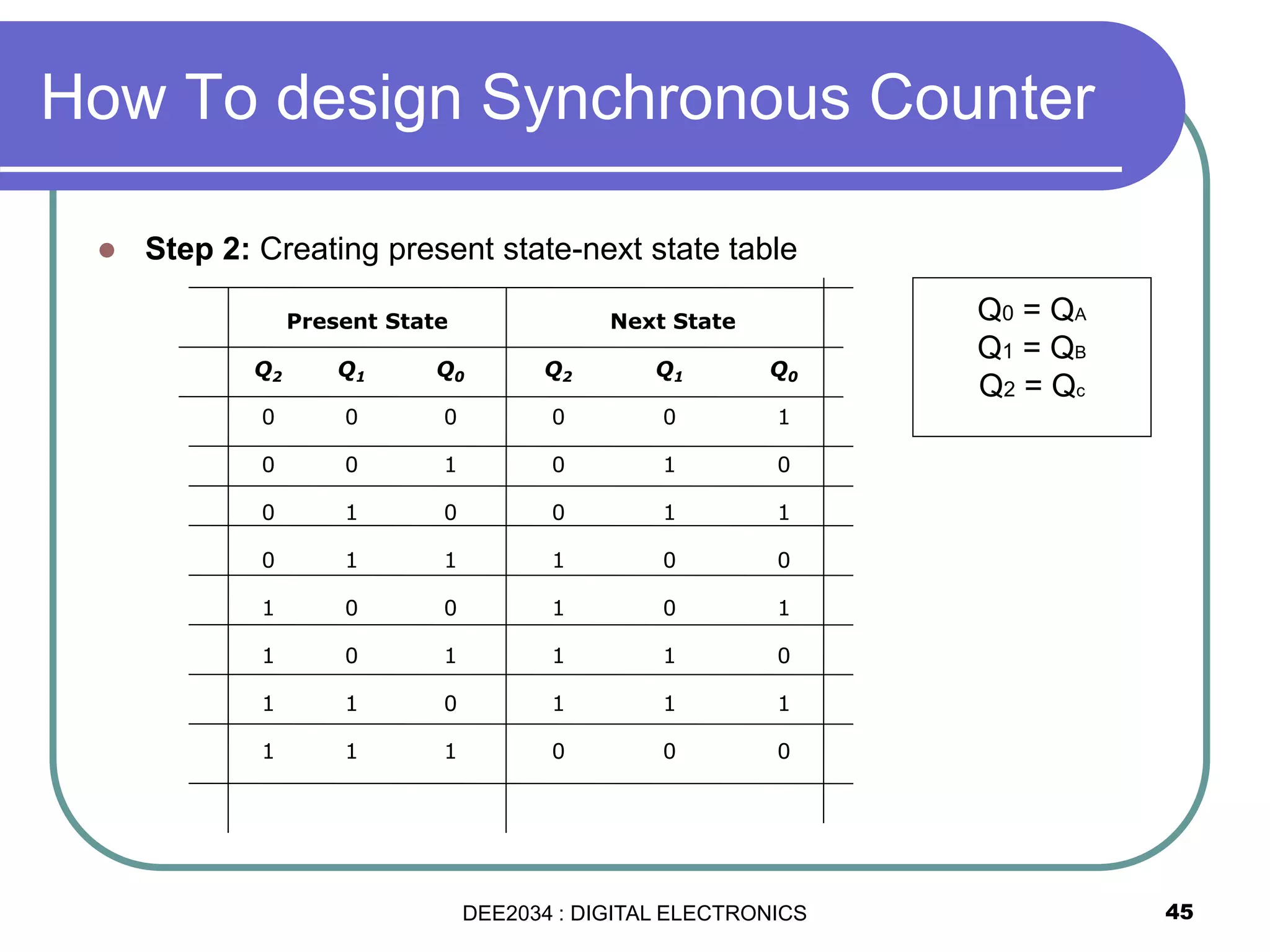
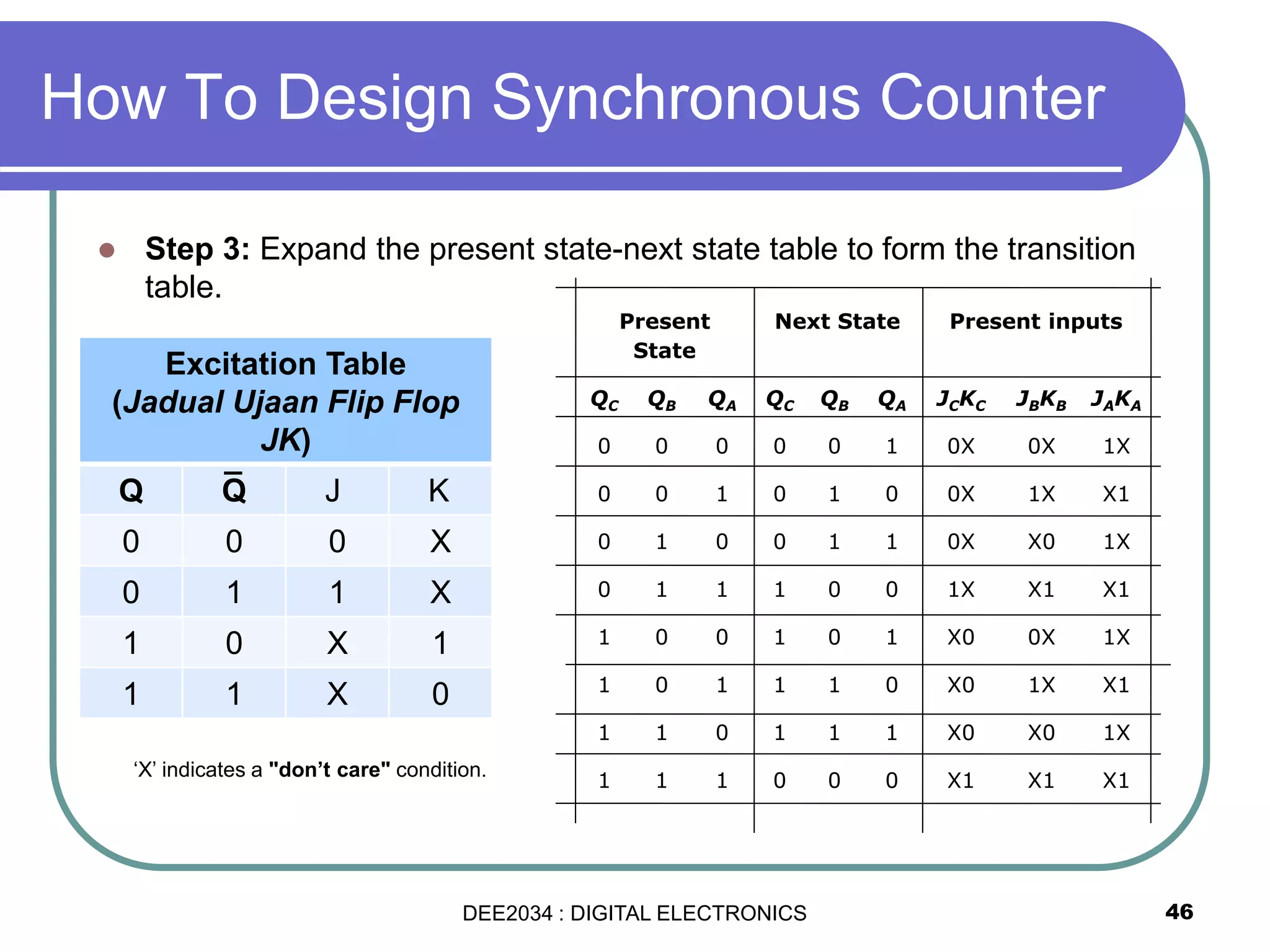
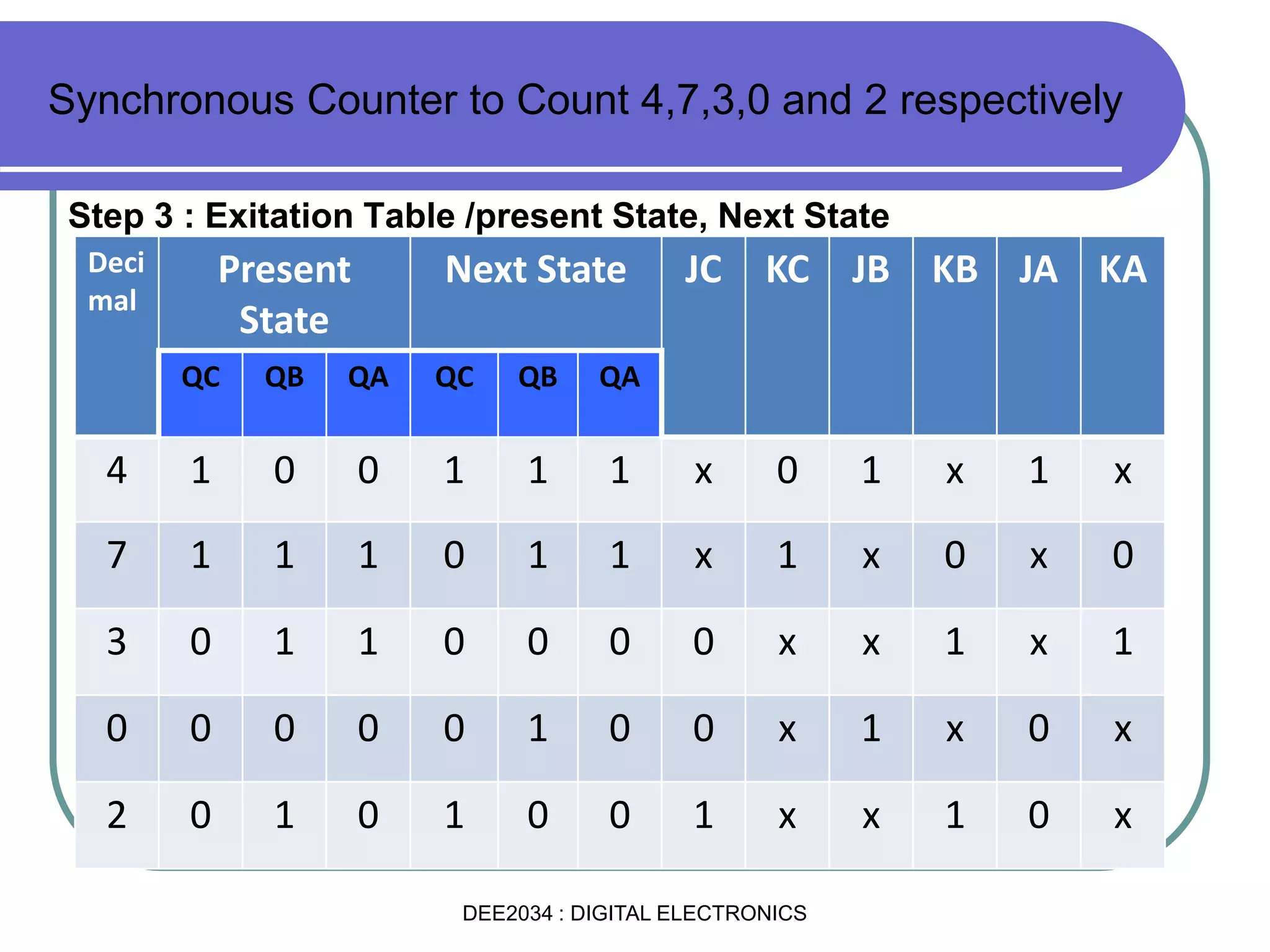
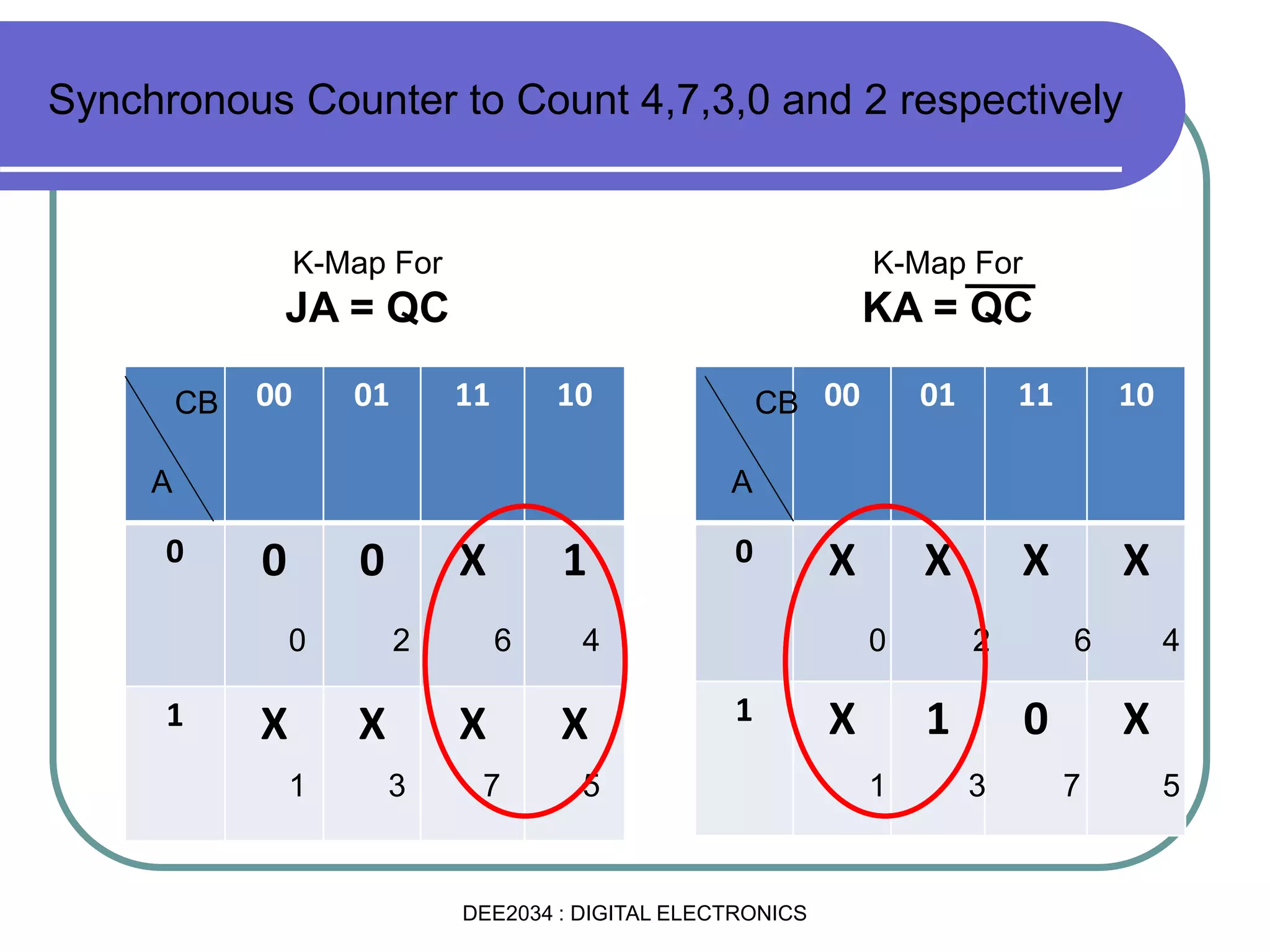
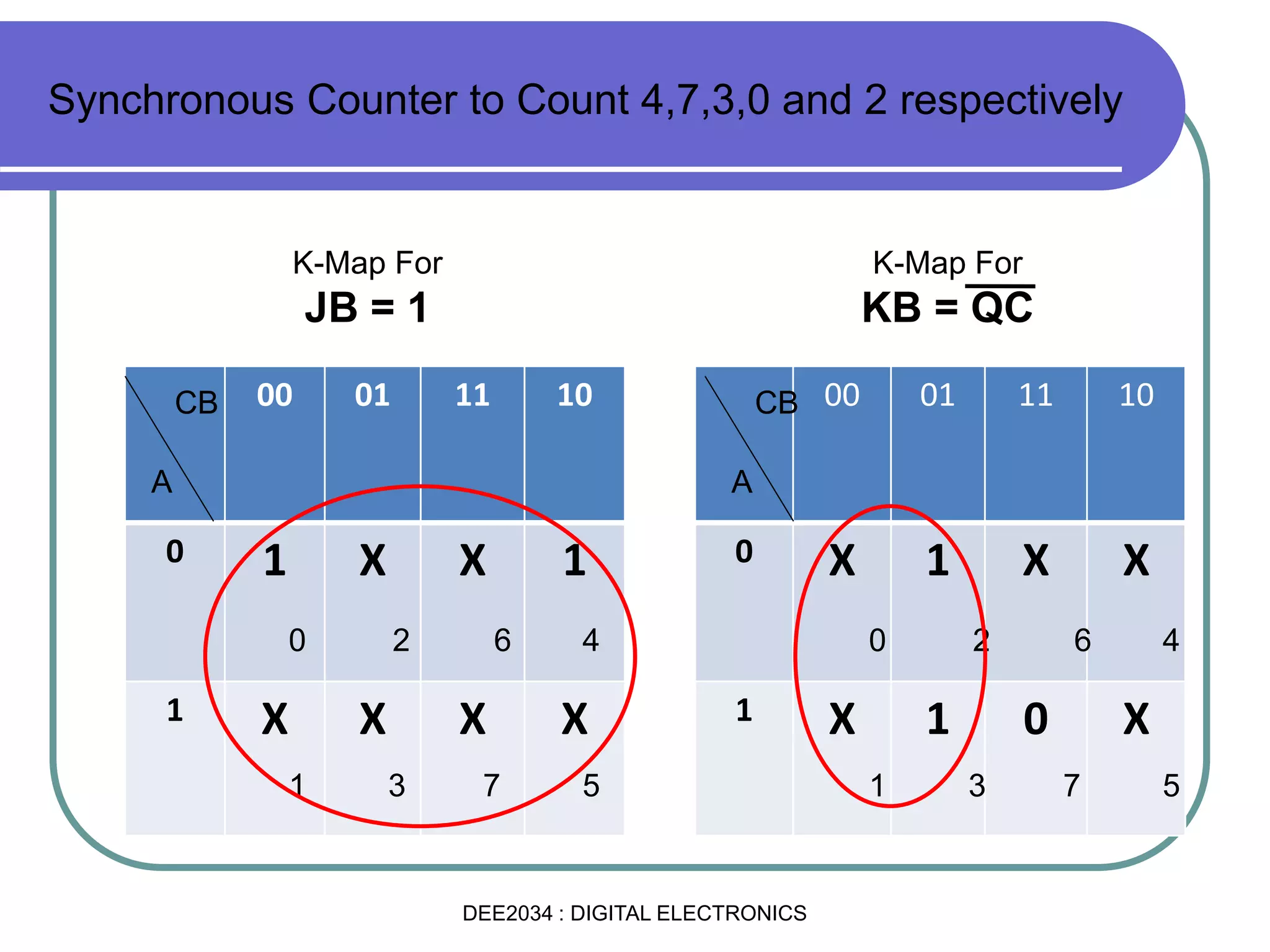
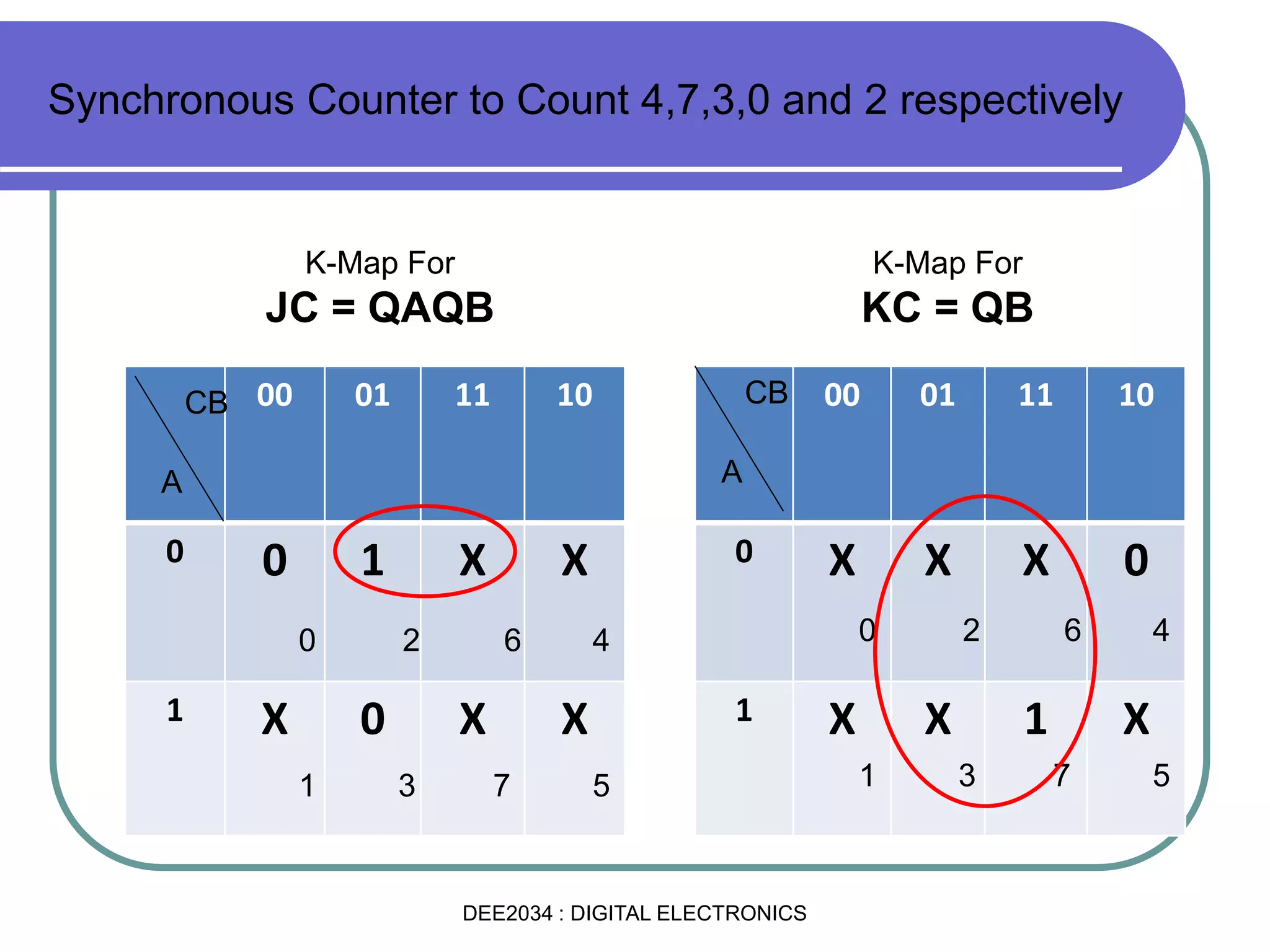
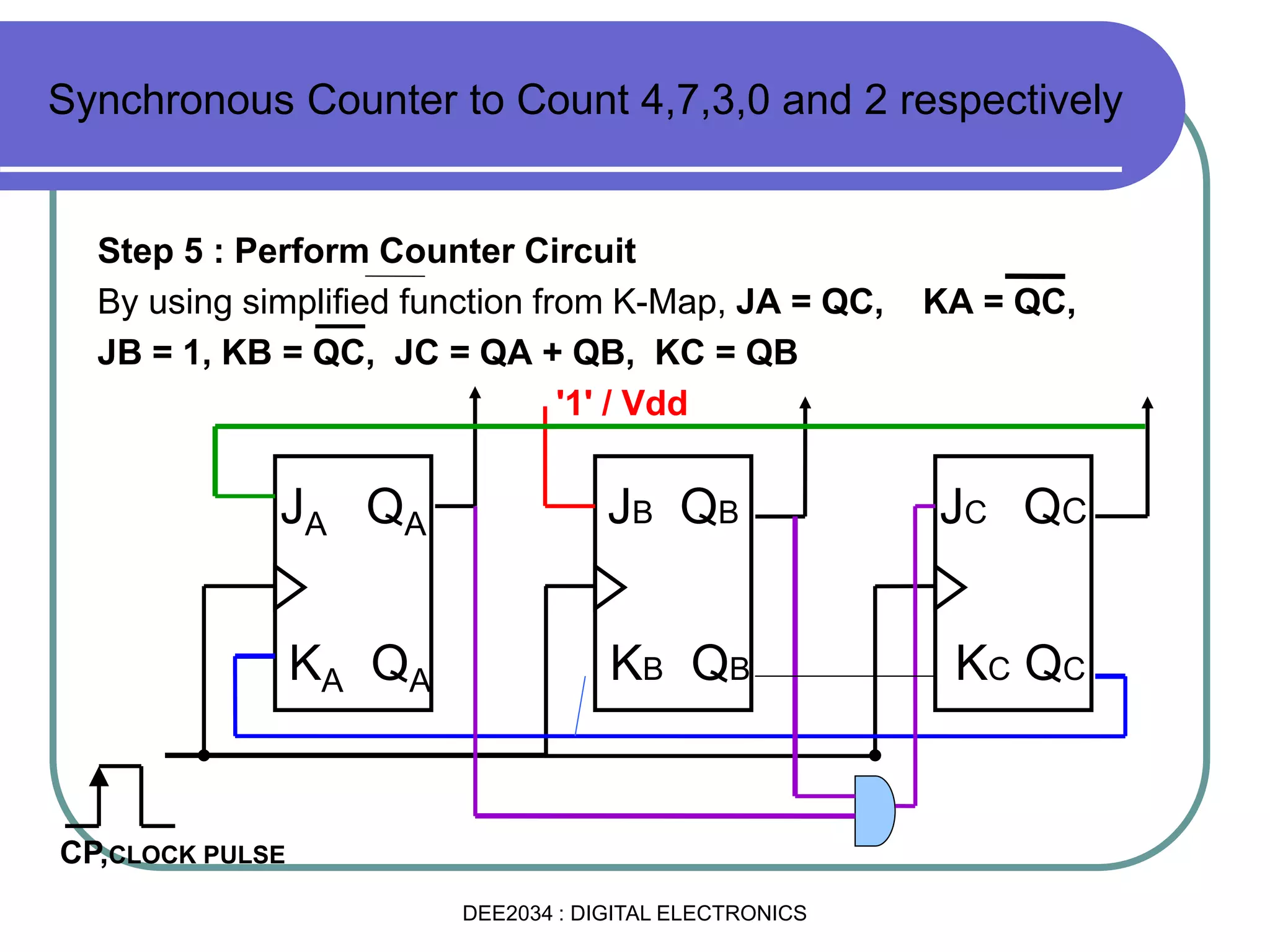
This document discusses asynchronous and synchronous counters. It begins by explaining the basic concepts of asynchronous and synchronous counters, and the differences between them. It then provides details on asynchronous up counters, down counters, and up/down counters. Examples are given of MOD-4, MOD-8, and higher MOD asynchronous counters. Synchronous counters are introduced which allow all flip-flops to change simultaneously on the clock pulse. Examples are provided of decade counters and using integrated circuits like the 74293 for building asynchronous counters.