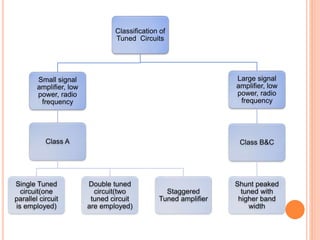
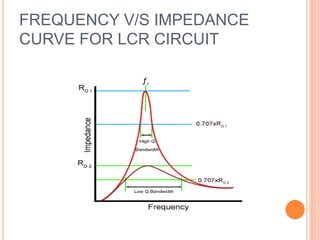
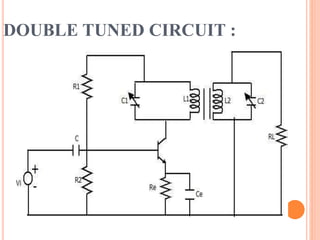
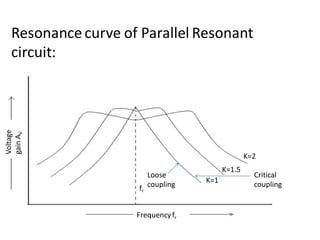
The document provides a comprehensive overview of tuned amplifiers, detailing their functionality, characteristics, and classifications including single, double, and stagger tuned amplifiers. It explains the principles of resonance in various circuit configurations, such as series and parallel resonant circuits, and discusses applications for low and large signal amplifiers. Additionally, it highlights the advantages and disadvantages of tuned amplifiers in communication systems and includes numerical examples to demonstrate calculations related to resonance frequency, quality factor, and bandwidth.

1. TUNED AMPLIFIER
Rakesh Mandiyahttps://in.linkedin.com/in/rakeshmandiya
rakesh.yadav1211@gmail.com

2. TUNED AMPLIFIER
 Introduction
 Band Pass Amplifiers
 Series & Parallel Resonant Circuits & their
Bandwidth
 Analysis of Single Tuned Amplifiers
 Analysis of Double Tuned Amplifiers
 Primary & Secondary Tuned Amplifiers with
BJT & FET
 Merits and de-merits of Tuned Amplifiers

3. DEFINITION:-
An amplifier circuit in which the load circuit is a tank
circuit such that it can be tuned to pass or amplify
selection of a desired frequency or a narrow band of
frequencies, is known as Tuned Circuit Amplifier.

4. CHARACTERISTICS OF TUNED AMPLIFIER
 Tuned amplifier selects and amplifies a single frequency
from a mixture of frequencies in any frequency range.
 A Tuned amplifier employs a tuned circuit.
 It uses the phenomena of resonance, the tank circuit which is
capable of selecting a particular or relative narrow band of
frequencies.
 The centre of this frequency band is the resonant frequency
of the tuned circuit .
 Both types consist of an inductance L and capacitance C
with two element connected in series and parallel.

5. RESONANCE CIRCUITS:
When at particular frequency the inductive reactance
became equal to capacitive reactance and the circuit then
behaves as purely resistive circuit. This phenomenon is
called the resonance and the corresponding frequency is
called the resonant frequency.
C
L
Tuned c ircuit

6. Resonance
circuits
Series Parallel

7. Classification of
Tuned Circuits
Small signal
amplifier, low
power, radio
frequency
Class A
Single Tuned
circuit(one
parallel circuit
is employed)
Double tuned
circuit(two
tuned circuit
are employed)
Staggered
Tuned amplifier
Large signal
amplifier, low
power, radio
frequency
Class B&C
Shunt peaked
tuned with
higher band
width

8. CLASSIFICATION OF TUNED AMPLIFIER
Tuned
amplifier
Small Signal
Amplifier
Single
Tuned
Amplifier
Double
Tuned
Amplifier
Stagger
Tuned
Amplifier
Large signal
Amplifier

9. CLASSIFICATION OF TUNED
AMPLIFIERS
Small Signal Tuned Amplifiers :- They are used to amplify
the RF signals of small magnitude.
They are further classified as:
(a) Single Tuned Amplifiers:- In this we use one
parallel tuned circuit in each stage.
(b) Double Tuned Amplifiers:- In this we use two
mutually coupled tuned circuits for every stage
both of tuned circuits are tuned at same freq.
(c) Stagger Tuned Amplifiers:- It is a multistage
amplifier which has one parallel tuned circuit for
every stage but tuned frequency for all stages are
slightly different from each other.

10. (2) Large signal tuned amplifiers:-
They are meant for amplifying large signals
in which large RF power is involved & distortion
level is also higher. But tuned circuit itself eliminates
most of the harmonic distortion.

11. BAND PASS AMPLIFIER:
 An amplifier designated to pass a definite band
of frequencies with uniform response.
 The new band pass amplifier perform both
function of low noise amplifier (LNA) & band
pass filter is proposed for application of 900Mhz
RF Front – end in wireless receivers .

12. BAND PASS AMPLIFIER:
It is having two differential stage comprising two
transistor.

13.  Main function of band pass filter to remove the
band noise ,which also contributes to the rejection
of image signals.
 Finally a band pass amplifier amplifies only a
band of frequency which lie in bandwidth of
amplifier & thus named as band pass amplifier .
BAND PASS AMPLIFIER

14. BAND PASS AMPLIFIER

15. BAND PASS FILTER

16. SERIES RESONANT CIRCUIT
It is the circuit in which all the resistive and
reactive components are in series.

17. SERIES RESONANT LC

18. SERIES RESONANT CIRCUIT
 Impedance Of The Circuit: -
Z = { R2 + (XL – Xc)2}1/2
Z = { R2 + (ωL – 1/ ωC)2}1/2
 For resonant frequency:-
(XL = XC )
XL = ωL = 2 π frL
XC = 1/ ωC = 1 / 2 π frC

19. SERIES RESONANT CIRCUIT
Since at resonance,
XL = Xc
2 π frL = 1 / 2ПfrC
fr = 1 / 2 π √LC
ωr = 1 / √LC

20. RESONANCE CURVE OF SERIES
RESONANT CIRCUIT :

21. QUALITY FACTOR
It is voltage magnification that circuit produces at
resonance is called the Q factor.
Voltage Magnification = Imax XL / Imin R
= XL/ R
At Resonance
XL/R = XC/R
ωrL / R = 1 / ωrRC

22. THUS
Qr = ωrL / R = 1/ ωrC R
= 2 π fr L / R
= (2 π L / R) * (1 / 2 π √LC )
= √(L/C) / R
= tanФ
{ tan Ф = power factor of coil }

23. IMPORTANT POINTS
(1) Net reactance , X = 0.
(2) Impedance Z = R .
(3) Power factor is unity.
(4) Power expended = 6 watt.
Current is so large & will produce large voltage
across inductance & capacitance will be equal in
magnitude but opposite in phase.
Series resonance is called an acceptor circuit
because such a circuit accepts current at one
particular frequency but rejects current at other
frequencies these circuit are used in Radio –
receivers .

24. REACTANCE CURVE SERIES
RESONANT CIRCUIT
XL = 2ΠfL
X = XL - XC XC = 1
2ΠfC
R
fr
current

25. PARALLEL OR CURRENT RESONANCE

26. PARALLEL OR CURRENT
RESONANCE
When an inductive reactance and a capacitance are
connected in parallel as shown in figure condition may
reach under which current resonance (also known as
parallel or anti- resonance ) will take palace. In practice,
some resistance R is always present with the inductor.
Such circuit is said to be in electrical resonance when
reactive(watt less) components of line current becomes
zero. The frequency at which this happened is known as
resonant frequency.
Current will be in resonance if reactive component of R-
L branch IR-L sinФ R-L = Reactive component of
capacitive branch, neglecting leakage reactance of
capacitor C

27. FREQUENCY V/S IMPEDANCE
CURVE FOR LCR CIRCUIT

28. CURRENT AT RESONANCE
Capacitive Current Ic = 2 π fr CV
Coil Current IR-L = V/Z
= V / √ R2+ (ωrL)2
ФR-L = Cos-1(R/Z)
ФR-L = Sin-1(2ПfrL/Z)

29. ( V / √ R2+ (ωrL)2 ) * (ωrL / √ R2+ (ωrL)2 ) = ωrCV
C = L / (R2+ (ωrL)2
ωr = (1 / √LC) * (( 1- CR2/L) )1/2
ωr = √(1/LC – R2/L2)
fr = ωr /2 π
= (1/2 π ) * ((1/LC)- (R2 / L2))

30. RESONANCE CURVE OF PARALLEL
RESONANT CIRCUIT :
With low resistance
With high resistance
current
Resonant
frequency
fR

31. Active component of coil
IA = IR- L cosФR-L
= (V/Z) * (R/Z)
= VR/Z2
Reactive component of coil
IR = IR-L sinФ
= (V/Z ) * (2 π frL/Z )

32. Since at resonance
Reactive component of coil current = Capacitive current
(V / Z ) * (2 π frL / Z) = 2 π frCV
Z = √(L/C) ………..(1)
Line current IL = Active component of coil current
= IA
= IR-L cosФR-L
= VR/Z2 [using (1)]
= VR(C/L)
IL = [ V / (L/RC) ]
(L/RC) = Effective or equivalent dynamic impedance of
parallel circuit at resonance.

33. IMPORTANT POINTS FOR CURRENT OR
PARALLEL RESONANCE:
(1) Net susceptance is zero
(1 / XC ) = ( XL / Z2 )
(2) Admittance = Conductance
(3) Power factor is unity as reactive ( wattles)
components of the current is zero
(4) Impedance is purely resistive
ZMax = (L / CR)
(5) ILine(Min) = V / ( L/CR ) ( in phase with applied
voltage)

34. (6) f = (1/2П) * ( √(1/LC) – (R2/ L2)) Hz
The frequency at which the net susceptance curve
crosses the frequency axis is called the resonant
frequency .
At this point impedance is maximum or admittance
is minimum & is equal to G , consequently (I) Line is
minimum .

35.  Band with of parallel resonant circuit
B.W. = (f2 – f1)
 Quality Factor
Q = XL / R
= 2ПfrL / R
Quality factor determines sharpness of resonance
curve and selectivity of circuit.
Higher the value of quality factor more selective the
tuned circuit is.

36. CHARACTERSTICS OF PARALLEL
OR CURRENT RESONANCE
 Admittance is equal to conductance.
 Reactive or watt less component of line current is zero
hence circuit power factor is unity.
 Impedance is purely resistive , maximum in
magnitude and is equal to L/CR.
 Line current is minimum and is equal to
V / (L/CR)
in magnitude and is in phase with the applied voltage.

37. REACTANCE CURVE PARALLEL
RESONANT CIRCUIT
XL = 2ΠfL
X = XL - XC
current
1
XC =
2ΠfC
R

38. (1) SINGLE TUNED AMPLIFIER
+
Vs
Cin R1
R2
CeRe
Cc RL
LC
Vcc

39. (1) SINGLE TUNED AMPLIFIER
• O/P of this amplifier may be taken either with the
help of Capacitive.
• A parallel tuned circuits is connected in the collector
circuit.
Tuned voltage amplifier are usually employed in RF
stage of wireless communication , where such
circuits are assigned the work of selecting the
desired carrier frequency and of amplifying the
permitted pass-band around the selected carrier
frequency.

40. SINGLE TUNED AMPLIFIER
 Tuned amplifier are required to be
R1, R2, & Re = For biasing & stabilization circuit.
Ce = By pass capacitor
L-C = Tuned circuit connected in collector,
the impedance of which depend
upon frequency, act as a collector
load.
If i/p signal has same frequency as resonant frequency
of L-C circuit . Large amplification will be obtain
because of high impedance of L-C ckt.

41. SINGLE TUNED AMPLIFIER
USING FET

42. SINGLE TUNED AMPLIFIER USING FET
 In the shown figure the single tuned amplifier is
depicted using a field effect transistor.
 The value of L and C is selected as per the desired
frequency level.
 One of the components either L or C is variable so
as to adjust the variable frequency.

43. THE HIGH FREQUENCY SIGNAL TO BE APPLIED BETWEEN BASE
& EMITTER. THE RESONANT FREQUENCY OF CIRCUIT IS MADE
EQUAL TO FREQUENCY OF I/P SIGNAL BY VARYING L OR C .
NOW TUNED CKT WILL OFFER VERY HIGH IMPEDANCE TO
THE SIGNAL FREQ. & THUS LARGE O/P APPEAR ACROSS IT.
AV = ( Β RAC )/ RIN
{ RAC = TUNED CIRCUIT IMPEDANCE}
= Β(L/CR)/ RIN
AV = ΒL / ( CRRIN )
BANDWIDTH = (F2- F1 )
THE AMPLIFIER WILL AMPLIFY ANY FREQ. WELL WITHIN THIS
RANGE.
CIRCUIT OPERATION

44. LIMITATION
 This tuned amplifier are required to be highly selective.
But high selectivity required a tuned circuit with a high Q-
factor .
 A high Q- factor circuit will give a high Av but at the
same time , it will give much reduced band with because
bandwidth is inversely proportional to the Q- factor .
 It means that tuned amplifier with reduce bandwidth
may not be able to amplify equally the complete band of
signals & result is poor reproduction . This is called
potential instability in tuned amplifier.

45. DOUBLE TUNED CIRCUIT :

46. DOUBLE TUNED CIRCUIT
 The problem of potential instability with a single tuned
amplifiers overcome in a double tuned amplifier which
consists of independently coupled two tuned circuit :
(1) L 1C1 in collector circuit
(2) L2 C2 in output circuit
A change in the coupling of two tuned circuit
results in change in the shape of frequency response .
By proper adjustment of coupling between two coils of
two tuned circuits, the required results are :
 High selectivity
 High voltage gain
 Required bandwidth

47. CIRCUIT OPERATION
 The resonant freq. of tuned circuit connected in collector circuit is
made equal to signal freq. by varying the value of C1.
 Tuned circuit (L 1C1) Offer very high impedance to
signal frequency & this large o/p is developed across it.
 The o/p of (L1C1) is transferred to (L2C2) through
mutual inductance.
 Thus the freq. response of double tuned circuit depends upon
magnetic coupling of L1 & L2.
 Most suitable curve is when optimum coefficient of coupling
exists between two tuned circuit .The circuit is then highly selective
& also provides sufficient amount of gain for a particular band of
frequency.

48. Voltage
gainAV
Frequencyfr
K=2
K=1.5
K=1
fr
Critical
coupling
Loose
coupling
Resonance curve of Parallel Resonant
circuit:

49. SHUNT PEAKED CIRCUITS FOR INCREASED
BANDWIDTH
For expanding bandwidth we use various combinations of BJT &
FET(MOS) in series or shunt so that we can use Stagger tuned
amplifiers.
Shunt Peaking
If a coil is placed in parallel (shunt) with the output signal path,
the technique is called SHUNT PEAKING. R1 is the input-
signal-developing resistor. R2 is used for bias and temperature
stability. C1 is the bypass capacitor for R2. R3 is the load
resistor for Q1 and develops the output signal. C2 is the
coupling capacitor which couples the output signal to the next
stage.

50. SHUNT PEAKED CIRCUITS FOR
INCREASED BANDWIDTH :

51. STAGGER TUNED AMPLIFIERS
 It is a multistage amplifier which has one parallel
resonant circuit for every stage, while resonant frequency
of every stage
is slightly different from previous stages.
From circuit diagram it is clear that first stage of this
amplifiers has a resonant circuit formed by L1 & C1 that
f1 = 1 / (2Π √L1 C1)
The o/p of stage is applied to second stage which is tuned
to slightly higher frequency.
f2 = 1 / (2Π √L2 C2)

52.  Second stage amplifiers the signals of frequency
f2 by maximum amplitude while other frequency
signal are amplified by less quantity . Thus frequency
response
 Curve of second stage has a peak of f2 which is
slightly higher than f1.

53. STAGGER TUNED AMPLIFIERS :

54. Over all
response
Freq. response of
first stage
Freq. response of
second stage
f1 f0
f2
Voltage
Frequency
STAGGER TUNED AMPLIFIER

55. STAGGER TUNED AMPLIFIERS
Over all response of these two stage is obtained by
combining individual response & it exhibits a
maximum flatness around the center frequency f0 .
Thus overall bandwidth is better than individual
stage.
Since two stages are in parallel (shunt) & overall
bandwidth is increased thus, it behaves like shunt
circuits for the increased bandwidth.

56. LARGE SIGNAL
(NARROW BAND AMPLIFIER) TUNED
AMPLIFIER
 Single & double stage amplifier are not suitable for
applications involving larger RF power , because of
lower of efficiency of class A operation (single
double) such as for excitation of transmitting antenna.
 For such application larger signal tuned amplifier are
employed because they are operation in class C
operation that has high efficiency & capable of
delivering more power in comparison to that of class
A operation .

57. CIRCUIT DIAGRAM OF LARGE SIGNAL
(NARROW BAND AMPLIFIER) TUNED
AMPLIFIER :+
Vcc
R BVs
C L
C c
R L
C s
Tuned clas s C amplif ier

58.  The resonant tuned circuit is tuned to freq. of i/p
signal . When circuit has a high Q- factor , parallel
resonance occur approximate freq. :
f = 1 / (2 π √LC)
At resonant freq. the impedance of parallel circuit is
very large & purely resistive.
LARGE SIGNAL
(NARROW BAND AMPLIFIER)
TUNED AMPLIFIER

59. LARGE SIGNAL (NARROW BAND
AMPLIFIER) TUNED AMPLIFIER
 Higher the Q of circuit faster gain drops on either side
of resonance freq.
 A large Q leads to small bandwidth equal top sharp
tuning this amplifier has Q>> 10,This means
Bandwidth is less than 10% of fr & for this reason , it
is called as narrow band amplifier.

60. COMPARISON BETWEEN TUNED AND AF
AMPLIFIER
 It has to amplify narrow
band of frequencies
defined by the tuned load
at the collector
 They are bulky and
costlier
 Used in radio transmitters
and receivers, and
television receivers
circuits .
 Works with a complete
audio frequency range
 More compact
 Amplifies sound
signals and act as drive
for loud speakers
Tuned Amplifier AF Amplifier

61. APPLICATIONS OF TUNED AMPLIFIER
Tuned amplifiers serve the best for two purposes:
a)Selection of desired frequency.
b)Amplifying the signal to a desired level.
USED IN:
 Communication transmitters and receivers.
 In filter design :--Band Pass, low pass, High pass
and band reject filter design.

62. ADVANTAGES
 It provides high selectivity.
 It has small collector voltage.
 Power loss is also less.
 Signal to noise ratio of O/P is good.
 They are well suited for radio transmitters and
receivers .

63. DISADVANTAGES
 They are not suitable to amplify audio
frequencies.
 If the band of frequency is increase then design
becomes complex.
 Since they use inductors and capacitors as tuning
elements, the circuit is bulky and costly.

64. Numerical

65. Q-1) A single tuned amplifier consist of tuned circuits having
R=5ohm,L=10mh,c=0.1mf. Determine
a)resonant frequency.
b)quality factor of tank circuit
c)band width of amplifier
Ans - Given data-:
R=50ohm;
L=10mh;
C = 0.1mf

66. We know:
Resonant frequency = 1/ 2 π √[ (1/LC) – (R2 / L2 ) ]
= 1 / 2 π √[(1/10*10-3 - 25/100*10-6)
]
= 5.034 KHz
Q = 2 π * 5.034 * 10-3 * 10 * 10-3 / 5
= 63.227
BW = FR /Q = 5.034 / 63.227
= 79.62KHz
RESULT:- Fr = 5.034 KHz
Q = 63.227
BW = 79.62KHz

67. Q2.In a class c amplifier ckt C=300pf,L=50mH,R=40ohm,
RL =4M ohm.
Determine:-
a)Resonant frequency
b)D.C load
c)A.C load
d)Quality factor
Ans :- Given:
C=300pf
L=50mH
R=40ohm
RL =4M ohm

68. Fr = 1/2 π √ LC
= 1/2 π √(50 * 10-6 * 300 * 10 -12 )
= 1.3 MHz
Rdc = 40 ohm
XL = 2 π fr L
= 2* 3.14 * 1.3 * 106 * 50 * 10-6
= 408.2
Qdc = 408.2/ 40
= 10.205

69. Rac = Rp ll RL
Rp = Qdc * XL
= 10.205 * 408.2
= 4165.681
RL = 4* 106
Rac = 4161.34
Qac = [Rac / XL ]
= 4161.34/408.2
= 10.194
Result: -
Fr = 1.3 MHz
Qdc = 10.205
Qac = 10.194

70. Q. A circuit is resonant resonant at 455 khz and has a 10khz
bandwidth. The inductive reactance is 1255ohm. What is the
parallel impedance of the circuit at resonance?
Solution:
Given that:
fr =455 khz
Frequency BW=10khz and XL
Let zp be the value of impedance at resonance
We know that the value of bandwidth
(BW)=fr /Q
So, 10*103 =455*103 /Q
Q=45.5
Q=XL /R
XL =1255

71. 1255=2∏fr L=2859*103 L
L=1255/(2859*103)
L=.439*103 H
Value of capacitance reactance at resonance:
XC =XL
=1255Ω
1/2∏fr = 1255
Therefore, C=278.7*10-12 F
And value of circuit impedance at resonance
zp =L/CR
=0.439*103 / (278.7*10-12)*27.6
=57*103
=57 kΩ
RESULT: the parallel impedance at resonance is 57kΩ.

72. Q: A FET has gm=6 mA/v, has a tuned anode load
consisting of a 400 microH inductance of 5 ohm in parallal
with a capacitor of 2500pf. Find:-
1. The resonant frequency
2. Tuned circuit dynamic resistance
3. Gain at resonance
4. The signal bandwidth
Solution:-
1. Fr => resonant frequency
= 1/(2π√(LC))
= 0.159/ √ (400*2500)
= 1.59*105 Hz = 0.159 MHz
2. Rd => tuned circuit dynamic resistance
= L/CR
= 400/(2500*5)

73. = 106 * 80/2500
= 0.032 * 106
= 32 k ohm
3. Av = -gm rd = 6*32 = -192
4. BW= fr / Q
Q = Wr L/ R
= (2 π * 0.159 * 10 -6 * 400 * 106) / 5 = 79.92
BW = 0.159/ 79.92
= 1.98 KHz
RESULT:
Resonant frequency=0.159MHz
Dynamic Resistance=32kΩ
Resonance gain=-192
Bandwidth=1.98khz

74. Q: A tuned voltage amplifier, using FET with rd = 100 kohm and
gm = 500 micro s has tuned circuit, consisting of L= 2.5 mH , C =
200 pF , as its load. At its resonant frequency , the circuit offers an
equivalent shunt resistance of 100 kohm. For the amplifier
determine:-
1. Resonant gain
2. The effective Q
3. The Bandwidth
Solution: -
Given that: gm= 500
Shunt resistance=100 kohm
1. Resonant gain:-
Av = -gm (rd ll Rd )/(1 + jf/fr)
Av = 500(100 ll 100)/(1 + j1)
Av = 17.68

75. 2. Effective Q: -
Qeff = L/CR
R = 100 ll 100
Q = 2.5* 103 /(200*10-12 * 50 * 103)
= 2.5 * 102
3. Bandwidth: -
BW = fr /Qeff
fr = 1/2 π √ LC
= 225 kHz
BW = 225/ 2.5* 102
= 900 Hz
RESULT:
Resonant gain=17.68
Qeff =2.5*102
BW = 900 Hz

76. Submitted By:
Rakesh mandiya