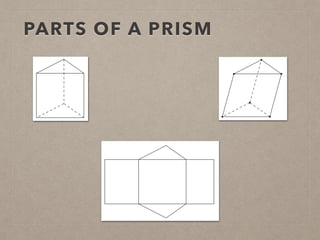
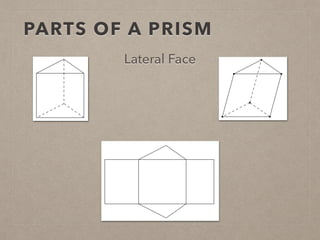
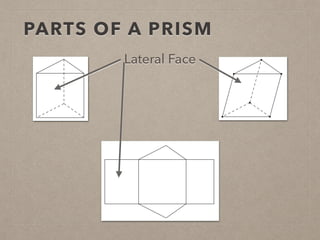
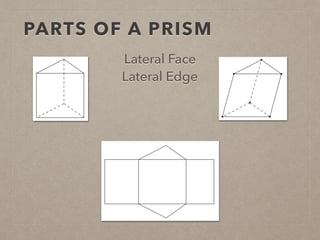
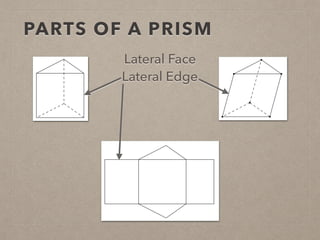
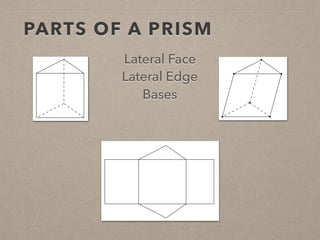
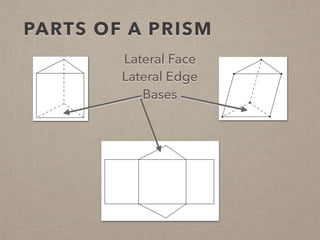
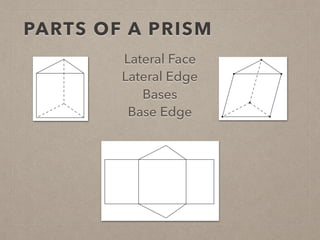
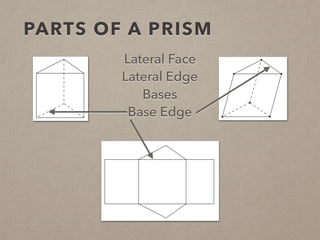
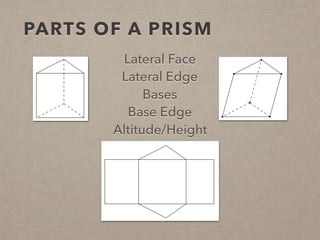
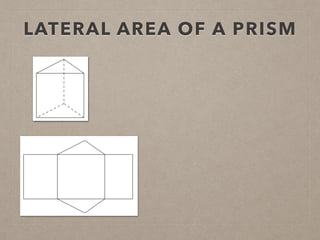
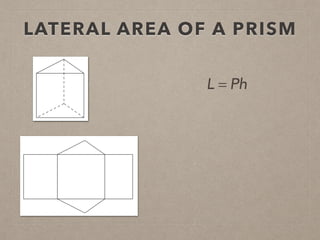
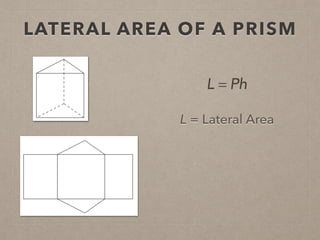
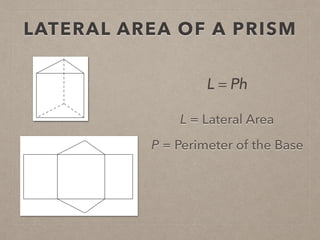
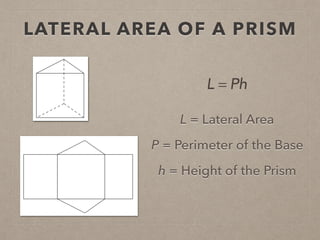
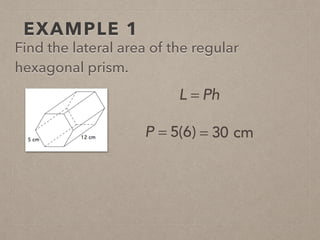
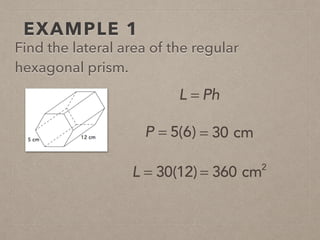
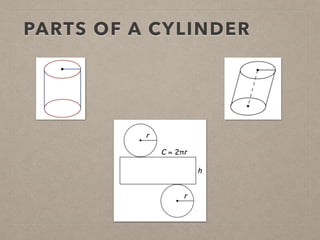
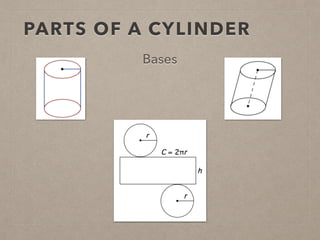
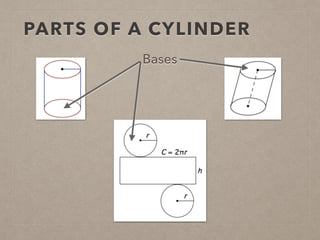
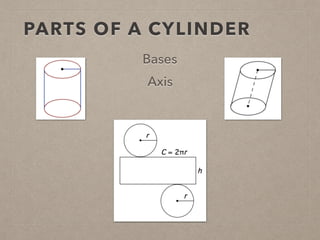
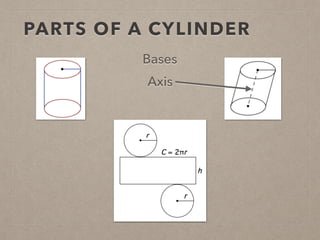
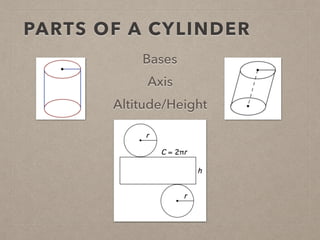
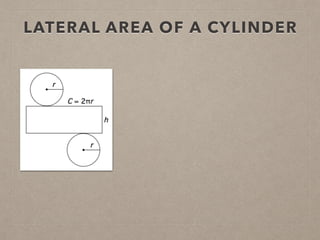
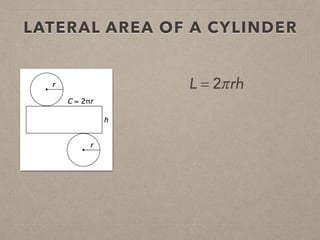
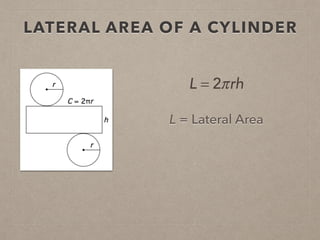
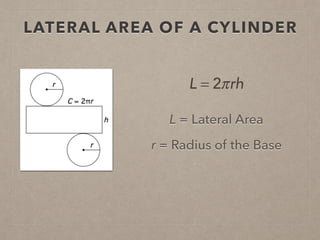
This document provides information on calculating the surface areas of prisms and cylinders. It defines key terms like lateral face, base edge, and altitude. It explains that the lateral area of a prism is calculated as P*h, where P is the perimeter of the base and h is the height. The surface area of a prism is the lateral area plus twice the area of the base. For cylinders, the lateral area is 2πrh, where r is the radius and h is the height. The surface area of a cylinder is the lateral area plus twice the area of the circular base. Examples are provided to demonstrate calculating lateral and surface areas.

1. SECTION 12-2
SURFACE AREAS OF PRISMS AND
CYLINDERS

2. ESSENTIAL QUESTIONS
• How do you find lateral areas and
surface areas of prisms?
• How do you find lateral areas and
surface areas of cylinders?

3. VOCABULARY
1. Lateral Face:
2. Lateral Edge:
3. Base Edge:
4. Altitude:

4. VOCABULARY
1. Lateral Face:
2. Lateral Edge:
3. Base Edge:
4. Altitude:
The surfaces of a polyhedron
that are not bases

5. VOCABULARY
1. Lateral Face:
2. Lateral Edge:
3. Base Edge:
4. Altitude:
The surfaces of a polyhedron
that are not bases
Formed where the lateral
faces intersect

6. VOCABULARY
1. Lateral Face:
2. Lateral Edge:
3. Base Edge:
4. Altitude:
The surfaces of a polyhedron
that are not bases
Formed where the lateral
faces intersect
Formed where the lateral faces
intersect the base(s)

7. VOCABULARY
1. Lateral Face:
2. Lateral Edge:
3. Base Edge:
4. Altitude:
The surfaces of a polyhedron
that are not bases
Formed where the lateral
faces intersect
Formed where the lateral faces
intersect the base(s)
The perpendicular segment that
joins the bases of a prism/cylinder

8. VOCABULARY
5. Height:
6: Lateral Area:
7. Axis:

9. VOCABULARY
5. Height:
6: Lateral Area:
7. Axis:
Another word for the altitude of a
prism/cylinder

10. VOCABULARY
5. Height:
6: Lateral Area:
7. Axis:
Another word for the altitude of a
prism/cylinder
The sum of the areas of the
lateral faces

11. VOCABULARY
5. Height:
6: Lateral Area:
7. Axis:
Another word for the altitude of a
prism/cylinder
The sum of the areas of the
lateral faces
In a cylinder, this is the segment whose
endpoints are the centers of the circular
bases

12. PARTS OF A PRISM

13. PARTS OF A PRISM
Lateral Face

14. PARTS OF A PRISM
Lateral Face

15. PARTS OF A PRISM
Lateral Face
Lateral Edge

16. PARTS OF A PRISM
Lateral Face
Lateral Edge

17. PARTS OF A PRISM
Lateral Face
Lateral Edge
Bases

18. PARTS OF A PRISM
Lateral Face
Lateral Edge
Bases

19. PARTS OF A PRISM
Lateral Face
Lateral Edge
Base Edge
Bases

20. PARTS OF A PRISM
Lateral Face
Lateral Edge
Base Edge
Bases

21. PARTS OF A PRISM
Lateral Face
Lateral Edge
Base Edge
Altitude/Height
Bases

22. LATERAL AREA OF A PRISM

23. LATERAL AREA OF A PRISM
L = Ph

24. LATERAL AREA OF A PRISM
L = Lateral Area
L = Ph

25. LATERAL AREA OF A PRISM
L = Lateral Area
P = Perimeter of the Base
L = Ph

26. LATERAL AREA OF A PRISM
L = Lateral Area
P = Perimeter of the Base
h = Height of the Prism
L = Ph

27. EXAMPLE 1
Find the lateral area of the regular
hexagonal prism.

28. EXAMPLE 1
Find the lateral area of the regular
hexagonal prism.
L = Ph

29. EXAMPLE 1
Find the lateral area of the regular
hexagonal prism.
L = Ph
P = 5(6)

30. EXAMPLE 1
Find the lateral area of the regular
hexagonal prism.
L = Ph
P = 5(6) = 30 cm

31. EXAMPLE 1
Find the lateral area of the regular
hexagonal prism.
L = Ph
P = 5(6) = 30 cm
L = 30(12)

32. EXAMPLE 1
Find the lateral area of the regular
hexagonal prism.
L = Ph
P = 5(6) = 30 cm
L = 30(12) = 360 cm2

33. SURFACE AREA OF A PRISM

34. SURFACE AREA OF A PRISM
SA = L + 2B or SA= Ph + 2B

35. SURFACE AREA OF A PRISM
L = Lateral Area
SA = L + 2B or SA= Ph + 2B

36. SURFACE AREA OF A PRISM
L = Lateral Area
P = Perimeter of the Base
SA = L + 2B or SA= Ph + 2B

37. SURFACE AREA OF A PRISM
L = Lateral Area
P = Perimeter of the Base
SA = L + 2B or SA= Ph + 2B
B = Area of the Base

38. SURFACE AREA OF A PRISM
L = Lateral Area
P = Perimeter of the Base
h = height of the prism
SA = L + 2B or SA= Ph + 2B
B = Area of the Base

39. EXAMPLE 2
Find the surface area of the rectangular
prism.

40. EXAMPLE 2
Find the surface area of the rectangular
prism.
SA = L + 2B

41. EXAMPLE 2
Find the surface area of the rectangular
prism.
SA = 4(6)(10) + 2(6)(6)
SA = L + 2B

42. EXAMPLE 2
Find the surface area of the rectangular
prism.
SA = 4(6)(10) + 2(6)(6)
SA = 312 in2
SA = L + 2B

43. PARTS OF A CYLINDER

44. PARTS OF A CYLINDER
Bases

45. PARTS OF A CYLINDER
Bases

46. PARTS OF A CYLINDER
Bases
Axis

47. PARTS OF A CYLINDER
Bases
Axis

48. PARTS OF A CYLINDER
Bases
Axis
Altitude/Height

49. LATERAL AREA OF A CYLINDER

50. LATERAL AREA OF A CYLINDER
L = 2πrh

51. LATERAL AREA OF A CYLINDER
L = Lateral Area
L = 2πrh

52. LATERAL AREA OF A CYLINDER
L = Lateral Area
r = Radius of the Base
L = 2πrh

53. LATERAL AREA OF A CYLINDER
L = Lateral Area
r = Radius of the Base
h = Height of the Cylinder
L = 2πrh

54. SURFACE AREA OF A
CYLINDER

55. SURFACE AREA OF A
CYLINDER
SA = L + 2B or SA = 2πrh + 2πr2

56. SURFACE AREA OF A
CYLINDER
L = Lateral Area
SA = L + 2B or SA = 2πrh + 2πr2

57. SURFACE AREA OF A
CYLINDER
L = Lateral Area
SA = L + 2B or SA = 2πrh + 2πr2
B = Area of the Base

58. SURFACE AREA OF A
CYLINDER
L = Lateral Area
r = Radius of the Base
SA = L + 2B or SA = 2πrh + 2πr2
B = Area of the Base

59. SURFACE AREA OF A
CYLINDER
L = Lateral Area
r = Radius of the Base
h = Height of the Cylinder
SA = L + 2B or SA = 2πrh + 2πr2
B = Area of the Base

60. EXAMPLE 3
Find the lateral area and the surface
area of the cylinder. Round to the
nearest hundredth.

61. EXAMPLE 3
Find the lateral area and the surface
area of the cylinder. Round to the
nearest hundredth.
L = 2πrh

62. EXAMPLE 3
Find the lateral area and the surface
area of the cylinder. Round to the
nearest hundredth.
L = 2πrh
L = 2π(14)(18)

63. EXAMPLE 3
Find the lateral area and the surface
area of the cylinder. Round to the
nearest hundredth.
L = 2πrh
L = 2π(14)(18)
L ≈ 1583.36 ft2

64. EXAMPLE 3
Find the lateral area and the surface
area of the cylinder. Round to the
nearest hundredth.

65. EXAMPLE 3
Find the lateral area and the surface
area of the cylinder. Round to the
nearest hundredth.
SA = L + 2B

66. EXAMPLE 3
Find the lateral area and the surface
area of the cylinder. Round to the
nearest hundredth.
SA = L + 2B
SA = 2πrh + 2πr2

67. EXAMPLE 3
Find the lateral area and the surface
area of the cylinder. Round to the
nearest hundredth.
SA = L + 2B
SA = 2π(14)(18) + 2π(14)2
SA = 2πrh + 2πr2

68. EXAMPLE 3
Find the lateral area and the surface
area of the cylinder. Round to the
nearest hundredth.
SA = L + 2B
SA = 2π(14)(18) + 2π(14)2
SA = 504π + 392π
SA = 2πrh + 2πr2

69. EXAMPLE 3
Find the lateral area and the surface
area of the cylinder. Round to the
nearest hundredth.
SA = L + 2B
SA = 2π(14)(18) + 2π(14)2
SA = 504π + 392π
SA = 896π
SA = 2πrh + 2πr2

70. EXAMPLE 3
Find the lateral area and the surface
area of the cylinder. Round to the
nearest hundredth.
SA = L + 2B
SA = 2π(14)(18) + 2π(14)2
SA = 504π + 392π
SA = 896π ≈ 2814.87 ft2
SA = 2πrh + 2πr2

71. PROBLEM SET

72. PROBLEM SET
p. 833 #1-23 odd
“No act of kindness, no matter how small, is
ever wasted.” - Aesop