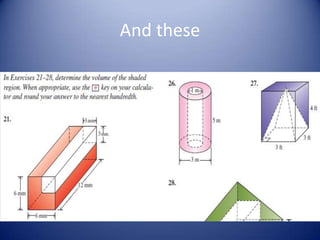
The document summarizes formulas for calculating the volume and surface area of basic three-dimensional geometric shapes like prisms, pyramids, cylinders, and cones. It provides the general volume formulas for prisms and pyramids, which are used to calculate the volume of rectangular and circular prisms. The surface area formulas are also outlined, explaining that surface area is the total two-dimensional area on the outside of a three-dimensional figure, calculated by finding the area of each face and adding them together. Examples are worked through applying the formulas to specific shapes with given dimensions.

1. Volume & Surface Area
of Three-Dimensional Figures
What’s it all about?

2. Volume
• Volume is the three-dimensional space taken
up by a polyhedron (solid figure).
• It is measured in cubic units

3. Volume Formulas
There are two general formulas we use for the two basic shapes
of three-dimensional figures:
PRISMS & PYRAMIDS
Prisms go straight up Pyramids come to a
from their Base to a point

4. Volume Formulas for Prisms
• In general, the Volume formulas
for any Prism is
V = Bh
where B is the area of the Base
Rectangular Base Round Base
A = lw A = r 2

5. Let’s try one
V = Bh or lwh
V = (8)(3)(4)
V = 96 ft cubed

6. Now try this one
Find the volume of a rectangular solid (prism)
shed
Length: 5.5 feet Width: 7 feet Height: 9 feet
If the grain to be stored in this shed sells for
$ 15 per cubic foot, how much can the whole
shed sell for?

7. Answer
• A = lwh
• A = (5.5)(7)(9)
• A = 346.5 cubic feet
• 346.5 x $15 = $5197.50

8. Cylinders work the same way
V = Bh or r h
2
Area of the Circular Base is =
(3.14) (5)^2
And then times the height
V = (78.5)(9) = 706.5 cubic ins

9. Again, you try one
1. Find the volume of a cylinder (circular prism)
with the following dimensions:
Radius of the circular base is 4 feet,
height is 10 feet. How much grain can it hold?
2. What if a supporting pole with a radius of one
foot ran down the center of this flat silo?
Then how much grain could it hold?

10. Answer
1) Volume of the original cylinder
V = (3.14)(4)^2 (10) = 502.4 cubic feet
2) Volume of the pole
V = 3.14 (1)^2 (10) = 31.4 cubic feet
3) New Volume
502. 4 – 31.4 = 471 cubic feet

11. Now let’s look at the Volume of
Pyramids (& cones)
Their general formula is:
V = 1/3 Bh
We can take the previous examples and just
divide their volume by 3. Given the same
height and Base, the volume of pyramids and
cones are 1/3 the correspondingly sized
prisms.
V = (1/3)(3.14)(3)^2(4)
V = 37.68 cubic meters

12. Surface Area
Surface Area is two-dimensional.
It is the amount of coverage on the outside of
the figure. It includes the top, bottom, and
lateral sides.

13. Rectangular Solids are easy
Add the surface areas of all six sides of this prism to get
its total surface area.
Top & Bottom: A = (8)(3) = 24*2 = 48 square feet
Front & Back: A = (8)(4) = 32*2 = 64 square feet
Left & Right: A = (4)(3) = 12*2 = 24 square feet
48+64+24 = 136 square feet total surface area

14. Surface Area of Square Pyramids
For any three-dimensional figure, study the shapes that
make up the top, bottom & sides.
Calculate the areas for each of these shapes
separately and add them together at the end.
What shapes do you see? How many?
Side of Square base: 5 Slant height of each triangle: 8
Area of Base = 25
Area of triangle = (1/2)(5)(8) = 20
Area of 4 lateral sides = 80
Total Surface Area = 80+25 = 105 sq ins

15. And now the Surface Area of the
Cylinder
Calculate the top & bottom separately from the
lateral side, and then add them together.
Area of circular bases: 2(3.14)(r)^2
Area of the lateral side is the circumference of
the circular base * height

16. Let’s put some numbers in
For this cylinder: Radius = 6 and Height = 8
Area of Top & Bottom: 2(3.14)(6)^2 = 226.08
Area of Lateral Side: (12)(3.14)(8) = 301.44
226.08 + 301.44 = 527.52 square units

17. Now you try
Find the surface area of a cylinder with a radius
of 3.5 inches and a height of 5 inches.

18. Answer
Area of top & Bottom: 2(3.14)(3.5)^2 = 76.93
Area of lateral side: (3.14)(7)(5) = 109.9
Add: 76.93 + 109.9 = 186.83 square units

19. Go for this from your book

20. And these