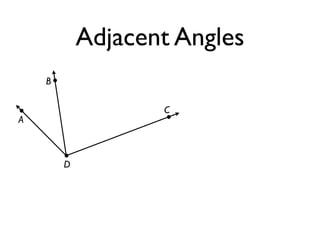
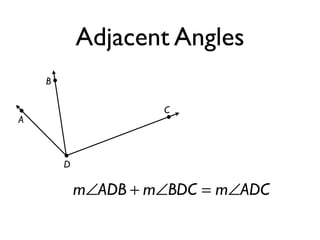
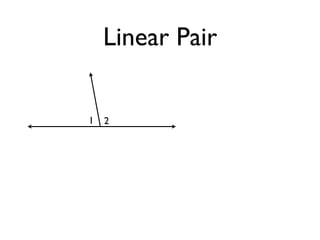
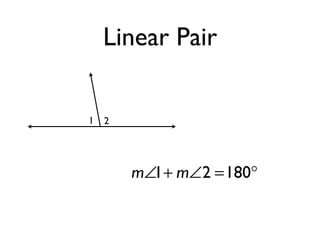
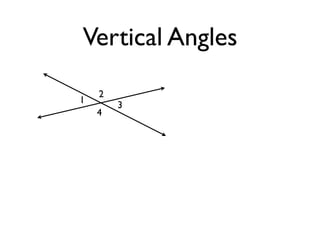
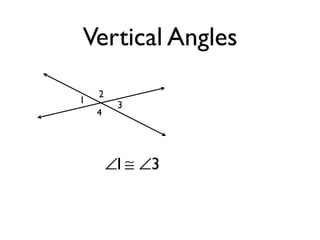
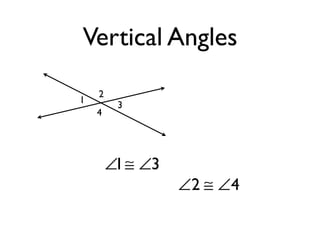
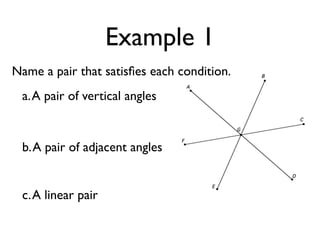
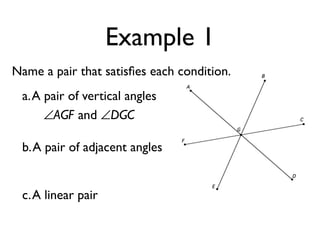
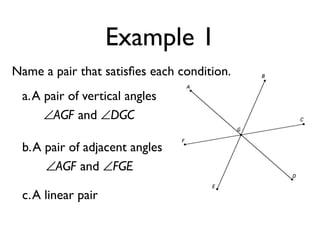
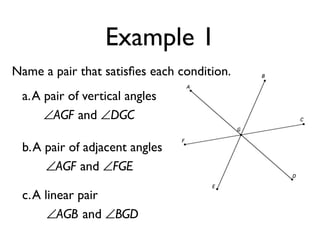
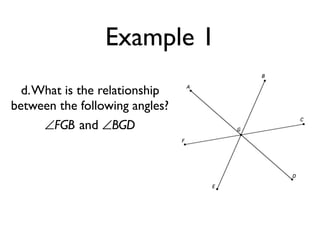
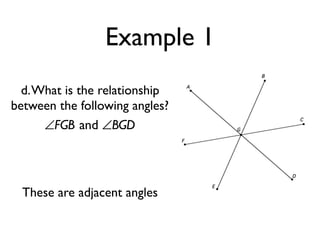
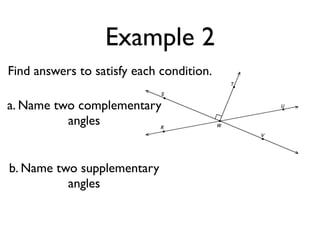
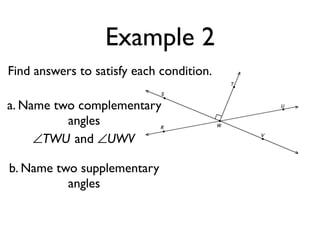
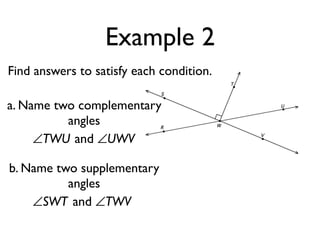
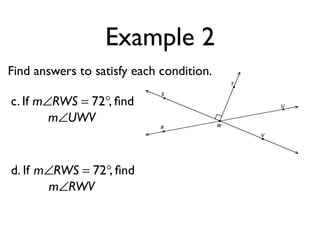
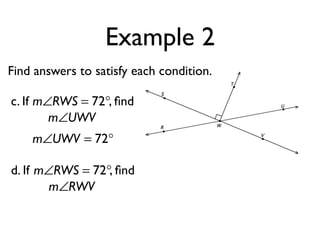
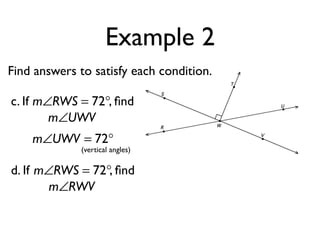
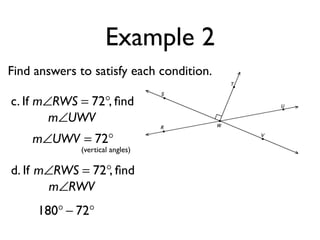
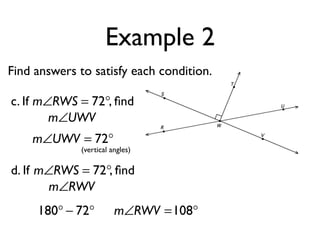
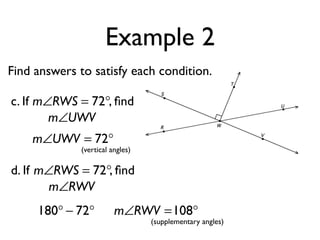
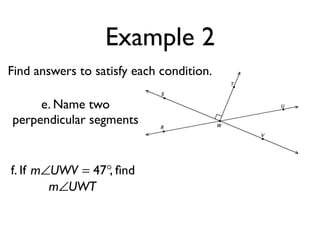
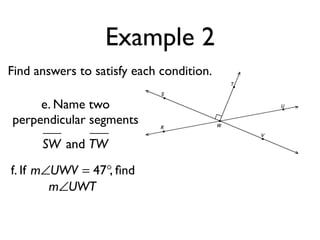
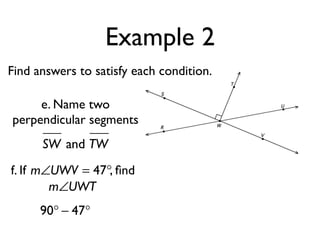
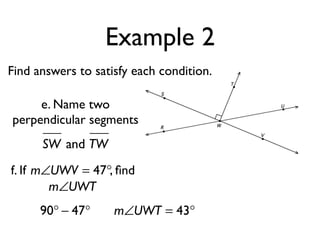
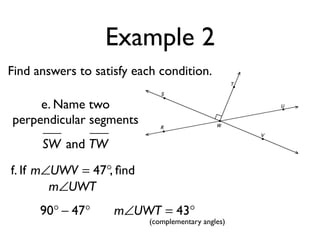
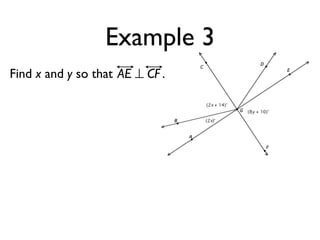
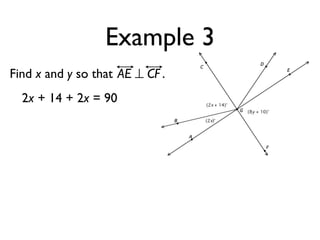
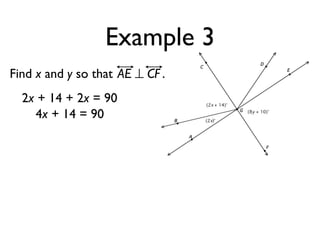
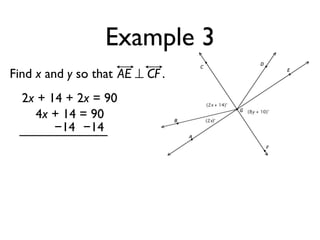
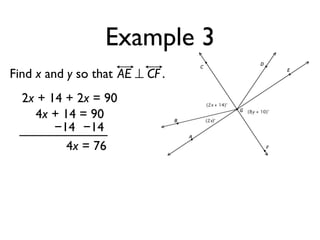
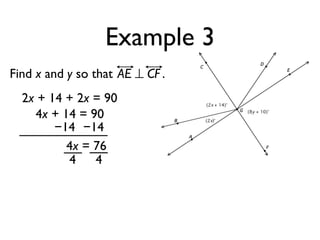
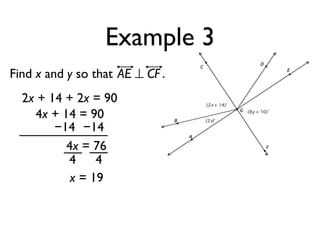
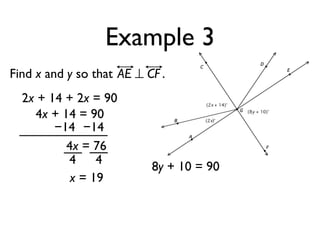
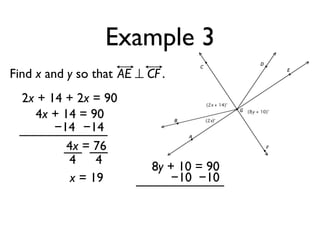
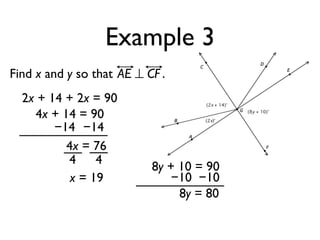
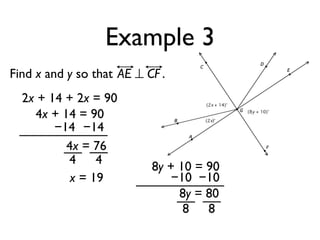
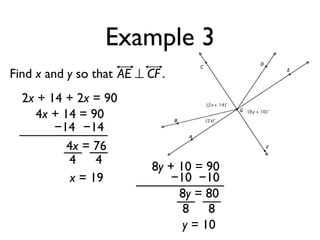
The document defines and provides examples of angle relationships including adjacent angles, linear pairs, vertical angles, complementary angles, and supplementary angles. It defines each term and provides examples of identifying angle pairs that satisfy each relationship. It also includes examples of using properties of these angle relationships to solve problems, such as finding missing angle measures.

1. Section 1-5
Angle Relationships

2. Essential Questions
• How do you identify and use special pairs
of angles?
• How do you identify perpendicular lines?

3. Vocabulary
1. Adjacent Angles:
2. Linear Pair:
3. Vertical Angles:
4. Complementary Angles:

4. Vocabulary
1. Adjacent Angles: Two angles that share a vertex and
side but no interior points
2. Linear Pair:
3. Vertical Angles:
4. Complementary Angles:

5. Vocabulary
1. Adjacent Angles: Two angles that share a vertex and
side but no interior points
2. Linear Pair: A pair of adjacent angles where the non-
shared sides are opposite rays
3. Vertical Angles:
4. Complementary Angles:

6. Vocabulary
1. Adjacent Angles: Two angles that share a vertex and
side but no interior points
2. Linear Pair: A pair of adjacent angles where the non-
shared sides are opposite rays
3. Vertical Angles: Nonadjacent angles that are formed
when two lines intersect; only share a vertex
4. Complementary Angles:

7. Vocabulary
1. Adjacent Angles: Two angles that share a vertex and
side but no interior points
2. Linear Pair: A pair of adjacent angles where the non-
shared sides are opposite rays
3. Vertical Angles: Nonadjacent angles that are formed
when two lines intersect; only share a vertex
4. Complementary Angles: Two angles with measures
such that the sum of the angles is 90 degrees

8. Vocabulary
5. Supplementary Angles:
6. Perpendicular:

9. Vocabulary
5. Supplementary Angles: Two angles with measures
such that the sum of the angles is 180 degrees
6. Perpendicular:

10. Vocabulary
5. Supplementary Angles: Two angles with measures
such that the sum of the angles is 180 degrees
6. Perpendicular: When two lines, segments, or rays
intersect at a right angle

11. Adjacent Angles

12. Adjacent Angles
A
B
C
D

13. Adjacent Angles
A
B
C
D
m∠ADB + m∠BDC = m∠ADC

14. Linear Pair

15. Linear Pair
1 2

16. Linear Pair
1 2
m∠1+ m∠2 =180°

17. Vertical Angles

18. Vertical Angles
1
2
3
4

19. Vertical Angles
∠1≅ ∠3
1
2
3
4

20. Vertical Angles
∠1≅ ∠3
1
2
3
4
∠2 ≅ ∠4

21. Example 1
Name a pair that satisfies each condition.
a.A pair of vertical angles
b.A pair of adjacent angles
c.A linear pair

22. Example 1
Name a pair that satisfies each condition.
a.A pair of vertical angles
∠AGF and ∠DGC
b.A pair of adjacent angles
c.A linear pair

23. Example 1
Name a pair that satisfies each condition.
a.A pair of vertical angles
∠AGF and ∠DGC
b.A pair of adjacent angles
∠AGF and ∠FGE
c.A linear pair

24. Example 1
Name a pair that satisfies each condition.
a.A pair of vertical angles
∠AGF and ∠DGC
b.A pair of adjacent angles
∠AGF and ∠FGE
c.A linear pair
∠AGB and ∠BGD

25. Example 1
d.What is the relationship
between the following angles?
∠FGB and ∠BGD

26. Example 1
d.What is the relationship
between the following angles?
∠FGB and ∠BGD
These are adjacent angles

27. Example 2
Find answers to satisfy each condition.
a. Name two complementary
angles
b. Name two supplementary
angles

28. Example 2
Find answers to satisfy each condition.
a. Name two complementary
angles
∠TWU and ∠UWV
b. Name two supplementary
angles

29. Example 2
Find answers to satisfy each condition.
a. Name two complementary
angles
∠TWU and ∠UWV
b. Name two supplementary
angles
∠SWT and ∠TWV

30. Example 2
Find answers to satisfy each condition.
c. If , findm∠RWS = 72°
m∠UWV
d. If , findm∠RWS = 72°
m∠RWV

31. Example 2
Find answers to satisfy each condition.
m∠UWV = 72°
c. If , findm∠RWS = 72°
m∠UWV
d. If , findm∠RWS = 72°
m∠RWV

32. Example 2
Find answers to satisfy each condition.
m∠UWV = 72°
c. If , findm∠RWS = 72°
m∠UWV
(vertical angles)
d. If , findm∠RWS = 72°
m∠RWV

33. Example 2
Find answers to satisfy each condition.
m∠UWV = 72°
c. If , findm∠RWS = 72°
m∠UWV
(vertical angles)
d. If , findm∠RWS = 72°
m∠RWV
180° − 72°

34. Example 2
Find answers to satisfy each condition.
m∠UWV = 72°
c. If , findm∠RWS = 72°
m∠UWV
(vertical angles)
m∠RWV =108°
d. If , findm∠RWS = 72°
m∠RWV
180° − 72°

35. Example 2
Find answers to satisfy each condition.
m∠UWV = 72°
c. If , findm∠RWS = 72°
m∠UWV
(vertical angles)
m∠RWV =108°
d. If , findm∠RWS = 72°
m∠RWV
(supplementary angles)
180° − 72°

36. Example 2
Find answers to satisfy each condition.
f. If , findm∠UWV = 47°
m∠UWT
e. Name two
perpendicular segments

37. Example 2
Find answers to satisfy each condition.
SW and TW
f. If , findm∠UWV = 47°
m∠UWT
e. Name two
perpendicular segments

38. Example 2
Find answers to satisfy each condition.
SW and TW
f. If , findm∠UWV = 47°
m∠UWT
90° − 47°
e. Name two
perpendicular segments

39. Example 2
Find answers to satisfy each condition.
SW and TW
m∠UWT = 43°
f. If , findm∠UWV = 47°
m∠UWT
90° − 47°
e. Name two
perpendicular segments

40. Example 2
Find answers to satisfy each condition.
SW and TW
m∠UWT = 43°
f. If , findm∠UWV = 47°
m∠UWT
(complementary angles)
90° − 47°
e. Name two
perpendicular segments

41. Example 3
Find x and y so that AE ⊥ CF .

42. Example 3
Find x and y so that AE ⊥ CF .
2x + 14 + 2x = 90

43. Example 3
Find x and y so that AE ⊥ CF .
2x + 14 + 2x = 90
4x + 14 = 90

44. Example 3
Find x and y so that AE ⊥ CF .
2x + 14 + 2x = 90
4x + 14 = 90
−14 −14

45. Example 3
Find x and y so that AE ⊥ CF .
2x + 14 + 2x = 90
4x + 14 = 90
−14 −14
4x = 76

46. Example 3
Find x and y so that AE ⊥ CF .
2x + 14 + 2x = 90
4x + 14 = 90
−14 −14
4x = 76
4 4

47. Example 3
Find x and y so that AE ⊥ CF .
2x + 14 + 2x = 90
4x + 14 = 90
−14 −14
4x = 76
4 4
x = 19

48. Example 3
Find x and y so that AE ⊥ CF .
2x + 14 + 2x = 90
4x + 14 = 90
−14 −14
4x = 76
4 4
x = 19
8y + 10 = 90

49. Example 3
Find x and y so that AE ⊥ CF .
2x + 14 + 2x = 90
4x + 14 = 90
−14 −14
4x = 76
4 4
x = 19
8y + 10 = 90
−10 −10

50. Example 3
Find x and y so that AE ⊥ CF .
2x + 14 + 2x = 90
4x + 14 = 90
−14 −14
4x = 76
4 4
x = 19
8y + 10 = 90
−10 −10
8y = 80

51. Example 3
Find x and y so that AE ⊥ CF .
2x + 14 + 2x = 90
4x + 14 = 90
−14 −14
4x = 76
4 4
x = 19
8y + 10 = 90
−10 −10
8y = 80
8 8

52. Example 3
Find x and y so that AE ⊥ CF .
2x + 14 + 2x = 90
4x + 14 = 90
−14 −14
4x = 76
4 4
x = 19
8y + 10 = 90
−10 −10
8y = 80
8 8
y = 10

53. Example 4
Find the measures of two supplementary angles so that
the difference between the measures of the two angles
is 44.
x° (180 − x)°

54. Example 4
Find the measures of two supplementary angles so that
the difference between the measures of the two angles
is 44.
x° (180 − x)°
(180 − x) − x = 44

55. Example 4
Find the measures of two supplementary angles so that
the difference between the measures of the two angles
is 44.
x° (180 − x)°
(180 − x) − x = 44
180 − 2x = 44

56. Example 4
Find the measures of two supplementary angles so that
the difference between the measures of the two angles
is 44.
x° (180 − x)°
(180 − x) − x = 44
180 − 2x = 44
−180 −180

57. Example 4
Find the measures of two supplementary angles so that
the difference between the measures of the two angles
is 44.
x° (180 − x)°
(180 − x) − x = 44
180 − 2x = 44
−180 −180
−2x = −136

58. Example 4
Find the measures of two supplementary angles so that
the difference between the measures of the two angles
is 44.
x° (180 − x)°
(180 − x) − x = 44
180 − 2x = 44
−180 −180
−2x = −136
−2 −2

59. Example 4
Find the measures of two supplementary angles so that
the difference between the measures of the two angles
is 44.
x° (180 − x)°
(180 − x) − x = 44
180 − 2x = 44
−180 −180
−2x = −136
−2 −2
x = 68°

60. Example 4
Find the measures of two supplementary angles so that
the difference between the measures of the two angles
is 44.
x° (180 − x)°
(180 − x) − x = 44
180 − 2x = 44
−180 −180
−2x = −136
−2 −2
x = 68°
180 − 68

61. Example 4
Find the measures of two supplementary angles so that
the difference between the measures of the two angles
is 44.
x° (180 − x)°
(180 − x) − x = 44
180 − 2x = 44
−180 −180
−2x = −136
−2 −2
x = 68°
180 − 68 =112°

62. Example 4
Find the measures of two supplementary angles so that
the difference between the measures of the two angles
is 44.
x° (180 − x)°
(180 − x) − x = 44
180 − 2x = 44
−180 −180
−2x = −136
−2 −2
x = 68°
180 − 68 =112°
The two angles are 68°
and 112°