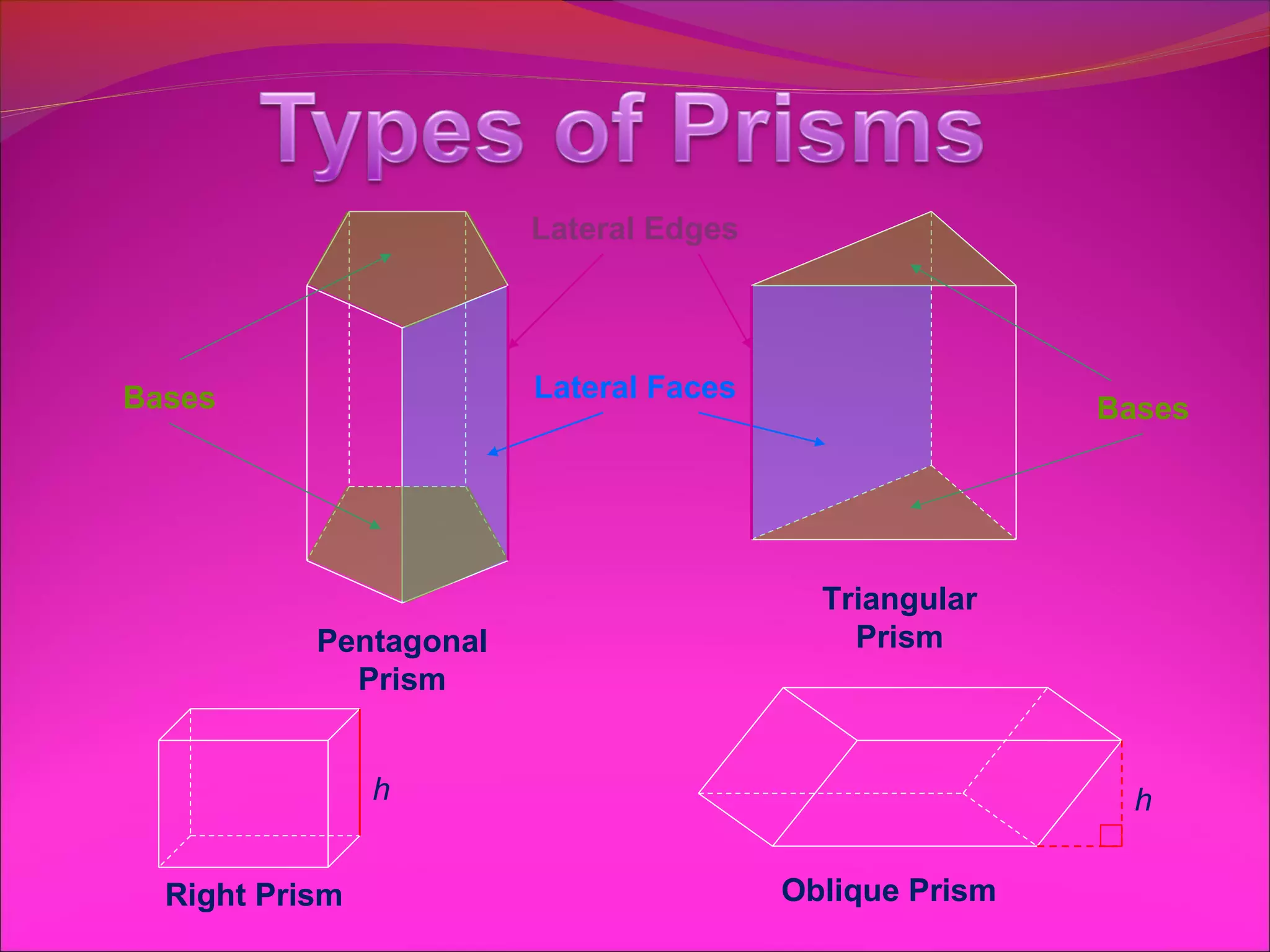
Students learn formulas to compute the volumes and surface areas of prisms, pyramids, cylinders, cones, and spheres. The document provides formulas to find the lateral area, base area, and total surface area of prisms and cylinders. It includes examples of using the formulas to find the surface area of regular hexagonal and triangular prisms, and cylinders with given heights and radii.

2. Students compute the volumes and surface areas of
prisms, pyramids, cylinders, cones, and spheres;
and students commit to memory the formulas for
prisms, pyramids, and cylinders.

3. Lateral Edges
Bases Lateral Faces
Bases
Triangular
Pentagonal Prism
Prism
h h
Right Prism Oblique Prism

4. Lateral Area and Surface Area of a Prism
Base Perimeter
h
L = Ph
Lateral Base Height
Area Perimeter
Base Area
S = L + 2B
Surface Lateral Base Area
Area Area

5. Find the surface area of the regular hexagonal
prism.
S = L + 2B
L = Ph 1 P = 36
L = 432 m B = 2 .5
B = 93apm 2
2
P = 6(6) = 36
S = 432 + 2(93.5)
1
( )
12 m
L = 36(12) B = 3 3 ( 36 )
6m
360 60
S = 432 + 187 2 6
= = 30
2
L = 432 m 2
30
S = 619 m B = 54 3
2 3 3m
B = 93.5 m 2 3m
60

6. Find the surface area of the
triangular prism.
S = L + 2B
1
L = Ph B = bh 12 cm
2
L = 16(12) B = 0.5(6)(4) 5 cm 6 cm
P = 16
L = 192 cm 2
B = 12 cm 2 5 cm
32 + h 2 = 5 2
S = 192 + 2(12) 5 cm
9 + h 2 = 25
h
h 2 = 16
S = 216 cm 2
3 cm
h=4

7. Lateral Area and Surface Area of a Cylinder
L = 2πrh
Base Area
Radius
Lateral Radius Height
h Area
S = L + 2B
Surface
Area
Lateral
Area B = πr
Base Area 2

8. Find the surface area of a cylinder with 5 cm
height 10 cm and radius 5 cm in terms of
pi.
10 cm
S = L + 2B
L = 2πrh B = πr 2
L = 2π (5)(10) B = π (5) 2
L = 100π cm 2
B = 25π cm 2
S = 100π + 2(25π ) S = 150π cm 2

9. Find the surface area of a cylinder with
radius 6 ft and height 9 ft in terms of pi.
9 ft
S = L + 2B
L = 2πrh B = πr 2 6 ft
L = 2π (6)(9) B = π ( 6) 2
L = 108π ft 2
B = 36π ft 2
S = 108π + 2(36π ) S = 180π ft 2

10. Find the surface area of a cylinder with
radius 6 ft and height 9 ft in terms of pi.
9 ft
S = L + 2B
L = 2πrh B = πr 2 6 ft
L = 2π (6)(9) B = π ( 6) 2
L = 108π ft 2
B = 36π ft 2
S = 108π + 2(36π ) S = 180π ft 2