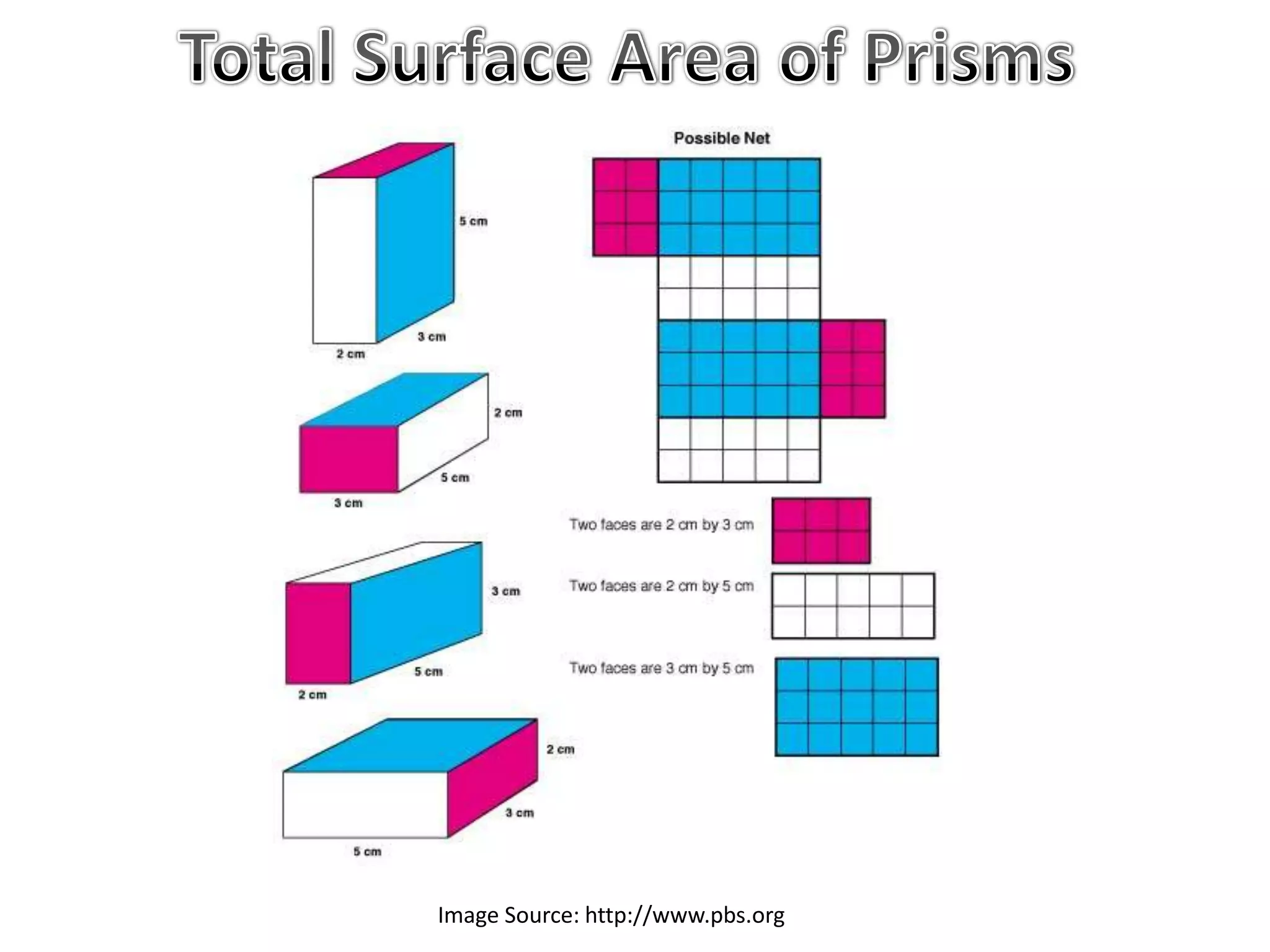
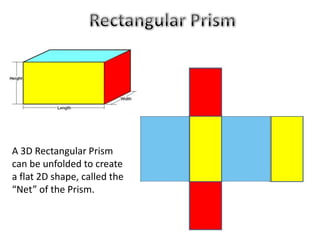
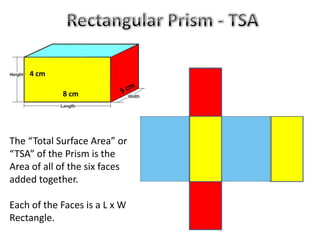
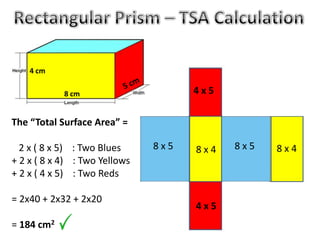
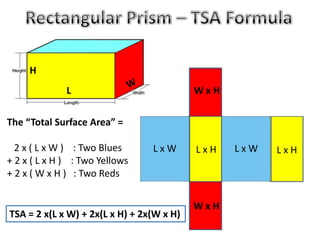
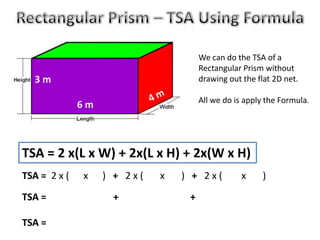
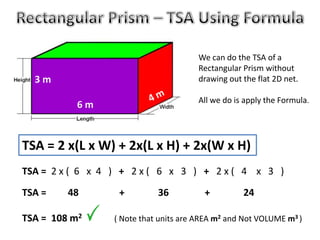
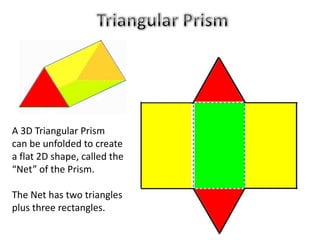
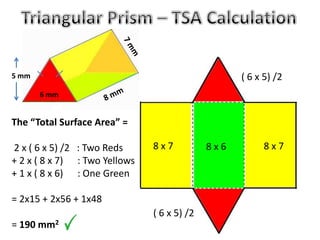
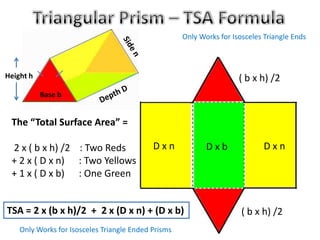
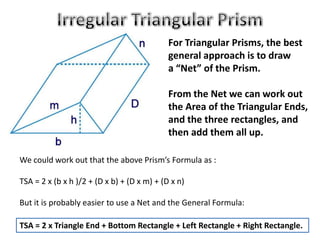
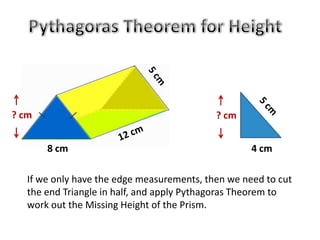
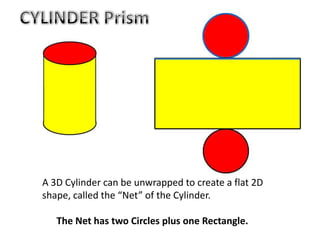
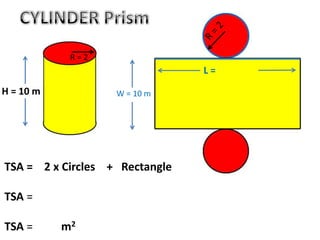
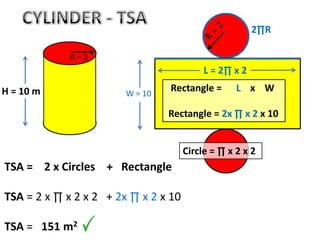
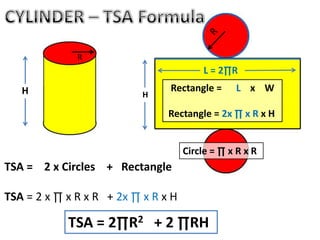
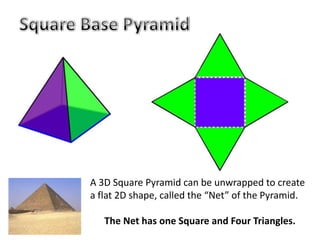
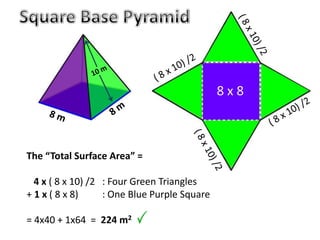
The document discusses calculating the total surface area (TSA) of different 3D shapes by unfolding them into their 2D nets. It provides the TSA formulas and worked examples for rectangular prisms, triangular prisms, cylinders, and square pyramids. Engineers, builders and others use TSA to determine material needs like paint or carpet for projects. The document emphasizes that TSA is an area measurement, not a volume.

1. Image Source: http://www.pbs.org

2. Image Source: http://www.ppfl.org
Total Surface Area is important for Painters,
so that they know how much paint will be required for a job.
Engineers, Designers, Scientists, Builders, Concreters,
Carpet Layers, and others also use Total Surface Areas
as part of their work.

3. A 3D Rectangular Prism
can be unfolded to create
a flat 2D shape, called the
“Net” of the Prism.

4. The “Total Surface Area” or
“TSA” of the Prism is the
Area of all of the six faces
added together.
Each of the Faces is a L x W
Rectangle.
8 cm
4 cm

5. The “Total Surface Area” =
2 x ( 8 x 5) : Two Blues
+ 2 x ( 8 x 4) : Two Yellows
+ 2 x ( 4 x 5) : Two Reds
= 2x40 + 2x32 + 2x20
= 184 cm2
8 cm
4 cm
8 x 5 8 x 5
4 x 5
4 x 5
8 x 4 8 x 4

6. The “Total Surface Area” =
2 x ( L x W ) : Two Blues
+ 2 x ( L x H ) : Two Yellows
+ 2 x ( W x H ) : Two Reds
L
H
L x W L x W
W x H
W x H
L x H L x H
TSA = 2 x(L x W) + 2x(L x H) + 2x(W x H)

7. TSA = 2 x ( x ) + 2 x ( x ) + 2 x ( x )
TSA = + +
TSA =
TSA = 2 x(L x W) + 2x(L x H) + 2x(W x H)
6 m
3 m
We can do the TSA of a
Rectangular Prism without
drawing out the flat 2D net.
All we do is apply the Formula.

8. TSA = 2 x ( 6 x 4 ) + 2 x ( 6 x 3 ) + 2 x ( 4 x 3 )
TSA = 48 + 36 + 24
TSA = 108 m2 ( Note that units are AREA m2 and Not VOLUME m3 )
6 m
3 m
TSA = 2 x(L x W) + 2x(L x H) + 2x(W x H)
We can do the TSA of a
Rectangular Prism without
drawing out the flat 2D net.
All we do is apply the Formula.

9. The Toblerone chocolate bar packaging is a
classic example of a Triangular Prism.
Image Source: http://www.blogspot.com

10. A 3D Triangular Prism
can be unfolded to create
a flat 2D shape, called the
“Net” of the Prism.
The Net has two triangles
plus three rectangles.

11. The “Total Surface Area” =
2 x ( 6 x 5) /2 : Two Reds
+ 2 x ( 8 x 7) : Two Yellows
+ 1 x ( 8 x 6) : One Green
= 2x15 + 2x56 + 1x48
= 190 mm2
6 mm
5 mm
8 x 7
( 6 x 5) /2
8 x 6 8 x 7
( 6 x 5) /2

12. The “Total Surface Area” =
2 x ( b x h) /2 : Two Reds
+ 2 x ( D x n) : Two Yellows
+ 1 x ( D x b) : One Green
Base b
Height h
D x n
( b x h) /2
D x b D x n
( b x h) /2TSA = 2 x (b x h)/2 + 2 x (D x n) + (D x b)
Only Works for Isosceles Triangle Ended Prisms
Only Works for Isosceles Triangle Ends

13. For Triangular Prisms, the best
general approach is to draw
a “Net” of the Prism.
From the Net we can work out
the Area of the Triangular Ends,
and the three rectangles, and
then add them all up.
We could work out that the above Prism’s Formula as :
TSA = 2 x (b x h )/2 + (D x b) + (D x m) + (D x n)
But it is probably easier to use a Net and the General Formula:
TSA = 2 x Triangle End + Bottom Rectangle + Left Rectangle + Right Rectangle.

14. If we only have the edge measurements, then we need to cut
the end Triangle in half, and apply Pythagoras Theorem to
work out the Missing Height of the Prism.
4 cm
? cm ? cm
8 cm

15. A 3D Cylinder can be unwrapped to create a flat 2D
shape, called the “Net” of the Cylinder.
The Net has two Circles plus one Rectangle.

16. W = 10 mH = 10 m
TSA = 2 x Circles + Rectangle
TSA =
TSA = m2
R = 2
L =

17. TSA = 2 x Circles + Rectangle
TSA = 2 x ∏ x 2 x 2 + 2x ∏ x 2 x 10
TSA = 151 m2
W = 10
2∏R
L = 2∏ x 2
Rectangle = L x W
Rectangle = 2x ∏ x 2 x 10
Circle = ∏ x 2 x 2
H = 10 m
R = 2

18. TSA = 2 x Circles + Rectangle
TSA = 2 x ∏ x R x R + 2x ∏ x R x H
H
L = 2∏R
Rectangle = L x W
Rectangle = 2x ∏ x R x H
Circle = ∏ x R x R
H
TSA = 2∏R2 + 2 ∏RH
R

19. TSA = 2 x ∏ x R x R + 2 x ∏ x R x H
TSA = 2 x 3.1416 x 3 x 3 + 2 x 3.1416 x 3 x 8
TSA = 207.3 m2
H = 8 m
TSA = 2∏R2 + 2 ∏RH
R = 3 m
We can do the TSA of a
Cylinder without having to
draw out the flat 2D net.
All we do is apply the TSA Formula.

20. A 3D Square Pyramid can be unwrapped to create
a flat 2D shape, called the “Net” of the Pyramid.
The Net has one Square and Four Triangles.

21. The “Total Surface Area” =
4 x ( 8 x 10) /2 : Four Green Triangles
+ 1 x ( 8 x 8) : One Blue Purple Square
= 4x40 + 1x64 = 224 m2
8 x 8

22. http://passyworldofmathematics.com/
All slides are exclusive Copyright of Passy’s World of Mathematics
Visit our site for Free Mathematics PowerPoints