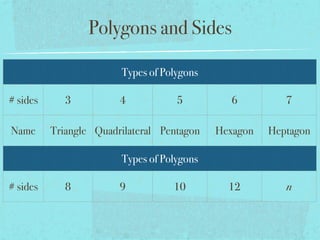
The document summarizes key concepts about polygons, including: - The sum of the interior angles of a polygon with n sides is (n-2)180 degrees. - The sum of the exterior angles of a polygon is 360 degrees. - Examples are provided to demonstrate calculating sums of interior/exterior angles and finding missing angle measures using angle sums. - Regular polygons are defined by their number of sides.

1. Chapter 6
Quadrilaterals
Created at wordle.net

2. Section 6-1
Angles of Polygons

3. Essential Questions
How do you find and use the sum of the measures of the interior
angles of a polygon?
How do you find and use the sum of the measures of the exterior
angles of a polygon?

4. Vocabulary
1. Diagonal:

5. Vocabulary
1. Diagonal: A segment in a polygon that connects a vertex with
another vertex that is nonconsecutive

6. Theorems
6.1 - Polygon Interior Angles Sum:
6.2 - Polygon Exterior Angles Sum:

7. Theorems
6.1 - Polygon Interior Angles Sum: The sum of the interior angle
measures of a convex polygon with n sides is found with the formula
S =(n−2)180
6.2 - Polygon Exterior Angles Sum:

8. Theorems
6.1 - Polygon Interior Angles Sum: The sum of the interior angle
measures of a convex polygon with n sides is found with the formula
S =(n−2)180
6.2 - Polygon Exterior Angles Sum: The sum of the exterior angle
measures of a convex polygon, one at each vertex, is 360°

9. Polygons and Sides

10. Polygons and Sides
Types of Polygons

11. Polygons and Sides
Types of Polygons
# sides 3 4 5 6 7

12. Polygons and Sides
Types of Polygons
# sides 3 4 5 6 7
Name Triangle Quadrilateral Pentagon Hexagon Heptagon

13. Polygons and Sides
Types of Polygons
# sides 3 4 5 6 7
Name Triangle Quadrilateral Pentagon Hexagon Heptagon
Types of Polygons

14. Polygons and Sides
Types of Polygons
# sides 3 4 5 6 7
Name Triangle Quadrilateral Pentagon Hexagon Heptagon
Types of Polygons
# sides 8 9 10 12 n

15. Polygons and Sides
Types of Polygons
# sides 3 4 5 6 7
Name Triangle Quadrilateral Pentagon Hexagon Heptagon
Types of Polygons
# sides 8 9 10 12 n
Name Octagon Nonagon Decagon Dodecagon n-gon

16. Example 1
Find the sum of the measures of the interior angles of the following.
a. Nonagon b. 17-gon

17. Example 1
Find the sum of the measures of the interior angles of the following.
a. Nonagon b. 17-gon
S =(n−2)180

18. Example 1
Find the sum of the measures of the interior angles of the following.
a. Nonagon b. 17-gon
S =(n−2)180
S =(9−2)180

19. Example 1
Find the sum of the measures of the interior angles of the following.
a. Nonagon b. 17-gon
S =(n−2)180
S =(9−2)180
=(7)180

20. Example 1
Find the sum of the measures of the interior angles of the following.
a. Nonagon b. 17-gon
S =(n−2)180
S =(9−2)180
=(7)180
=1260°

21. Example 1
Find the sum of the measures of the interior angles of the following.
a. Nonagon b. 17-gon
S =(n−2)180
S =(9−2)180
=(7)180
=1260°
S =(n−2)180

22. Example 1
Find the sum of the measures of the interior angles of the following.
a. Nonagon b. 17-gon
S =(n−2)180
S =(9−2)180
=(7)180
=1260°
S =(n−2)180
S =(17−2)180

23. Example 1
Find the sum of the measures of the interior angles of the following.
a. Nonagon b. 17-gon
S =(n−2)180
S =(9−2)180
=(7)180
=1260°
S =(n−2)180
S =(17−2)180
=(15)180

24. Example 1
Find the sum of the measures of the interior angles of the following.
a. Nonagon b. 17-gon
S =(n−2)180
S =(9−2)180
=(7)180
=1260°
S =(n−2)180
S =(17−2)180
=(15)180
=2700°

25. Example 2
Find the measure of each interior angle of parallelogram RSTU.

26. Example 2
Find the measure of each interior angle of parallelogram RSTU.
S =(n−2)180

27. Example 2
Find the measure of each interior angle of parallelogram RSTU.
S =(n−2)180
S =(4−2)180

28. Example 2
Find the measure of each interior angle of parallelogram RSTU.
S =(n−2)180
S =(4−2)180
=(2)180

29. Example 2
Find the measure of each interior angle of parallelogram RSTU.
S =(n−2)180
S =(4−2)180
=(2)180
=360°

30. Example 2
Find the measure of each interior angle of parallelogram RSTU.
S =(n−2)180
S =(4−2)180
=(2)180
=360°
11x +4+5x +11x +4+5x =360

31. Example 2
Find the measure of each interior angle of parallelogram RSTU.
S =(n−2)180
S =(4−2)180
=(2)180
=360°
11x +4+5x +11x +4+5x =360
32x +8=360

32. Example 2
Find the measure of each interior angle of parallelogram RSTU.
S =(n−2)180
S =(4−2)180
=(2)180
=360°
11x +4+5x +11x +4+5x =360
32x +8=360
−8 −8

33. Example 2
Find the measure of each interior angle of parallelogram RSTU.
S =(n−2)180
S =(4−2)180
=(2)180
=360°
11x +4+5x +11x +4+5x =360
32x +8=360
−8 −8
32x =352

34. Example 2
Find the measure of each interior angle of parallelogram RSTU.
S =(n−2)180
S =(4−2)180
=(2)180
=360°
11x +4+5x +11x +4+5x =360
32x +8=360
−8 −8
32x =352
32 32

35. Example 2
Find the measure of each interior angle of parallelogram RSTU.
S =(n−2)180
S =(4−2)180
=(2)180
=360°
11x +4+5x +11x +4+5x =360
32x +8=360
−8 −8
32x =352
32 32
x =11

36. Example 2
Find the measure of each interior angle of parallelogram RSTU.
S =(n−2)180
S =(4−2)180
=(2)180
=360°
11x +4+5x +11x +4+5x =360
32x +8=360
−8 −8
32x =352
32 32
x =11
m∠R = m∠T =5(11)

37. Example 2
Find the measure of each interior angle of parallelogram RSTU.
S =(n−2)180
S =(4−2)180
=(2)180
=360°
11x +4+5x +11x +4+5x =360
32x +8=360
−8 −8
32x =352
32 32
x =11
m∠R = m∠T =5(11) =55°

38. Example 2
Find the measure of each interior angle of parallelogram RSTU.
S =(n−2)180
S =(4−2)180
=(2)180
=360°
11x +4+5x +11x +4+5x =360
32x +8=360
−8 −8
32x =352
32 32
x =11
m∠R = m∠T =5(11) =55°
m∠S = m∠U =11(11)+4

39. Example 2
Find the measure of each interior angle of parallelogram RSTU.
S =(n−2)180
S =(4−2)180
=(2)180
=360°
11x +4+5x +11x +4+5x =360
32x +8=360
−8 −8
32x =352
32 32
x =11
m∠R = m∠T =5(11) =55°
m∠S = m∠U =11(11)+4
=121+4

40. Example 2
Find the measure of each interior angle of parallelogram RSTU.
S =(n−2)180
S =(4−2)180
=(2)180
=360°
11x +4+5x +11x +4+5x =360
32x +8=360
−8 −8
32x =352
32 32
x =11
m∠R = m∠T =5(11) =55°
m∠S = m∠U =11(11)+4
=121+4 =125°

41. Example 3
Park City Mall is designed so that eight walkways meet in a central area in
the shape of a regular octagon. Find the measure of one of the interior
angles of the octagon.
http://www.parkcitycenter.com/directory

42. Example 3
Park City Mall is designed so that eight walkways meet in a central area in
the shape of a regular octagon. Find the measure of one of the interior
angles of the octagon.
S =(n−2)180
http://www.parkcitycenter.com/directory

43. Example 3
Park City Mall is designed so that eight walkways meet in a central area in
the shape of a regular octagon. Find the measure of one of the interior
angles of the octagon.
S =(n−2)180
S =(8−2)180
http://www.parkcitycenter.com/directory

44. Example 3
Park City Mall is designed so that eight walkways meet in a central area in
the shape of a regular octagon. Find the measure of one of the interior
angles of the octagon.
S =(n−2)180
S =(8−2)180
=(6)180
http://www.parkcitycenter.com/directory

45. Example 3
Park City Mall is designed so that eight walkways meet in a central area in
the shape of a regular octagon. Find the measure of one of the interior
angles of the octagon.
S =(n−2)180
S =(8−2)180
=(6)180
=1080° http://www.parkcitycenter.com/directory

46. Example 3
Park City Mall is designed so that eight walkways meet in a central area in
the shape of a regular octagon. Find the measure of one of the interior
angles of the octagon.
S =(n−2)180
S =(8−2)180
=(6)180
=1080°
1080°
8 http://www.parkcitycenter.com/directory

47. Example 3
Park City Mall is designed so that eight walkways meet in a central area in
the shape of a regular octagon. Find the measure of one of the interior
angles of the octagon.
S =(n−2)180
S =(8−2)180
=(6)180
=1080°
1080°
8
=135° http://www.parkcitycenter.com/directory

48. Example 4
The measure of an interior angle of a regular polygon is 150°. Find the
number of sides in the polygon.

49. Example 4
The measure of an interior angle of a regular polygon is 150°. Find the
number of sides in the polygon.
150n=(n−2)180

50. Example 4
The measure of an interior angle of a regular polygon is 150°. Find the
number of sides in the polygon.
150n=(n−2)180
150n=180n−360

51. Example 4
The measure of an interior angle of a regular polygon is 150°. Find the
number of sides in the polygon.
150n=(n−2)180
150n=180n−360
−180n −180n

52. Example 4
The measure of an interior angle of a regular polygon is 150°. Find the
number of sides in the polygon.
150n=(n−2)180
150n=180n−360
−180n −180n
−30n= −360

53. Example 4
The measure of an interior angle of a regular polygon is 150°. Find the
number of sides in the polygon.
150n=(n−2)180
150n=180n−360
−180n −180n
−30n= −360
−30 −30

54. Example 4
The measure of an interior angle of a regular polygon is 150°. Find the
number of sides in the polygon.
150n=(n−2)180
150n=180n−360
−180n −180n
−30n= −360
−30 −30
n=12

55. Example 4
The measure of an interior angle of a regular polygon is 150°. Find the
number of sides in the polygon.
150n=(n−2)180
150n=180n−360
−180n −180n
−30n= −360
−30 −30
n=12
There are 12 sides to the polygon

56. Example 5
Find the value of x in the diagram.
m∠1=5x +5, m∠2=5x, m∠3= 4x −6,
m∠4=5x −5, m∠5= 4x +3, m∠6=6x −12,
m∠7=2x +3

57. Example 5
Find the value of x in the diagram.
m∠1=5x +5, m∠2=5x, m∠3= 4x −6,
m∠4=5x −5, m∠5= 4x +3, m∠6=6x −12,
m∠7=2x +3
5x +5+5x +4x −6+5x −5+4x +3+6x −12+2x +3=360

58. Example 5
Find the value of x in the diagram.
m∠1=5x +5, m∠2=5x, m∠3= 4x −6,
m∠4=5x −5, m∠5= 4x +3, m∠6=6x −12,
m∠7=2x +3
5x +5+5x +4x −6+5x −5+4x +3+6x −12+2x +3=360
31x −12=360

59. Example 5
Find the value of x in the diagram.
m∠1=5x +5, m∠2=5x, m∠3= 4x −6,
m∠4=5x −5, m∠5= 4x +3, m∠6=6x −12,
m∠7=2x +3
5x +5+5x +4x −6+5x −5+4x +3+6x −12+2x +3=360
31x −12=360
31x =372

60. Example 5
Find the value of x in the diagram.
m∠1=5x +5, m∠2=5x, m∠3= 4x −6,
m∠4=5x −5, m∠5= 4x +3, m∠6=6x −12,
m∠7=2x +3
5x +5+5x +4x −6+5x −5+4x +3+6x −12+2x +3=360
31x −12=360
31x =372
x =12