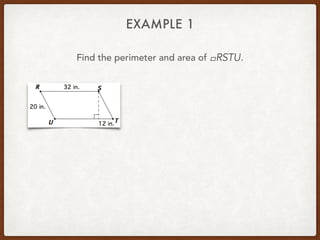
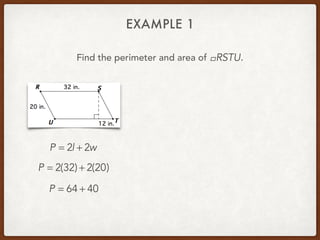
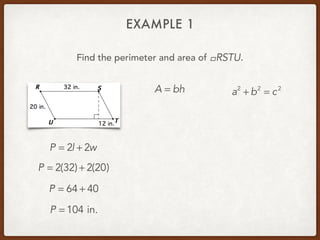
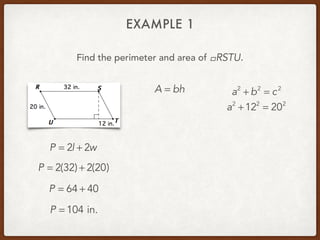
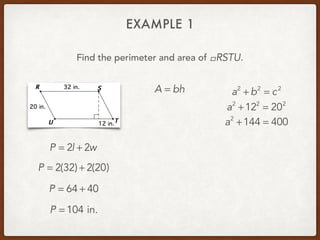
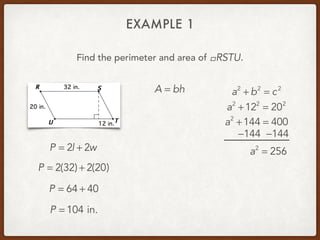
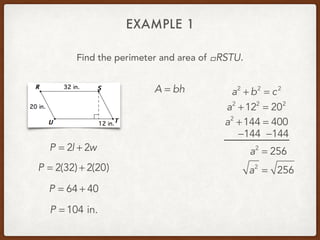
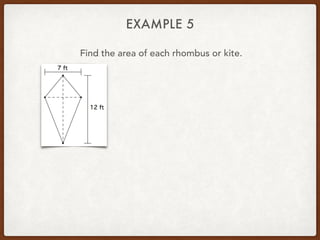
The document discusses finding areas and perimeters of various shapes such as parallelograms, triangles, trapezoids, and rhombi. It provides definitions for key terms used to calculate these measurements, such as base and height. Several examples are shown calculating perimeters and areas of specific shapes by applying the appropriate formulas. Methods for finding missing values like side lengths using properties of shapes are demonstrated.

1. EXTENDING AREA, SURFACE AREA, AND
VOLUME
CHAPTER 11/12

2. AREAS OF PARALLELOGRAMS,
TRIANGLES, RHOMBI, AND
TRAPEZOIDS
SECTION 11-1 AND 11-2

3. ESSENTIAL QUESTIONS
• How do you find perimeters and areas of
parallelograms?
• How do you find perimeters and areas of
triangles?
• How do you find areas of trapezoids?
• How do you find areas of rhombi and kites?

4. VOCABULARY
1. Base of a Parallelogram:
2. Height of a Parallelogram:
3. Base of a Triangle:
4. Height of a Triangle:
5. Height of a Trapezoid:

5. VOCABULARY
1. Base of a Parallelogram:
2. Height of a Parallelogram:
3. Base of a Triangle:
4. Height of a Triangle:
5. Height of a Trapezoid:
Can be any side of a parallelogram

6. VOCABULARY
1. Base of a Parallelogram:
2. Height of a Parallelogram:
3. Base of a Triangle:
4. Height of a Triangle:
5. Height of a Trapezoid:
Can be any side of a parallelogram
The perpendicular distance between
any two parallel bases of a parallelogram

7. VOCABULARY
1. Base of a Parallelogram:
2. Height of a Parallelogram:
3. Base of a Triangle:
4. Height of a Triangle:
5. Height of a Trapezoid:
Can be any side of a parallelogram
The perpendicular distance between
any two parallel bases of a parallelogram
Can be any side of a triangle

8. VOCABULARY
1. Base of a Parallelogram:
2. Height of a Parallelogram:
3. Base of a Triangle:
4. Height of a Triangle:
5. Height of a Trapezoid:
Can be any side of a parallelogram
The perpendicular distance between
any two parallel bases of a parallelogram
Can be any side of a triangle
The length of a segment perpendicular to a
base to the opposite vertex

9. VOCABULARY
1. Base of a Parallelogram:
2. Height of a Parallelogram:
3. Base of a Triangle:
4. Height of a Triangle:
5. Height of a Trapezoid:
Can be any side of a parallelogram
The perpendicular distance between
any two parallel bases of a parallelogram
Can be any side of a triangle
The length of a segment perpendicular to a
base to the opposite vertex
The perpendicular distance between bases

10. EXAMPLE 1
Find the perimeter and area of .!RSTU

11. EXAMPLE 1
Find the perimeter and area of .!RSTU
P = 2l + 2w

12. EXAMPLE 1
Find the perimeter and area of .!RSTU
P = 2l + 2w
P = 2(32) + 2(20)

13. EXAMPLE 1
Find the perimeter and area of .!RSTU
P = 2l + 2w
P = 2(32) + 2(20)
P = 64 + 40

14. EXAMPLE 1
Find the perimeter and area of .!RSTU
P = 2l + 2w
P = 2(32) + 2(20)
P = 64 + 40
P = 104 in.

15. EXAMPLE 1
Find the perimeter and area of .!RSTU
P = 2l + 2w
P = 2(32) + 2(20)
P = 64 + 40
P = 104 in.
A = bh

16. EXAMPLE 1
Find the perimeter and area of .!RSTU
P = 2l + 2w
P = 2(32) + 2(20)
P = 64 + 40
P = 104 in.
A = bh a2
+ b2
= c2

17. EXAMPLE 1
Find the perimeter and area of .!RSTU
P = 2l + 2w
P = 2(32) + 2(20)
P = 64 + 40
P = 104 in.
A = bh a2
+ b2
= c2
a2
+122
= 202

18. EXAMPLE 1
Find the perimeter and area of .!RSTU
P = 2l + 2w
P = 2(32) + 2(20)
P = 64 + 40
P = 104 in.
A = bh a2
+ b2
= c2
a2
+122
= 202
a2
+144 = 400

19. EXAMPLE 1
Find the perimeter and area of .!RSTU
P = 2l + 2w
P = 2(32) + 2(20)
P = 64 + 40
P = 104 in.
A = bh a2
+ b2
= c2
a2
+122
= 202
a2
+144 = 400
−144 −144

20. EXAMPLE 1
Find the perimeter and area of .!RSTU
P = 2l + 2w
P = 2(32) + 2(20)
P = 64 + 40
P = 104 in.
A = bh a2
+ b2
= c2
a2
+122
= 202
a2
+144 = 400
−144 −144
a2
= 256

21. EXAMPLE 1
Find the perimeter and area of .!RSTU
P = 2l + 2w
P = 2(32) + 2(20)
P = 64 + 40
P = 104 in.
A = bh a2
+ b2
= c2
a2
+122
= 202
a2
+144 = 400
−144 −144
a2
= 256
a2
= 256

22. EXAMPLE 1
Find the perimeter and area of .!RSTU
P = 2l + 2w
P = 2(32) + 2(20)
P = 64 + 40
P = 104 in.
A = bh a2
+ b2
= c2
a2
+122
= 202
a2
+144 = 400
−144 −144
a2
= 256
a2
= 256
a = 16

23. EXAMPLE 1
Find the perimeter and area of .!RSTU
P = 2l + 2w
P = 2(32) + 2(20)
P = 64 + 40
P = 104 in.
A = bh a2
+ b2
= c2
a2
+122
= 202
a2
+144 = 400
−144 −144
a2
= 256
a2
= 256
a = 16
h = 16

24. EXAMPLE 1
Find the perimeter and area of .!RSTU
P = 2l + 2w
P = 2(32) + 2(20)
P = 64 + 40
P = 104 in.
A = bh a2
+ b2
= c2
a2
+122
= 202
a2
+144 = 400
−144 −144
a2
= 256
a2
= 256
a = 16
h = 16
A = 32(16)

25. EXAMPLE 1
Find the perimeter and area of .!RSTU
P = 2l + 2w
P = 2(32) + 2(20)
P = 64 + 40
P = 104 in.
A = bh a2
+ b2
= c2
a2
+122
= 202
a2
+144 = 400
−144 −144
a2
= 256
a2
= 256
a = 16
h = 16
A = 32(16)
A = 512 in2

26. EXAMPLE 2
Matt Mitarnowski needs to buy enough boards to make the frame
of the triangular sandbox shown and enough sand to cover the
bottom. If one of the boards is 3 feet long and one bag of sand
covers 9 square feet of the sandbox, how many boards and bags
does he need to buy?

27. EXAMPLE 2
Matt Mitarnowski needs to buy enough boards to make the frame
of the triangular sandbox shown and enough sand to cover the
bottom. If one of the boards is 3 feet long and one bag of sand
covers 9 square feet of the sandbox, how many boards and bags
does he need to buy?
P = a + b + c

28. EXAMPLE 2
Matt Mitarnowski needs to buy enough boards to make the frame
of the triangular sandbox shown and enough sand to cover the
bottom. If one of the boards is 3 feet long and one bag of sand
covers 9 square feet of the sandbox, how many boards and bags
does he need to buy?
P = a + b + c
P = 12+16 + 7.5

29. EXAMPLE 2
Matt Mitarnowski needs to buy enough boards to make the frame
of the triangular sandbox shown and enough sand to cover the
bottom. If one of the boards is 3 feet long and one bag of sand
covers 9 square feet of the sandbox, how many boards and bags
does he need to buy?
P = a + b + c
P = 12+16 + 7.5
P = 35.5 ft

30. EXAMPLE 2
Matt Mitarnowski needs to buy enough boards to make the frame
of the triangular sandbox shown and enough sand to cover the
bottom. If one of the boards is 3 feet long and one bag of sand
covers 9 square feet of the sandbox, how many boards and bags
does he need to buy?
P = a + b + c
P = 12+16 + 7.5
P = 35.5 ft
35.5
3

31. EXAMPLE 2
Matt Mitarnowski needs to buy enough boards to make the frame
of the triangular sandbox shown and enough sand to cover the
bottom. If one of the boards is 3 feet long and one bag of sand
covers 9 square feet of the sandbox, how many boards and bags
does he need to buy?
P = a + b + c
P = 12+16 + 7.5
P = 35.5 ft
35.5
3
≈ 11.83

32. EXAMPLE 2
Matt Mitarnowski needs to buy enough boards to make the frame
of the triangular sandbox shown and enough sand to cover the
bottom. If one of the boards is 3 feet long and one bag of sand
covers 9 square feet of the sandbox, how many boards and bags
does he need to buy?
P = a + b + c
P = 12+16 + 7.5
P = 35.5 ft
35.5
3
≈ 11.83 Matt needs 12 boards.

33. EXAMPLE 2
Matt Mitarnowski needs to buy enough boards to make the frame
of the triangular sandbox shown and enough sand to cover the
bottom. If one of the boards is 3 feet long and one bag of sand
covers 9 square feet of the sandbox, how many boards and bags
does he need to buy?
P = a + b + c
P = 12+16 + 7.5
P = 35.5 ft
35.5
3
≈ 11.83
A = 1
2
bh
Matt needs 12 boards.

34. EXAMPLE 2
Matt Mitarnowski needs to buy enough boards to make the frame
of the triangular sandbox shown and enough sand to cover the
bottom. If one of the boards is 3 feet long and one bag of sand
covers 9 square feet of the sandbox, how many boards and bags
does he need to buy?
P = a + b + c
P = 12+16 + 7.5
P = 35.5 ft
35.5
3
≈ 11.83
A = 1
2
bh
Matt needs 12 boards.
A = 1
2
(12)(9)

35. EXAMPLE 2
Matt Mitarnowski needs to buy enough boards to make the frame
of the triangular sandbox shown and enough sand to cover the
bottom. If one of the boards is 3 feet long and one bag of sand
covers 9 square feet of the sandbox, how many boards and bags
does he need to buy?
P = a + b + c
P = 12+16 + 7.5
P = 35.5 ft
35.5
3
≈ 11.83
A = 1
2
bh
Matt needs 12 boards.
A = 1
2
(12)(9)
A = 54 ft2

36. EXAMPLE 2
Matt Mitarnowski needs to buy enough boards to make the frame
of the triangular sandbox shown and enough sand to cover the
bottom. If one of the boards is 3 feet long and one bag of sand
covers 9 square feet of the sandbox, how many boards and bags
does he need to buy?
P = a + b + c
P = 12+16 + 7.5
P = 35.5 ft
35.5
3
≈ 11.83
A = 1
2
bh
Matt needs 12 boards.
A = 1
2
(12)(9)
A = 54 ft2
54
9

37. EXAMPLE 2
Matt Mitarnowski needs to buy enough boards to make the frame
of the triangular sandbox shown and enough sand to cover the
bottom. If one of the boards is 3 feet long and one bag of sand
covers 9 square feet of the sandbox, how many boards and bags
does he need to buy?
P = a + b + c
P = 12+16 + 7.5
P = 35.5 ft
35.5
3
≈ 11.83
A = 1
2
bh
Matt needs 12 boards.
A = 1
2
(12)(9)
A = 54 ft2
54
9
= 6

38. EXAMPLE 2
Matt Mitarnowski needs to buy enough boards to make the frame
of the triangular sandbox shown and enough sand to cover the
bottom. If one of the boards is 3 feet long and one bag of sand
covers 9 square feet of the sandbox, how many boards and bags
does he need to buy?
P = a + b + c
P = 12+16 + 7.5
P = 35.5 ft
35.5
3
≈ 11.83
A = 1
2
bh
Matt needs 12 boards.
A = 1
2
(12)(9)
A = 54 ft2
54
9
= 6
Matt needs 6 bags of
sand.

39. POSTULATE 11.2
If two figures are congruent, then they have the same area.

40. EXAMPLE 3
Find the area of the trapezoid.

41. EXAMPLE 3
Find the area of the trapezoid.
A = 1
2
h(b1
+ b2
)

42. EXAMPLE 3
Find the area of the trapezoid.
A = 1
2
h(b1
+ b2
)
A = 1
2
(1)(3 + 2.5)

43. EXAMPLE 3
Find the area of the trapezoid.
A = 1
2
h(b1
+ b2
)
A = 1
2
(1)(3 + 2.5)
A = 1
2
(5.5)

44. EXAMPLE 3
Find the area of the trapezoid.
A = 1
2
h(b1
+ b2
)
A = 1
2
(1)(3 + 2.5)
A = 1
2
(5.5)
A = 2.75 cm2

45. EXAMPLE 4
Fuzzy Jeff designed a deck shaped like the trapezoid shown. Find
the area of the deck.

46. EXAMPLE 4
Fuzzy Jeff designed a deck shaped like the trapezoid shown. Find
the area of the deck.
a2
+ b2
= c2

47. EXAMPLE 4
Fuzzy Jeff designed a deck shaped like the trapezoid shown. Find
the area of the deck.
a2
+ b2
= c2
42
+ b2
= 52

48. EXAMPLE 4
Fuzzy Jeff designed a deck shaped like the trapezoid shown. Find
the area of the deck.
a2
+ b2
= c2
42
+ b2
= 52
16 + b2
= 25

49. EXAMPLE 4
Fuzzy Jeff designed a deck shaped like the trapezoid shown. Find
the area of the deck.
a2
+ b2
= c2
42
+ b2
= 52
16 + b2
= 25
−16 −16

50. EXAMPLE 4
Fuzzy Jeff designed a deck shaped like the trapezoid shown. Find
the area of the deck.
a2
+ b2
= c2
42
+ b2
= 52
16 + b2
= 25
−16 −16
b2
= 9

51. EXAMPLE 4
Fuzzy Jeff designed a deck shaped like the trapezoid shown. Find
the area of the deck.
a2
+ b2
= c2
42
+ b2
= 52
16 + b2
= 25
−16 −16
b2
= 9
b2
= 9

52. EXAMPLE 4
Fuzzy Jeff designed a deck shaped like the trapezoid shown. Find
the area of the deck.
a2
+ b2
= c2
42
+ b2
= 52
16 + b2
= 25
−16 −16
b2
= 9
b2
= 9 b = 3

53. EXAMPLE 4
Fuzzy Jeff designed a deck shaped like the trapezoid shown. Find
the area of the deck.
a2
+ b2
= c2
42
+ b2
= 52
16 + b2
= 25
−16 −16
b2
= 9
b2
= 9 b = 3
b1
= 9; b2
= 9 − 3 = 6

54. EXAMPLE 4
Fuzzy Jeff designed a deck shaped like the trapezoid shown. Find
the area of the deck.
a2
+ b2
= c2
42
+ b2
= 52
16 + b2
= 25
−16 −16
b2
= 9
b2
= 9 b = 3
b1
= 9; b2
= 9 − 3 = 6
A = 1
2
h(b1
+ b2
)

55. EXAMPLE 4
Fuzzy Jeff designed a deck shaped like the trapezoid shown. Find
the area of the deck.
a2
+ b2
= c2
42
+ b2
= 52
16 + b2
= 25
−16 −16
b2
= 9
b2
= 9 b = 3
b1
= 9; b2
= 9 − 3 = 6
A = 1
2
h(b1
+ b2
)
A = 1
2
(4)(6 + 9)

56. EXAMPLE 4
Fuzzy Jeff designed a deck shaped like the trapezoid shown. Find
the area of the deck.
a2
+ b2
= c2
42
+ b2
= 52
16 + b2
= 25
−16 −16
b2
= 9
b2
= 9 b = 3
b1
= 9; b2
= 9 − 3 = 6
A = 1
2
h(b1
+ b2
)
A = 1
2
(4)(6 + 9)
A = (2)(15)

57. EXAMPLE 4
Fuzzy Jeff designed a deck shaped like the trapezoid shown. Find
the area of the deck.
a2
+ b2
= c2
42
+ b2
= 52
16 + b2
= 25
−16 −16
b2
= 9
b2
= 9 b = 3
b1
= 9; b2
= 9 − 3 = 6
A = 1
2
h(b1
+ b2
)
A = 1
2
(4)(6 + 9)
A = (2)(15)
A = 30 ft2

58. EXAMPLE 5
Find the area of each rhombus or kite.

59. EXAMPLE 5
Find the area of each rhombus or kite.
A = 1
2
d1
d2

60. EXAMPLE 5
Find the area of each rhombus or kite.
A = 1
2
d1
d2
A = 1
2
(7)(12)

61. EXAMPLE 5
Find the area of each rhombus or kite.
A = 1
2
d1
d2
A = 1
2
(7)(12)
A = 42 ft2

62. EXAMPLE 5
Find the area of each rhombus or kite.

63. EXAMPLE 5
Find the area of each rhombus or kite.
A = 1
2
d1
d2

64. EXAMPLE 5
Find the area of each rhombus or kite.
A = 1
2
d1
d2
A = 1
2
(14)(18)

65. EXAMPLE 5
Find the area of each rhombus or kite.
A = 1
2
d1
d2
A = 1
2
(14)(18)
A = 126 in2

66. EXAMPLE 6
One diagonal of a rhombus is half as long as the other diagonal. If
the area of the rhombus is 64 square inches, what are the lengths
of the diagonals?

67. EXAMPLE 6
One diagonal of a rhombus is half as long as the other diagonal. If
the area of the rhombus is 64 square inches, what are the lengths
of the diagonals?
A = 1
2
d1
d2

68. EXAMPLE 6
One diagonal of a rhombus is half as long as the other diagonal. If
the area of the rhombus is 64 square inches, what are the lengths
of the diagonals?
A = 1
2
d1
d2
d1
= x

69. EXAMPLE 6
One diagonal of a rhombus is half as long as the other diagonal. If
the area of the rhombus is 64 square inches, what are the lengths
of the diagonals?
A = 1
2
d1
d2
d1
= x
d2
= 1
2
x

70. EXAMPLE 6
One diagonal of a rhombus is half as long as the other diagonal. If
the area of the rhombus is 64 square inches, what are the lengths
of the diagonals?
A = 1
2
d1
d2
d1
= x
d2
= 1
2
x
64 = 1
2
(x)(1
2
x)

71. EXAMPLE 6
One diagonal of a rhombus is half as long as the other diagonal. If
the area of the rhombus is 64 square inches, what are the lengths
of the diagonals?
A = 1
2
d1
d2
d1
= x
d2
= 1
2
x
64 = 1
2
(x)(1
2
x)
64 = 1
4
x2

72. EXAMPLE 6
One diagonal of a rhombus is half as long as the other diagonal. If
the area of the rhombus is 64 square inches, what are the lengths
of the diagonals?
A = 1
2
d1
d2
d1
= x
d2
= 1
2
x
64 = 1
2
(x)(1
2
x)
64 = 1
4
x2
4(64) = ( 1
4
x2
)4

73. EXAMPLE 6
One diagonal of a rhombus is half as long as the other diagonal. If
the area of the rhombus is 64 square inches, what are the lengths
of the diagonals?
A = 1
2
d1
d2
d1
= x
d2
= 1
2
x
64 = 1
2
(x)(1
2
x)
64 = 1
4
x2
4(64) = ( 1
4
x2
)4
256 = x2

74. EXAMPLE 6
One diagonal of a rhombus is half as long as the other diagonal. If
the area of the rhombus is 64 square inches, what are the lengths
of the diagonals?
A = 1
2
d1
d2
d1
= x
d2
= 1
2
x
64 = 1
2
(x)(1
2
x)
64 = 1
4
x2
4(64) = ( 1
4
x2
)4
256 = x2
256 = x2

75. EXAMPLE 6
One diagonal of a rhombus is half as long as the other diagonal. If
the area of the rhombus is 64 square inches, what are the lengths
of the diagonals?
A = 1
2
d1
d2
d1
= x
d2
= 1
2
x
64 = 1
2
(x)(1
2
x)
64 = 1
4
x2
4(64) = ( 1
4
x2
)4
256 = x2
256 = x2
x = 16

76. EXAMPLE 6
One diagonal of a rhombus is half as long as the other diagonal. If
the area of the rhombus is 64 square inches, what are the lengths
of the diagonals?
A = 1
2
d1
d2
d1
= x
d2
= 1
2
x
64 = 1
2
(x)(1
2
x)
64 = 1
4
x2
4(64) = ( 1
4
x2
)4
256 = x2
256 = x2
x = 16
d1
= 16 in.

77. EXAMPLE 6
One diagonal of a rhombus is half as long as the other diagonal. If
the area of the rhombus is 64 square inches, what are the lengths
of the diagonals?
A = 1
2
d1
d2
d1
= x
d2
= 1
2
x
64 = 1
2
(x)(1
2
x)
64 = 1
4
x2
4(64) = ( 1
4
x2
)4
256 = x2
256 = x2
x = 16
d1
= 16 in.
d2
= 8 in.

78. PROBLEM SET

79. PROBLEM SET
p. 767 #1, 2, 5-9 all; p. 777 #1-13 odd
“The best preparation for tomorrow is doing your best today.”
- H. Jackson Brown, Jr.