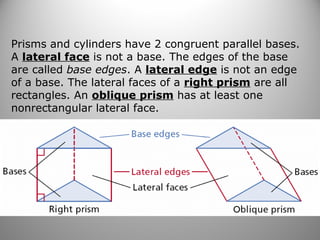
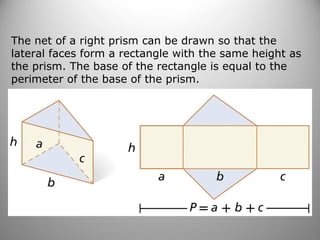
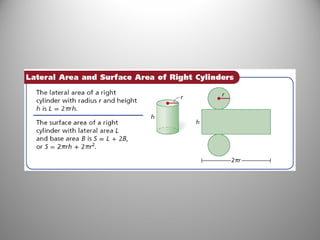
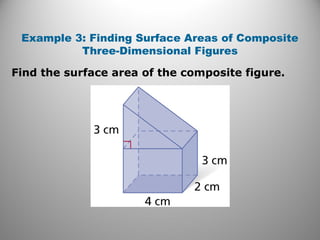
This document provides instruction on calculating the surface areas of prisms and cylinders. It defines key terms like lateral face, altitude, and axis. It presents formulas for calculating the surface area of right rectangular prisms and right cylinders. Examples are provided to demonstrate calculating surface areas of various prisms and cylinders. The document also addresses how surface areas change with modifications to dimensions and provides a word problem comparing the surface areas of different shapes.

1. UUNNIITT 1111..22 SSUURRFFAACCEE AARREEAASS OOFF
PPRRIISSMMSS AANNDD CCYYLLIINNDDEERRSS

2. Warm Up
Find the perimeter and area of
each polygon.
1. a rectangle with base 14 cm and height
9 cm
2. a right triangle with 9 cm and 12 cm
legs
3. an equilateral triangle with side length
6 cm
P = 46 cm; A = 126 cm2
P = 36 cm; A = 54 cm2

3. Objectives
Learn and apply the formula for the
surface area of a prism.
Learn and apply the formula for the
surface area of a cylinder.

4. lateral face
lateral edge
right prism
oblique prism
altitude
surface area
lateral surface
axis of a cylinder
right cylinder
oblique cylinder
Vocabulary

5. Prisms and cylinders have 2 congruent parallel bases.
A lateral face is not a base. The edges of the base
are called base edges. A lateral edge is not an edge
of a base. The lateral faces of a right prism are all
rectangles. An oblique prism has at least one
nonrectangular lateral face.

6. An altitude of a prism or cylinder is a perpendicular
segment joining the planes of the bases. The height of
a three-dimensional figure is the length of an altitude.
Surface area is the total area of all faces and curved
surfaces of a three-dimensional figure. The lateral
area of a prism is the sum of the areas of the lateral
faces.

7. The net of a right prism can be drawn so that the
lateral faces form a rectangle with the same height as
the prism. The base of the rectangle is equal to the
perimeter of the base of the prism.

8. The surface area of a right rectangular prism with
length ℓ, width w, and height h can be written as
S = 2ℓw + 2wh + 2ℓh.

9. Caution!
The surface area formula is only true for right
prisms. To find the surface area of an oblique
prism, add the areas of the faces.

10. Example 1A: Finding Lateral Areas and Surface Areas
of Prisms
Find the lateral area and surface area of the
right rectangular prism. Round to the nearest
tenth, if necessary.
L = Ph
= 32(14) = 448 ft2
S = Ph + 2B
= 448 + 2(7)(9) = 574 ft2
P = 2(9) + 2(7) = 32 ft

11. Example 1B: Finding Lateral Areas and Surface Areas
of Prisms
Find the lateral area and surface area of a right
regular triangular prism with height 20 cm and
base edges of length 10 cm. Round to the
nearest tenth, if necessary.
L = Ph
= 30(20) = 600 ft2
S = Ph + 2B
P = 3(10) = 30 cm
The base area is

12. Check It Out! Example 1
Find the lateral area and surface area of a cube
with edge length 8 cm.
L = Ph
= 32(8) = 256 cm2
S = Ph + 2B
= 256 + 2(8)(8) = 384 cm2
P = 4(8) = 32 cm

13. The lateral surface of a cylinder is the curved surface
that connects the two bases. The axis of a cylinder is
the segment with endpoints at the centers of the
bases. The axis of a right cylinder is perpendicular to
its bases. The axis of an oblique cylinder is not
perpendicular to its bases. The altitude of a right
cylinder is the same length as the axis.

15. Example 2A: Finding Lateral Areas and Surface Areas
of Right Cylinders
Find the lateral area and surface area of the
right cylinder. Give your answers in terms of p .
The radius is half the diameter,
or 8 ft.
L = 2prh = 2p(8)(10) = 160p in2
S = L + 2pr2 = 160p + 2p(8)2
= 288p in2

16. Example 2B: Finding Lateral Areas and Surface Areas
of Right Cylinders
Find the lateral area and surface area of a right
cylinder with circumference 24p cm and a height
equal to half the radius. Give your answers in
terms of p .
Step 1 Use the circumference to find the radius.
C = 2pr Circumference of a circle
24p = 2pr Substitute 24p for C.
r = 12 Divide both sides by 2p.

17. Example 2B Continued
Find the lateral area and surface area of a right
cylinder with circumference 24p cm and a height
equal to half the radius. Give your answers in
terms of p .
Step 2 Use the radius to find the lateral area and
surface area. The height is half the radius, or 6 cm.
L = 2prh = 2p(12)(6) = 144p cm2
S = L + 2pr2 = 144p + 2p(12)2
= 432p in2
Lateral area
Surface area

18. Check It Out! Example 2
Find the lateral area and surface area of a
cylinder with a base area of 49p and a height
that is 2 times the radius.
Step 1 Use the circumference to find the radius.
A = pr2
49p = pr2
r = 7
Area of a circle
Substitute 49p for A.
Divide both sides by p and take the
square root.

19. Check It Out! Example 2 Continued
Find the lateral area and surface area of a
cylinder with a base area of 49p and a height
that is 2 times the radius.
Step 2 Use the radius to find the lateral area and
surface area. The height is twice the radius, or 14 cm.
L = 2prh = 2p(7)(14)=196p in2
S = L + 2pr2 = 196p + 2p(7)2 =294p in2
Lateral area
Surface area

20. Example 3: Finding Surface Areas of Composite
Three-Dimensional Figures
Find the surface area of the composite figure.

21. Example 3 Continued
The surface area of the rectangular prism is
.
.
A right triangular prism is added to the
rectangular prism. The surface area of the
triangular prism is
Two copies of the rectangular prism base are
removed. The area of the base is B = 2(4) = 8 cm2.

22. Example 3 Continued
The surface area of the composite figure is the sum
of the areas of all surfaces on the exterior of the
figure.
S = (rectangular prism surface area) + (triangular
prism surface area) – 2(rectangular prism base area)
S = 52 + 36 – 2(8) = 72 cm2

23. Check It Out! Example 3
Find the surface area of the composite figure.
Round to the nearest tenth.

24. Check It Out! Example 3 Continued
Find the surface area of the composite figure.
Round to the nearest tenth.
The surface area of the rectangular prism is
S =Ph + 2B = 26(5) + 2(36) = 202 cm2.
The surface area of the cylinder is
S =Ph + 2B = 2p(2)(3) + 2p(2)2 = 20p ≈ 62.8 cm2.
The surface area of the composite figure is the sum
of the areas of all surfaces on the exterior of the
figure.

25. Check It Out! Example 3 Continued
Find the surface area of the composite figure.
Round to the nearest tenth.
S = (rectangular surface area) +
(cylinder surface area) – 2(cylinder base area)
S = 202 + 62.8 — 2(p)(22) = 239.7 cm2

26. Remember!
Always round at the last step of the problem. Use
the value of p given by the p key on your
calculator.

27. Example 4: Exploring Effects of Changing Dimensions
The edge length of the cube is tripled. Describe
the effect on the surface area.

28. Example 4 Continued
24 cm
original dimensions: edge length tripled:
S = 6ℓ2
= 6(8)2 = 384 cm2
S = 6ℓ2
= 6(24)2 = 3456 cm2
Notice than 3456 = 9(384). If the length, width, and
height are tripled, the surface area is multiplied by 32,
or 9.

29. Check It Out! Example 4
The height and diameter of the cylinder are
multiplied by . Describe the effect on the
surface area.

30. Check It Out! Example 4 Continued
11 cm
7 cm
original dimensions: height and diameter halved:
S = 2p(112) + 2p(11)(14)
S = 2p(5.52) + 2p(5.5)(7)
= 550p cm2
= 137.5p cm2
Notice than 550 = 4(137.5). If the dimensions are
halved, the surface area is multiplied by

31. Example 5: Recreation Application
A sporting goods company sells tents in two
styles, shown below. The sides and floor of each
tent are made of nylon.
Which tent requires less nylon to manufacture?

32. Example 5 Continued
Pup tent:
Tunnel tent:
The tunnel tent requires less nylon.

33. Check It Out! Example 5
A piece of ice shaped like a 5 cm by 5 cm by 1 cm
rectangular prism has approximately the same
volume as the pieces below. Compare the surface
areas. Which will melt faster?
The 5 cm by 5 cm by 1 cm prism has a surface area of
70 cm2, which is greater than the 2 cm by 3 cm by
4 cm prism and about the same as the half cylinder. It
will melt at about the same rate as the half cylinder.

34. Lesson Quiz: Part I
Find the lateral area and the surface area of
each figure. Round to the nearest tenth, if
necessary.
1. a cube with edge length 10 cm
L = 400 cm2 ; S = 600 cm2
2. a regular hexagonal prism with height 15 in.
and base edge length 8 in.
L = 720 in2; S » 1052.6 in2
3. a right cylinder with base area 144p cm2 and a
height that is the radius
L » 301.6 cm2; S = 1206.4 cm2

35. Lesson Quiz: Part II
4. A cube has edge length 12 cm. If the edge
length of the cube is doubled, what happens to
the surface area?
5. Find the surface area of The surface area is mult ipthliee dc obmy p4o.site figure.
S = 3752 m2

36. All rights belong to their
respective owners.
Copyright Disclaimer Under
Section 107 of the Copyright Act
1976, allowance is made for
"fair use" for purposes such as
criticism, comment, news
reporting, TEACHING,
scholarship, and research.
Fair use is a use permitted by
copyright statute that might
otherwise be infringing.
Non-profit, EDUCATIONAL or
personal use tips the balance in
favor of fair use.