Embed presentation
Download as PDF, PPTX


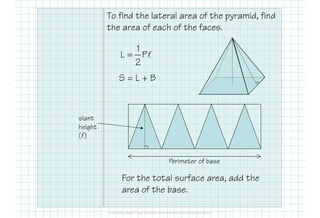

2
=
2
480 in=
2
S 480 96 3 in= +
2
646.3 in≈
5 2 m L (5)(5 2)= π
2
25 2 m= π
2
S 25 2 25 m= π + π
2
189.6 m≈](https://image.slidesharecdn.com/5-160504150727/85/5-13-5-Surface-Area-9-320.jpg)
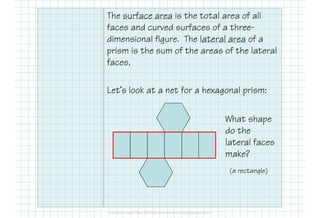
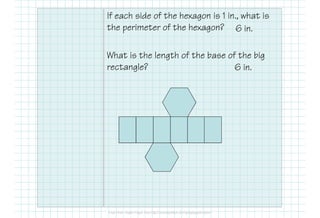
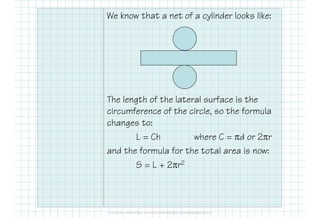
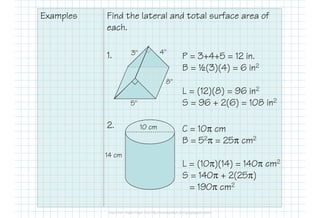
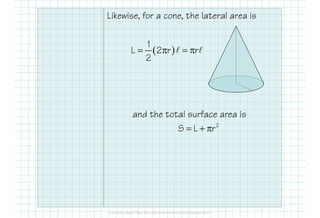
This document provides formulas and examples for calculating the surface area of various 3D shapes. It defines surface area as the total area of all faces and curved surfaces. Formulas are provided for calculating the lateral area and total surface area of prisms, cylinders, pyramids, and cones. The lateral area of prisms and cylinders is calculated using the perimeter/circumference and height. The total surface area is the lateral area plus the area of the two bases. Examples are included to demonstrate calculating the lateral and total surface area for different shapes.









2
=
2
480 in=
2
S 480 96 3 in= +
2
646.3 in≈
5 2 m L (5)(5 2)= π
2
25 2 m= π
2
S 25 2 25 m= π + π
2
189.6 m≈](https://image.slidesharecdn.com/5-160504150727/85/5-13-5-Surface-Area-9-320.jpg)