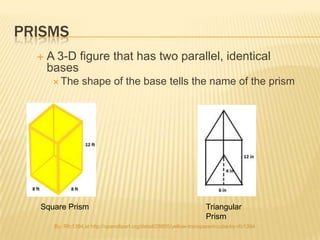
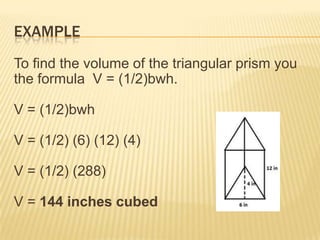
This document discusses how to calculate the volumes of various three-dimensional geometric figures. It provides formulas for finding the volumes of rectangular prisms, triangular prisms, cylinders, pyramids, and cones. Examples are given for each figure to demonstrate how to apply the volume formulas. A reference sheet at the end lists the key volume formulas for quick reference.

1. VOLUME OF THREE-DIMENSIONAL
FIGURES

2. THREE-DIMENSIONAL FIGURE
A solid, that has length, width, and
depth
Merlin2525 at http://openclipart.org/detail/117355/geometry-1-by-merlin2525

3. PRISMS
 A 3-D figure that has two parallel, identical
bases
 The shape of the base tells the name of the prism
Square Prism Triangular
Prism
By: Rfc1394 at http://openclipart.org/detail/28855/yellow-transparent-cube-by-rfc1394

4. PYRAMID
 3-D figure that has one base, all other faces
are triangles that share the same vertex
(point)
 Name of the base names the pyramid
Pentagonal Pyramid
roym at http://openclipart.org/detail/15237/pyramide-by-roym

5. CYLINDERS
A 3-D solid that has two parallel, identical circular
bases
gswanson at http://openclipart.org/detail/7498/storage-cylinder-by-gswanson

6. CONES
A cone is a 3-D solid that has one circular base
and one vertex.
pascallapalme at http://openclipart.org/detail/35731/cone-by-pascallapalme

7. FINDING THE VOLUME OF THREE-
DIMENSIONAL FIGURES

8. VOLUME OF RECTANGULAR PRISMS
 The formula to find the volume of a
rectangular prism is V = lwh.
 Take the length (l) of the rectangular prism
and multiply it by the width (w) and then by
the height (h).
 Your answer will always be units cubed.

9. EXAMPLE
 To find the volume of the rectangular
prism use the formula V =lwh.
 You multiply 8 x 8 x 12.
 Your final answer is 768 feet cubed.
By: Rfc1394 at http://openclipart.org/detail/28855/yellow-transparent-cube-by-rfc1394

10. VOLUME OF TRIANGULAR PRISMS
To find the volume of a triangular
prism you use the formula:

11. EXAMPLE
To find the volume of the triangular prism you
the formula V = (1/2)bwh.
V = (1/2)bwh
V = (1/2) (6) (12) (4)
V = (1/2) (288)
V = 144 inches cubed

12. VOLUME OF A CYLINDER
To find the volume of a cylinder you will use the
formula:

13. EXAMPLE
To find the volume of the cylinder we need to
use the formula
V = Bh.
The area of the base of a cylinder is a
circle.
Use 3.14 x the radius squared x the height.
V = (3.14) (4 x 4) (10)
V = 502.4 ft cubed
gswanson at http://openclipart.org/detail/7498/storage-cylinder-by-gswanson

14. VOLUME OF A PYRAMID
To find the volume of a pyramid you use the
following formula:

15. EXAMPLE
 To find the volume of a pyramid you use the formula:
(1/3)Bh.
 The "B" stands for the area of the base.
 The pyramid gives us the area of the base and the
height.
 To find the volume of the pyramid we need to:
V = (1/3) (56) (32)
Multiply 56 and 32.
Then divide by 3.
V = 597.3 mm cubed

16. VOLUME OF A CONE
To find the volume of a cone, use the following
formula.

17. EXAMPLE
To find the volume of the cone we will use the formula
V = (1/3)Bh
V = (1/3) (3.14) (r x r) (h)
V = (1/3) (3.14) (6) (6) (10)
V = (1/3) (3.14) (360)
V = (1/3) (1130.4)
V = 376.8 ft cubed
pascallapalme at http://openclipart.org/detail/35731/cone-by-pascallapalme

18. VOLUME FORMULA REFERENCE SHEET
Rectangular Prism Triangular Prism
V = lwh
Cylinder
Pyramid
Cone

19. REFERENCES
Clip art from openclipart.org
 Merlin2525 at
http://openclipart.org/detail/117355/geometry-1-by-
merlin2525
 Rfc1394 at http://openclipart.org/detail/28855/yellow-
transparent-cube-by-rfc1394
 Roym at http://openclipart.org/detail/15237/pyramide-by-
roym
 Gswanson at http://openclipart.org/detail/7498/storage-
cylinder-by-gswanson
 Pascallapalme at http://openclipart.org/detail/35731/cone-
by-pascallapalme
All Clipart not cited in a footnote and on this reference page I
created using Paint.