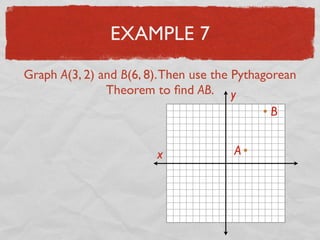
This document defines key vocabulary terms related to line segments and distance, including line segment, betweenness of points, congruent segments, and distance formula. It provides examples of calculating distances between points on number lines and using the Pythagorean theorem to find distances between points graphed on a coordinate plane. Examples include measuring line segments with a ruler, finding distances by adding or subtracting measures, and applying the distance formula and Pythagorean theorem to solve for unknown distances.