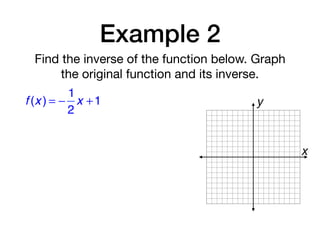
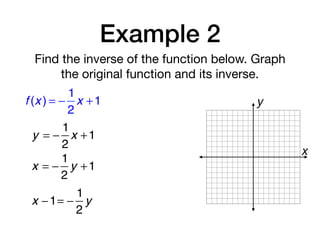
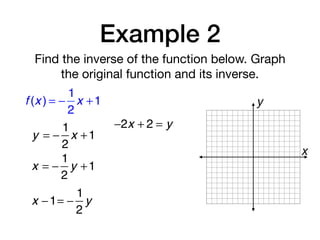
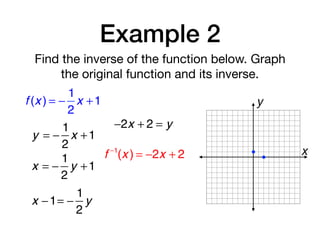
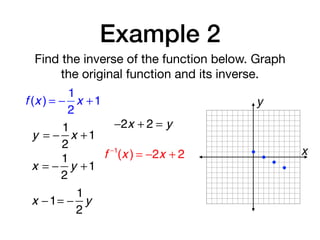
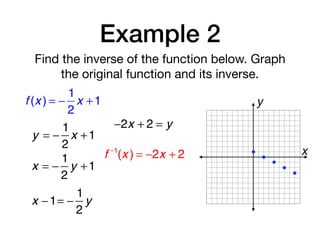
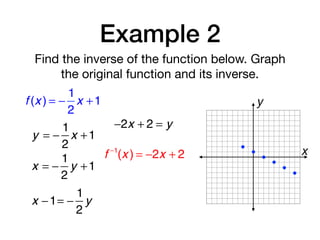
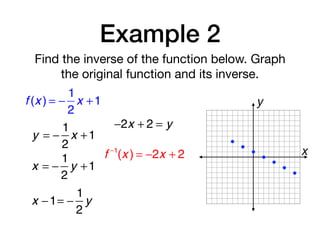
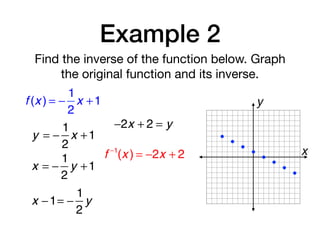
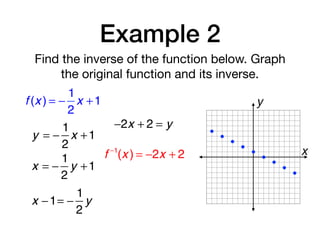
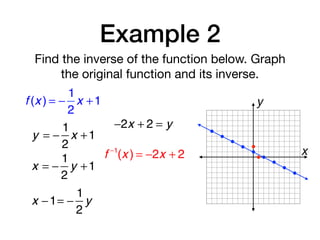
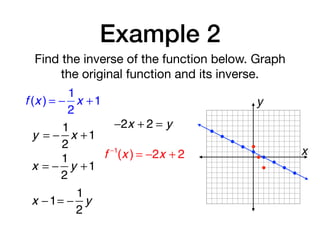
The document discusses inverse functions and relations. It defines an inverse relation as one where the coordinates of a relation are switched, and an inverse function as one where the domain and range of a function are switched. It provides examples of finding the inverse of specific relations and functions by switching their coordinates or domain and range. It also discusses how to determine if two functions are inverses using their graphs and the horizontal line test.










































![Example 3
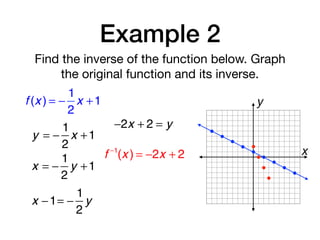
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-59-320.jpg)
![Example 3
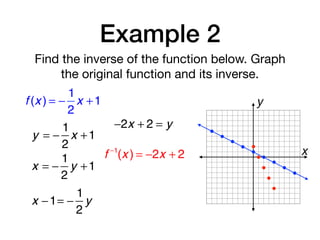
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-60-320.jpg)
![Example 3
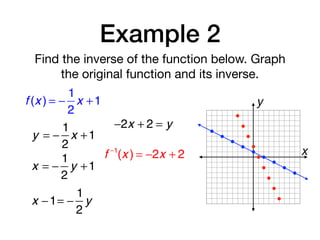
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-61-320.jpg)
![Example 3
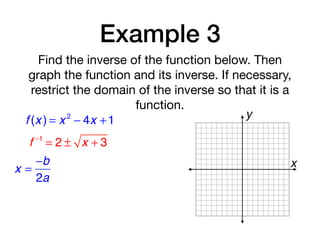
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-62-320.jpg)
![Example 3
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-63-320.jpg)
![Example 3
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-64-320.jpg)
![Example 3
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-65-320.jpg)
![Example 3
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-66-320.jpg)
![Example 3
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-67-320.jpg)
![Example 3
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-68-320.jpg)
![Example 3
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-69-320.jpg)
![Example 3
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-70-320.jpg)
![Example 3
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-71-320.jpg)
![Example 3
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-72-320.jpg)
![Example 3
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-73-320.jpg)
![Example 3
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-74-320.jpg)
![Example 3
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-75-320.jpg)
![Example 3
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-76-320.jpg)
![Example 3
Find the inverse of the function below. Then
graph the function and its inverse. If necessary,
restrict the domain of the inverse so that it is a
function.
f (x ) = x 2
− 4x +1
f −1
= 2 ± x + 3
x =
−b
2a
x =
4
2
x = 2
f −1
= 2 + x + 3; (−∞,2]
f −1
= 2 − x + 3; [2,+∞)
x
y](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-77-320.jpg)


 = x and [g !f ](x ) = x](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-80-320.jpg)
 = x and [g !f ](x ) = x
f (x ) =
3
4
x − 6](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-81-320.jpg)
 = x and [g !f ](x ) = x
f (x ) =
3
4
x − 6 g(x ) =
4
3
x + 8](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-82-320.jpg)

](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-84-320.jpg)

= f [g(x )]](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-85-320.jpg)

= f [g(x )]
= f
4
3
x + 8
⎛
⎝⎜
⎞
⎠⎟](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-86-320.jpg)

= f [g(x )]
= f
4
3
x + 8
⎛
⎝⎜
⎞
⎠⎟
=
3
4
4
3
x + 8
⎛
⎝⎜
⎞
⎠⎟ − 6](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-87-320.jpg)

= f [g(x )]
= f
4
3
x + 8
⎛
⎝⎜
⎞
⎠⎟
=
3
4
4
3
x + 8
⎛
⎝⎜
⎞
⎠⎟ − 6
= x + 6 − 6](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-88-320.jpg)

= f [g(x )]
= f
4
3
x + 8
⎛
⎝⎜
⎞
⎠⎟
=
3
4
4
3
x + 8
⎛
⎝⎜
⎞
⎠⎟ − 6
= x + 6 − 6
= x](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-89-320.jpg)

= f [g(x )]
= f
4
3
x + 8
⎛
⎝⎜
⎞
⎠⎟
=
3
4
4
3
x + 8
⎛
⎝⎜
⎞
⎠⎟ − 6
= x + 6 − 6
= x
[f ! g](x ) = x](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-90-320.jpg)

](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-92-320.jpg)

= g[f (x )]](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-93-320.jpg)

= g[f (x )]
= g
3
4
x − 6
⎛
⎝⎜
⎞
⎠⎟](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-94-320.jpg)

= g[f (x )]
= g
3
4
x − 6
⎛
⎝⎜
⎞
⎠⎟
=
4
3
3
4
x − 6
⎛
⎝⎜
⎞
⎠⎟ + 8](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-95-320.jpg)

= g[f (x )]
= g
3
4
x − 6
⎛
⎝⎜
⎞
⎠⎟
=
4
3
3
4
x − 6
⎛
⎝⎜
⎞
⎠⎟ + 8
= x − 8 + 8](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-96-320.jpg)

= g[f (x )]
= g
3
4
x − 6
⎛
⎝⎜
⎞
⎠⎟
=
4
3
3
4
x − 6
⎛
⎝⎜
⎞
⎠⎟ + 8
= x − 8 + 8
= x](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-97-320.jpg)

= g[f (x )]
= g
3
4
x − 6
⎛
⎝⎜
⎞
⎠⎟
=
4
3
3
4
x − 6
⎛
⎝⎜
⎞
⎠⎟ + 8
= x − 8 + 8
= x
[g !f ](x ) = x](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-98-320.jpg)

 = x [g !f ](x ) = x](https://image.slidesharecdn.com/alg2section5-3-180529224928/85/Algebra-2-Section-5-3-100-320.jpg)