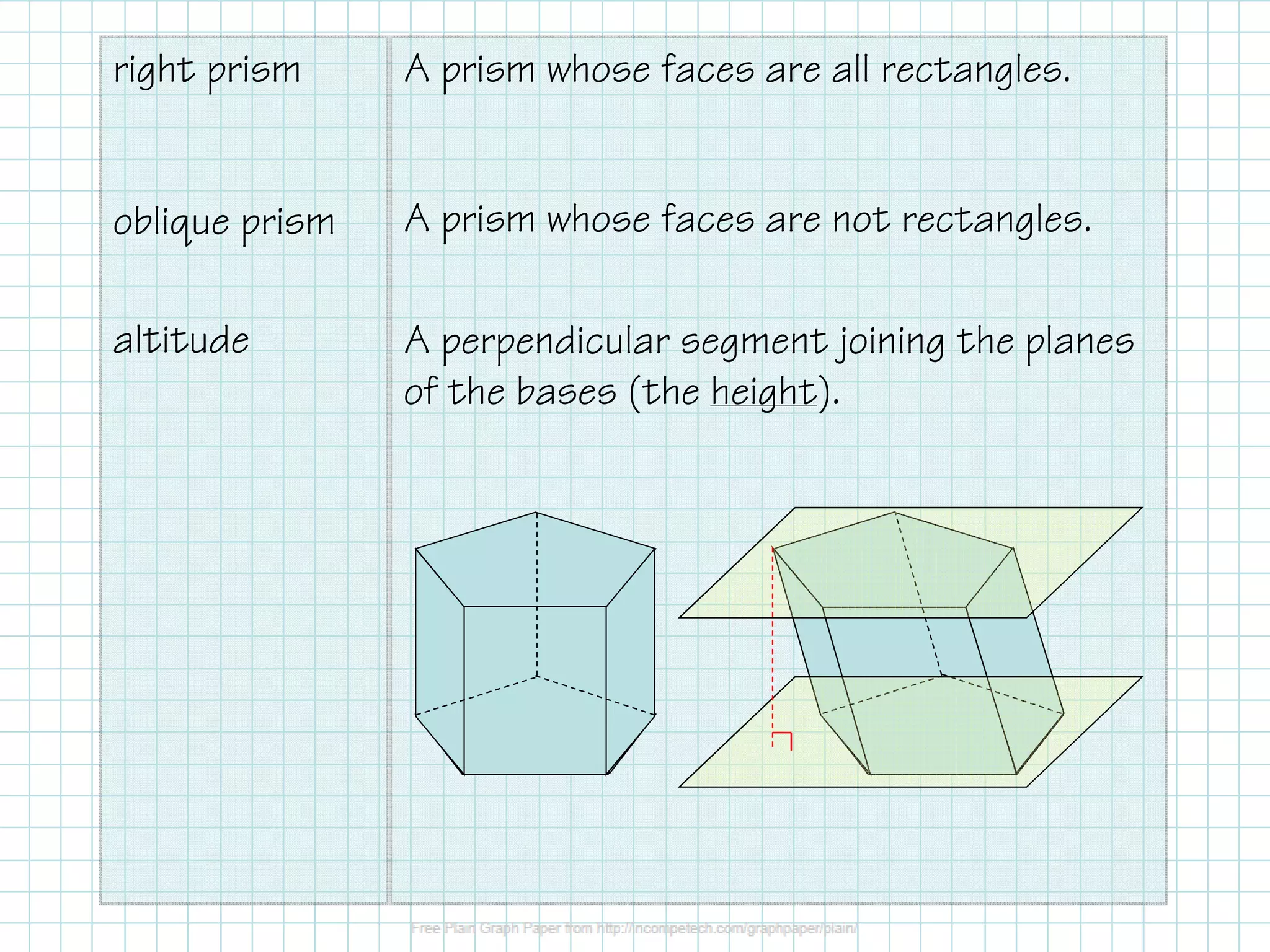
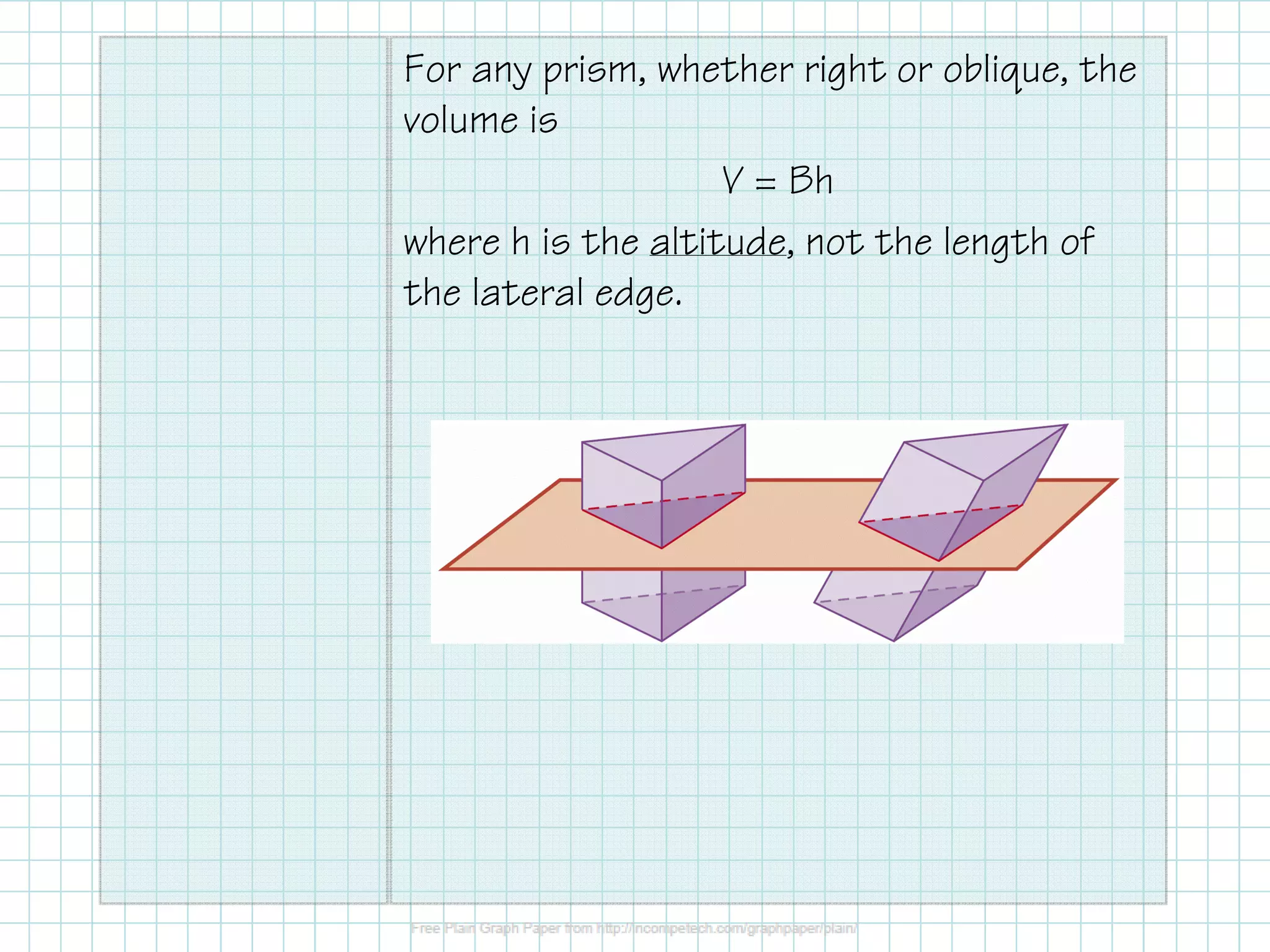
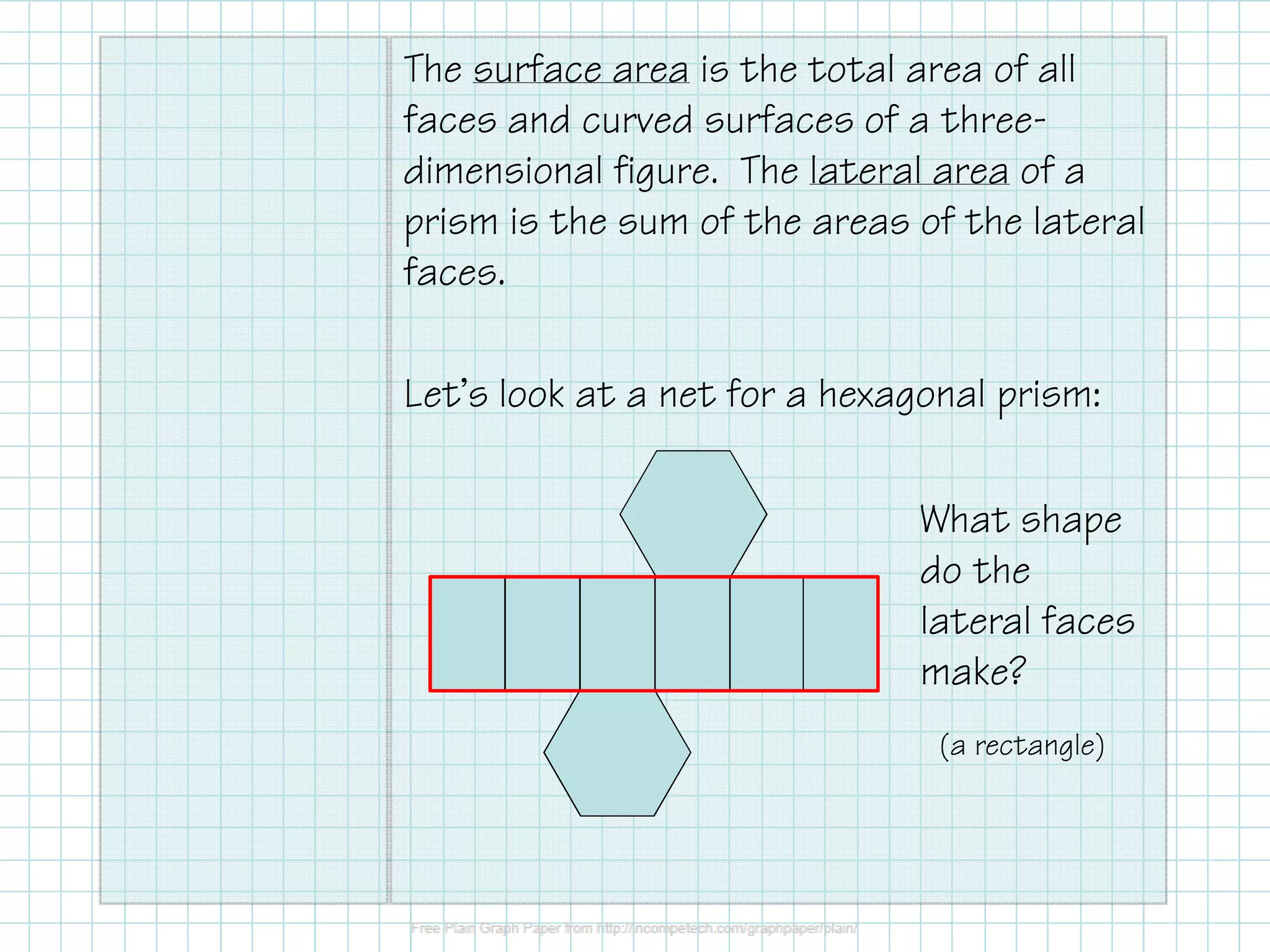
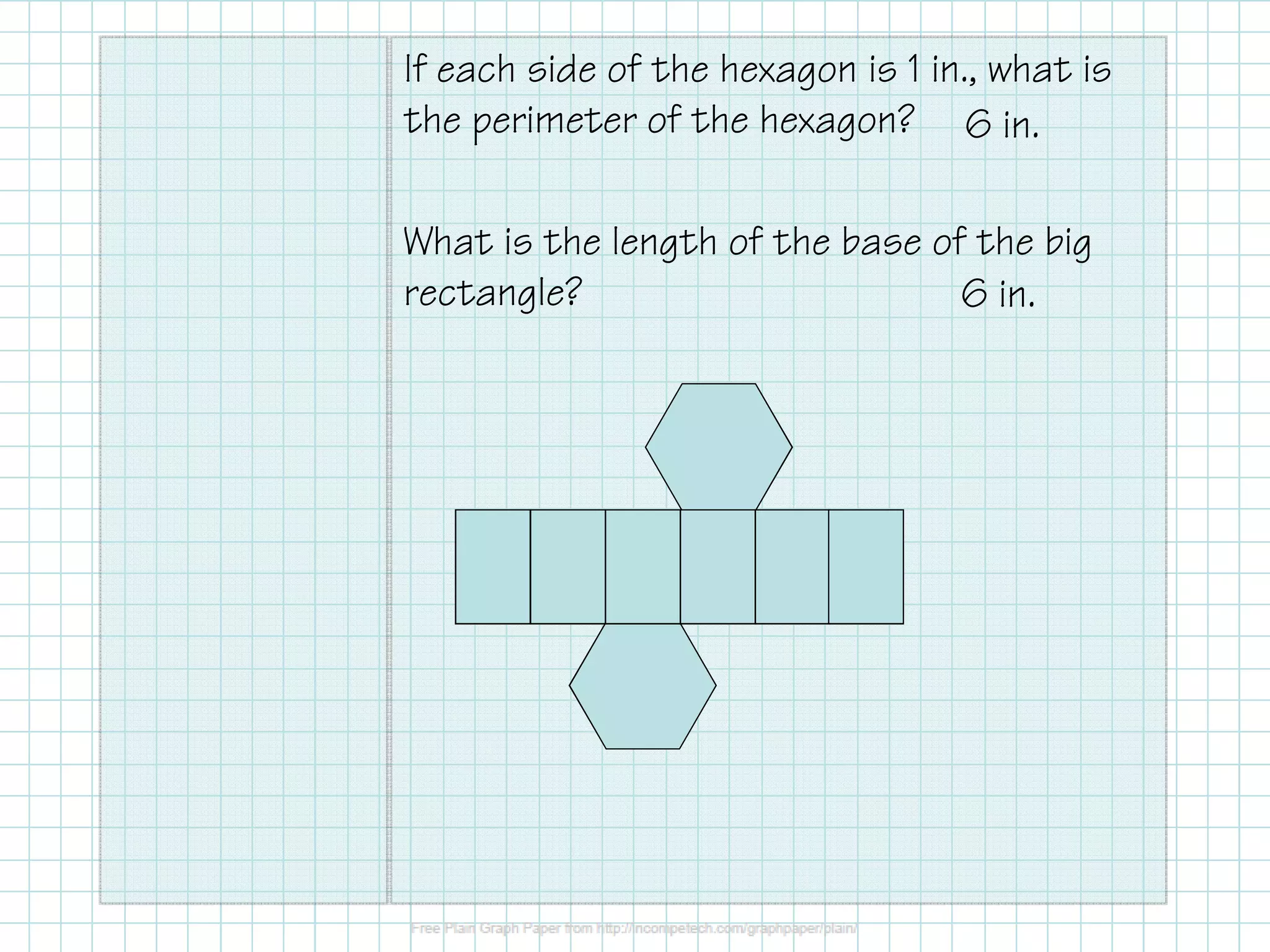
This document provides information about calculating the surface area and volume of prisms and cylinders. It defines right and oblique prisms, and explains that the volume formula is the same for both as V=Bh, where B is the base area and h is the altitude or height. The same is true for cylinders, where the volume is V=πr^2h. Examples are given to find the volume of various prisms and cylinders. Formulas are also provided for calculating the lateral and total surface area of prisms as S=L+2B, where L is the lateral area calculated as L=Ph, and B is the base area. For cylinders, the lateral area formula is L=C*h,

1. Obj. 51 Prisms and Cylinders
The student is able to (I can):
• Calculate the surface area and volume of prisms and
cylinders

2. right prism
oblique prism
altitude
A prism whose faces are all rectangles.
A prism whose faces are not rectangles.
A perpendicular segment joining the planes
of the bases (the height).

3. Let’s consider a deck of cards. If a deck is
stacked neatly, it resembles a right
rectangular prism. The volume of the prism
is
V = Bh,
where B is the area of one card, and h is
the height of the deck.
If we shift the deck so
that it becomes an
oblique prism, does it
have the same number
of cards?

4. For any prism, whether right or oblique, the
volume is
V = Bh
where h is the altitude, not the length of
the lateral edge.

5. Likewise, for cylinders, it doesn’t matter
whether the cylinder is right or oblique, the
volume is
V = Bh = πr2h

6. Examples Find the volume of each figure:
1.
2.
10 ft.
8 ft.
3 m
19 m
( )2 2
B 3 9 m= π = π
3
V (9 )(19) 171 m= π = π
( )
1 5
B 50 172.05
2 tan36
 = = 
° 
V = (172)(8) = 1376 ft3

7. The surface area is the total area of all
faces and curved surfaces of a three-
dimensional figure. The lateral area of a
prism is the sum of the areas of the lateral
faces.
Let’s look at a net for a hexagonal prism:
What shape
do the
lateral faces
make?
(a rectangle)

8. If each side of the hexagon is 1 in., what is
the perimeter of the hexagon?
What is the length of the base of the big
rectangle?
6 in.
6 in.

9. This relationship leads to the formula for
the lateral area of a prism:
L = Ph
where P is the perimeter and h is the height
of the prism.
For the total surface area, add the areas
of the two bases:
S = L + 2B

10. We know that a net of a cylinder looks like:
The length of the lateral surface is the
circumference of the circle, so the formula
changes to:
L = Ch where C = πd or 2πr
and the formula for the total area is now:
S = L + 2πr2

11. Examples Find the lateral and total surface area of
each.
1.
2. 10 cm
14 cm
4"3"
8"
5"
P = 3+4+5 = 12 in.
B = ½(3)(4) = 6 in2
L = (12)(8) = 96 in2
S = 96 + 2(6) = 108 in2
C = 10π cm
B = 52π = 25π cm2
L = (10π)(14) = 140π cm2
S = 140π + 2(25π)
= 190π cm2