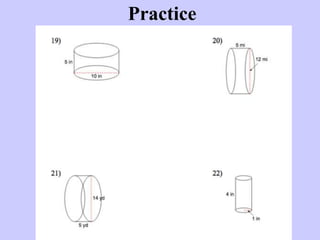
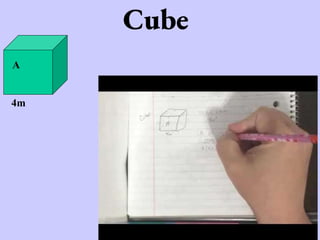
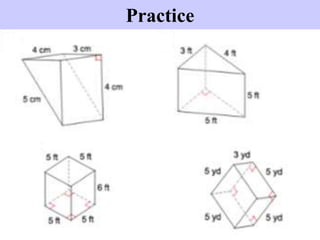
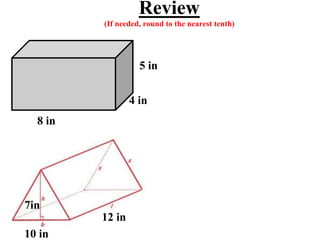
The document provides information on calculating surface area for different shapes including prisms, cylinders, and compound figures. It defines surface area as the total area of all sides of an object. Formulas are provided for finding the surface area of rectangular and triangular prisms, cubes, cylinders, and compound figures made of multiple attached shapes. Examples are worked through demonstrating how to use the formulas and which areas to include or exclude when objects are combined.

1. Surface Area
• Surface area is found by finding the area of
all the sides and then adding those answers
up.
• How will the answer be labeled?
– Units2 because it is area!

2. SA
• You can find the SA of any prism by using
the basic formula for SA which is
• 2B + LSA= SA
• LSA= lateral Surface area
• LSA= perimeter of the base x height of the
prism
• B = the base of the prism.

3. Rectangular Prism
Step 1: How many faces (sides)
are on here? 6
Step 2: Find the area of each
of the faces.
A
B
C
4
5
in
6 Do any of the faces have
the same area?
A = 5 x 4 = 20 x 2 =40
C = 6 x 5 = 30 x 2 = 60
B = 4 x 6 = 24 x 2 = 48
If so, which ones?
148 in2
Opposite faces are the same.
Find the SA Step 3: Find the sum of the
area of each of the faces.
“How to” video on next slide
● Top and Bottom (B)
● Left and Right (C)
● Front and Back (A)

4. Rectangular Prism
A
B
C
4
5
in
6
A = 5 x 4 = 20 x 2 =40
C = 6 x 5 = 30 x 2 = 60
B = 4 x 6 = 24 x 2 = 48
148 in2
Find the SA

5. Cube
Are all the faces the same? YES
4m How many faces are there?
6
Find the Surface area of
one of the faces.
A
4 x 4 = 16
Take 16 and multiply by
the number of faces.
x 6
SA for a cube.
“How to” video on next slide
96 m2

6. Cube
4m
A

7. Triangular Prisms
• Use the same triangular prism seen on the last slide.
Let’s us the formula this time. 2B + LSA=SA
• Find the area of the base, which is a triangle because it
is a triangular prism. You will need two of them.
• Now, find the perimeter of that same base and multiply
it by how many layer of triangles are in the picture.
That is the LSA.
• Add that to the two bases. Now you should have the
same answer as before.
• Either way is the correct way.

8. Triangular Prism
How many faces are
there? 5
How many of each shape does it
take to make this prism?
2 triangles and 3 rectangles = SA of a
triangular prism
4
3
5
10 m
Find the surface area. Start by
finding the area of the triangle.
(4 x 3) / 2 = 6
How many triangles were
there? 2
x 2= 12
Find the area of the 3
rectangles.
5 x 10 = 50 = front
4 x 10 = 40 = back
3 x 10 = 30 = bottom
SA = 132 m2
What is the final SA?
“How to” video on next slide

9. Triangular Prism
4
3
5
10 m
x 2= 12
5 x 10 = 50 = front
4 x 10 = 40 = back
3 x 10 = 30 = bottom
SA = 132 m2
(4 x 3) / 2 = 6

10. Practice

11. Practice...answers

12. Review
(If needed, round to the nearest tenth)
8 in
4 in
5 in
10 in
12 in
7in

13. 6 faces
All rectangles
5 faces
2 triangle bases
3 rectangles
3 faces
2 circle bases
1 rectangle side
2B + LSA
2 (LxW) + (L+W+L + W) x H
2B + LSA
2 [½ (AxB)] + (A+B+C) x H
A
B
C
L
W
2B + LSA
2 (𝛑 r² ) + (𝛑 D) x H
Diameter radius
Surface Area
𝛑 = 3.14

14. Cylinders
6
10m
What does it take to make this?
2 circles and 1 rectangle= a cylinder
2 B 3.14 x 9 = 28.26 X 2 = 56.52
+ LSA(p x H) 3.14 x 6 =18.84 x 10 = 188.4
SA = 244.92
2B + LSA = SA
“How to” video on next slide

15. Cylinders
6
10m
What does it take to make this?
2 circles and 1 rectangle= a cylinder
3.14 x 9 = 28.26 X 2 = 56.52
3.14 x 6 =18.84 x 10 = 188.4
SA = 244.92
2B + LSA = SA

16. Practice

17. Practice Answers

18. Intro to Compound Figures
Finding the total surface area
for when you want to wrap 2
rectangular prisms together…
How much paper would be
required?
Video is easiest to be seen when in
“Full Screen”

19. Compound Figures
a figure made up of 2 or more shapes
=
+
=

20. 1. Determine what regular shapes make up the compound
shape
1. Find the surface area of each shape, but make sure you
only account for the space being covered since the two
shapes are attached as one…
a. The shape DOES NOT come apart
1. p
2. You do not need to account for the
bottom of the cylinder, nor do you
need the circle the cylinder makes
on the top face of the rectangular
prism.
a. these surface are not seen nor
are they covered since the
shapes are attached
The circular base of the cylinder is not accounted for
nor is the space on the rectangular prism that the circle
sits on. These areas do not count since the two shapes
are attached and therefore you would not cover these
areas individually