The document covers the geometric measurement of three-dimensional figures, defining polyhedrons, prisms, pyramids, cylinders, cones, and spheres, along with methods for calculating their surface areas and volumes. It includes various formulas for calculating both surface area and volume for different solids, as well as examples for application. Additionally, the document provides completion and matching exercises to reinforce the concepts presented.

1. Measurement of Three-dimensional Figures
Polyhedron is a solid figure with no curved sides. It is bounded by polygons as its
surfaces. The flat surfaces from by polygons and their interior are called faces. Faces
intersect at line segments called edges. Two or more edges intersect at a point called
vertex.
The polygon t the left has 4
faces, 6 edges and 4 vertices. It
is called a tetrahedron
edge
face
vertex
A Prism is a polyhedron whose
bases are congruent and parallel
and whose lateral faces are
parallelogram. The prism at the
left has 2 bases and 4 lateral
faces.
lateral faces
base

2. A Pyramid is a polyhedron with a polygon as base and triangles as lateral faces.
The most common pyramids are those with triangles, square and, rectangles as bases.
A Cube is a regular prism
because it is bounded by a
regular polygon (square) and all
its angles are right angles.
vertex
face
edge
A Rectangular solid is the most
common type of right prism. It
is bounded by rectangles whose
corners are right angles.face
triangular
pyramid
square
pyramid
rectangular
pyramid

3. A Cylinder is a solid whose bases are congruent circles. A right circular cylinder
is a cylinder whose altitude is perpendicular to the bases and has an endpoint in each
base.
A Cone is a solid with a circle as base and all line segments from the circle meet
at a point called the vertex. A right circular cone is a cone whose altitude is a segment
that is perpendicular to the base. Any segment that joins the vertex to a point on the circle
is a slant height.
A Sphere is a solid with all points of which are equidistant from the fixed point called the
centre. A radius of a sphere is a segment whose endpoints are the centre and a point on
the sphere. CD is a radius. A chord of a sphere is a segment whose endpoints are points
on the sphere. MN is a chord. A diameter of a sphere is a segment that contains the centre
and whose endpoints on the sphere. PR is a diameter. A tangent to a sphere is a line that
intersects the sphere in exactly one point. XY is a tangent to the sphere at O.
O Y
X
lateral face
altitude
radius
radius
base
altitude
slant height
base
C
P
R
D
M
N

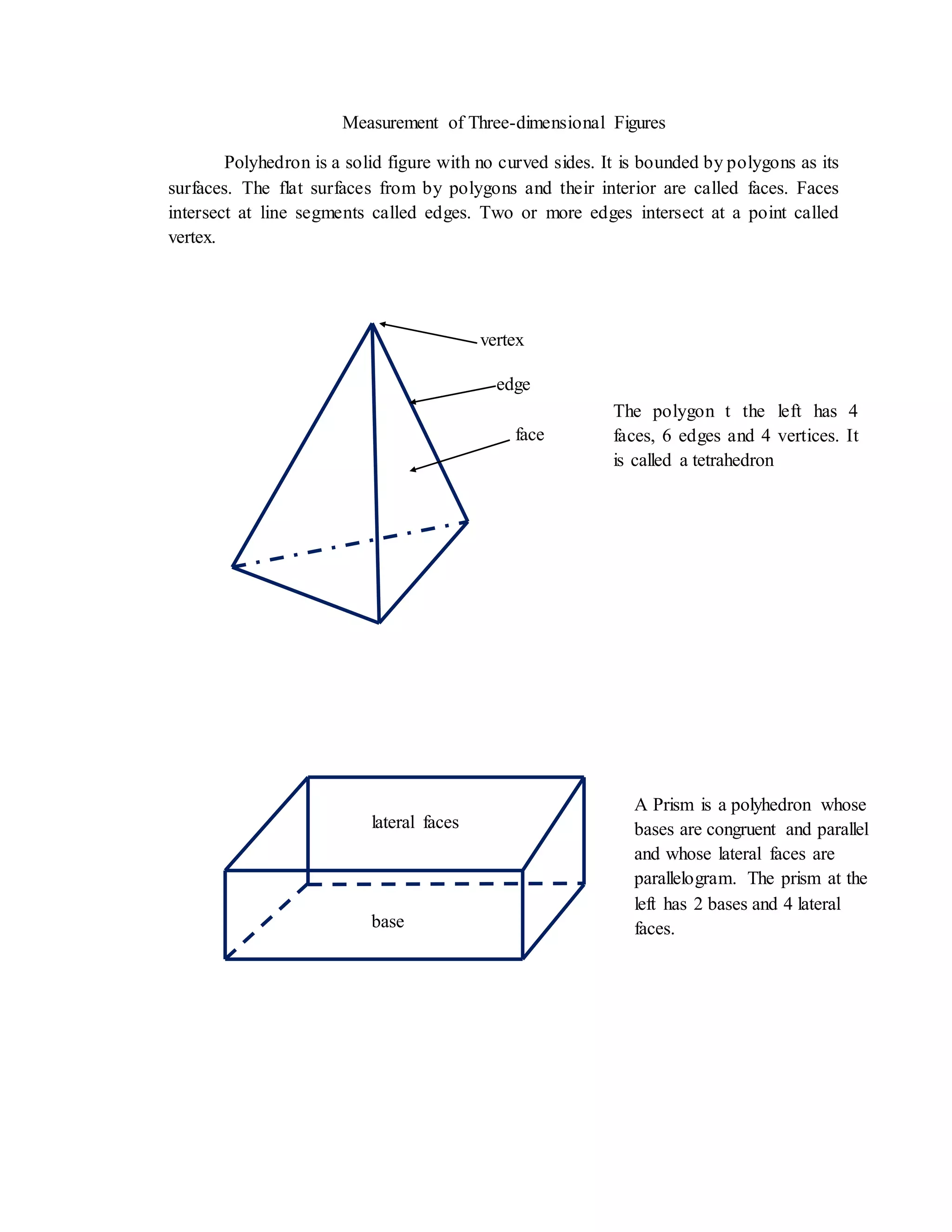
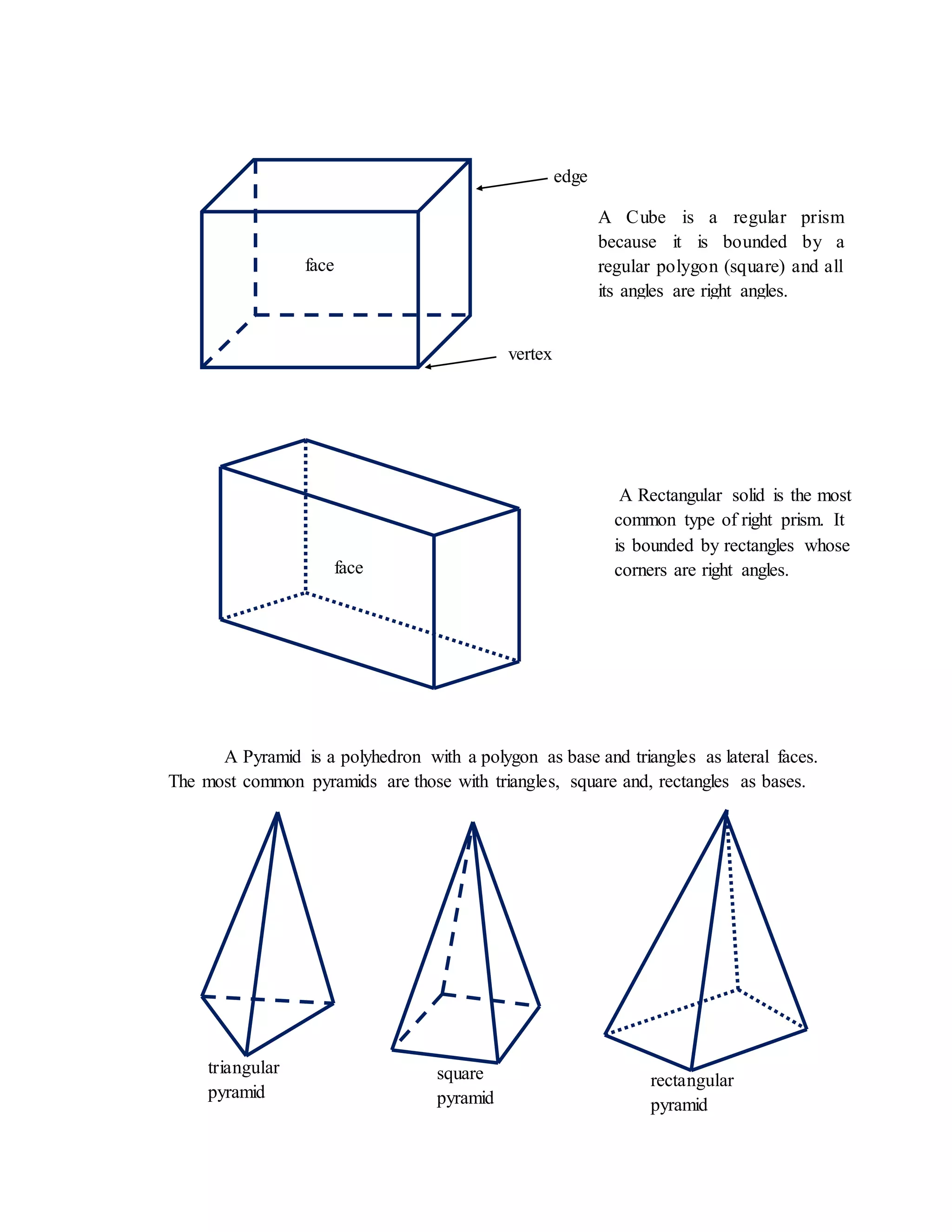
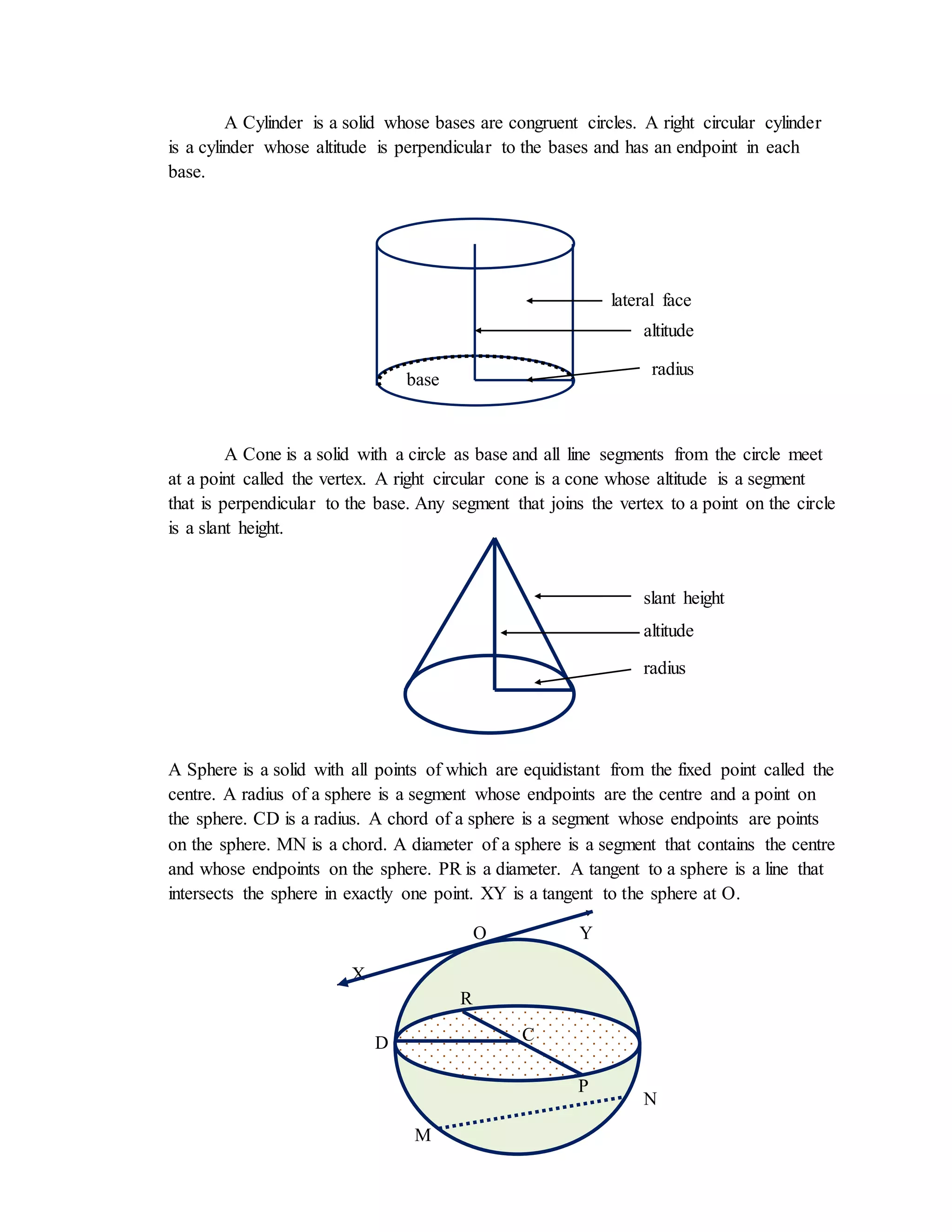
4. Measurements of 3D Figures
Surface Are of Solids is defined as the sum of the areas of the outer surfaces of a solid.
These outer faces are known as faces.
A. Surface Area of a Cube. To find the surface area of a cube, multiply the square f
the length of a side by 6.
B. Surface Area of Rectangular Prism is the total area of the surfaces of rectangular
prism.
Formula;
SA = 6s2
Where s is the side or the edge of the cube
Example;
1. s = 2.2cm
SA = 6s2
= 6(2.2cm) 2
= 6(4.84cm2)
SA = 29.04cm2
2. s = 0.09m
SA = 6s2
= 6(0.09cm)2
= 6(0.0081m2)
SA = 0.0486m2
Formula:
SA = 2B + LA
where B is the area of the base
LA is the area of the lateral faces
Examples:
1. Find the surface area of a rectangular prism whose length is 7cm,
width is 4cm and thickness is 5cm.
SA = 2B + LA
SA = 2(lw + lh + wh)
= 2[(7cm)(4cm) + (4cm)(5cm) + (7cm)(5cm)]
= 2(28cm2 + 20cm2 + 35cm2)
= 2(83cm2)
SA = 166cm2
2. L = 12cm, w =7cm and h = 6cm
SA = 2B + LA
SA = 2(lw + lh + wh)
= 2(12cm x 7cm) + 2(7cm x 6cm) + 2(12cm x 6cm)
= 168cm2 + 84cm2 + 144cm2
SA = 396cm2

5. C. Surface Area of Cylinder is the amount of spaces outside the sphere.
D. Surface Area of a Cone is the amount of space outside the cone.
E. Surface Area of Sphere is the amount of space outside the sphere.
Formula;
SA = 2Лr2 + 2Лrh or SA = 2Лr(r + h)
where r is the radius
h is the height
Example:
1. Find the surface are of a cylinder having radius is equal to 7cm and
height is 20m.
SA = 2Лr2 + 2Лrh
= 2(3.14) (5cm)2 + 2(3.14)(5cm)(20cm)
= 2(3.14) (25cm2) + 2(3.14)(100cm2)
= (6.28) (25cm2) + (6.28) (100cm2)
= 157cm2 + 628cm2
SA = 785cm2
Formula:
SA = Лr2 + Лrs
where s is the slant height
and r is the radius of the base
Example:
1. Find the surface area of a cone having s = 7.25cm and r = 3.5cm.
SA = Лr2 + Лrs
= (3.14) (3.5cm)2 + (3.14) (3.5cm) (7.25cm)
= (3.14) (12.25cm2) + (10.99cm2) (7.25)
= 38.465cm2 + 79.6775cm2
SA = 118.1425cm2
Formula:
SA = 4Лr2
where r is the radius
Example:
1. Find the surface area of a sphere having r = 6cm.
SA = 4Лr2
= 4(3.14) (6cm)2
= 12.56 (36cm2)
SA = 452.16cm2

6. F. Surface Area of Square Pyramid is the amount of space outside the square
pyramid.
Volume is used to measure space. It is the amount of space enclosed in a solid figure. It is
expressed in cubic denominations.
G. Volume of a Rectangular Prism is the amount of space enclosed in rectangular
prism.
Formula:
SA = s2 + 2bs
where s2 is the area of the base
b side of the base
s is the slant height
Example:
1. Find the surface area of the square pyramid having b = 3cm, s = 5cm
and s2 = (3cm)2.
SA = s2 + 2bs
= (3cm)2 + 2(3cm)(5cm)
= 9cm2 + 30cm2
SA = 39cm2
Formula:
V = l x w x h or area of the base times height SA = B x h
where l is the length
w is the width
h is the height
Example:
1. Find the length of the rectangular prism having l = 4.2cm, w = 3.7cm
and h = 2.5cm.
V = l x w x h
= (4.2cm) (3.7cm) (2.5cm)
= 15.54cm2 (2.5cm)
V = 38.85cm3

7. H. Volume of Triangular Prism is the amount of space enclosed in triangular prism.
I. Volume of Square a Pyramid is the amount of space enclosed in a square
pyramid.
Formula:
V = bh x H
2
Where b is the length of one side of the base
h is the height of the altitude triangular prism
H is the height of the base
Example:
1. Find the volume of triangular prism having l = 3.4cm, b = 3cm and h =
3.2cm.
V = bh x H
2
= (3.4cm) (3.2cm) x 3cm
2
= 10.88cm2 x 3cm
2
= 5.44cm2 x 3cm
V = 16.32cm3
Formula:
V = 1 (l x w) h
3
Where l is the length
w is the width
h is the height
Example:
1. Find the volume of a pyramid having l = 9cm, w = 8cm and h = 7cm.
V = 1 (l x w) h
3
= 1 (8cm x 9cm) x 7cm
3
= 1 (72cm2) x 7cm
3
= 24cm2 x 7cm
V = 168cm2
In the case of square pyramid the length and the width are equal.

8. J. Volume of a Cylinder is the amount of space enclosed in a cylinder.
K. Volume of a Cone is the amount of space enclosed in a cone.
L. Volume of a Sphere is the amount of space enclosed in a sphere.
Formula:
V = Лr2h
Where is the height
Example:
1. Find the volume of a cylinder having r = 3cm and h = 10cm.
V = Лr2h
= (3.14) (3cm)2 (10cm)
= (3.14) (90cm3)
V= 282.6cm3
Formula:
V = 1 Лr2h
3
Where r is the radius
h is the height
Example:
1. Find the surface area of a cone having the r = 3cm and h = 6cm.
V = 1 Лr2h
3
= 1 (3.14) (3cm)2 (6cm)
3
= 1 (3.14) (9cm2) (6cm)
3
= 1 (3.14) (54cm3)
3
= 169.56cm3
3
V = 56.52cm3
Formula:
V = 4Лr3
3
Example:
1. Find the volume of a sphere having h = 0.9cm.
V = 4Лr3
3
= 4 (3.14) (0.9cm)3
3
V = 3.05cm3

9. Completion
Directions: Complete the following statements by filling your answers on the blank
provided.
1. A solid figure which is bounded by polygon in each space is called
______. (polyhedron)
2. The flat surfaces form by polygons and their interior are called _______.
(faces)
3. The faces of polyhedron intersect t line segments called _________
(edges).
4. The edges of a polyhedron intersect at points called _________. (vertices)
5. A polyhedron whose bases are congruent and parallel and whose lateral
faces are parallelogram is called _______. (prism)
6. A regular prism which is bounded by squares whose corners are right
angles is called _______. (cube)
7. A right prism which is bounded by rectangles whose corners are right
angles is called ________. (rectangular solid)
8. A polyhedron with a polygon as base and triangles as lateral faces is called
_________. (pyramid)
9. A solid figure whose bases are congruent circles is called _______.
(cylinder)
10. A solid figure with a circle as base and all line segments from the circle
meet at the vertex is called ________. (cone)

10. Short Answer
Directions: Supply of what is asked in each statement.
1. What kind of cylinder whose altitude is a segment that is perpendicular to
the bases and has an endpoint in each base? (right circular cylinder)
2. What kind of four sided polygon that usually made up the faces of
rectangular solid? (rectangle)
3. What kind of pyramid that has rectangle as its base? ( rectangular
pyramid)
4. What kind of a solid figure which all points are equidistant from the given
point called center? (sphere)
5. What is the sum of the areas of the outer surfaces of a solid figure?
(surface area)
6. What is the amount of space enclosed in a solid figure? (volume)
7. What is the formula in getting the surface area of a cylinder? (SA = 2Лr2 +
2Лrh)
8. What is the formula in getting the surface area of a cone? (SA = Лr2 + Лrs)
9. What is the formula in getting the volume of a square or rectangular
pyramid? (V= 1/3 (l x w) h or V = 1/3 B x h)
10. What is the formula in getting the volume of a sphere? ( V = 4/3 Лr3)

11. Essay
Directions: Answer the following statements/questions.
1. In five sentences, write an essay describing the solid figures.
2. In four to six sentences, write an essay comparing the surface area and the volume
of a solid figure.
3. In five sentences, write an essay describing the formula and its importance in the
real world.

12. Multiple Choice
Directions: Answer the following. Encircle the correct answers.
1. What is the missing in this formula in finding the volume of a cylinder?
V = Лr2
A. w
B. l
C. b
D. h*
2. What is the missing in this formula in finding the surface area of a cone?
SA = r2 + Лrs
A. Л*
B. b
C. l
D. h
3. What is the missing in this formula in finding the volume of a sphere?
V = Лr3
A. 1/3
B. 1/2
C. 4/3*
D. 2/3
4. It is a solid figure with a circle as base and all line segments from the circle meet
at a point called the vertex. What solid figure is referred above?
A. Cone*
B. Sphere
C. Pyramid
D. Cylinder
5. What is the surface area of a cone having slant height equal to 7.25cm and radius
equal to 3.5m?
A. 118.1370cm2
B. 118.1425cm2*
C. 118.2000cm2
D. 118.1480cm2

13. 6. What is the volume of a triangular prism having length equal to 3.4cm, height of
base is 3cm and height of the prism is 3.2cm?
A. 16.35cm3
B. 16.20cm3
C. 16.32cm3*
D. 16.30cm3
7. What is the height of square pyramid having length equal to 9cm, width equal to
8cm and volume equal to 168cm3.
A. 6cm
B. 7cm*
C. 8cm
D. 9cm
8. What is the formula in getting the surface area of a sphere?
A. V = 4/3Лr3*
B. V = 2/3Лr3
C. V = 3/4Лr3
D. V = 3/2Лr3
9. What is the volume of a cylinder having radius equal to 3cm and height equal to
10cm?
A. 282.744cm3*
B. 282.717cm3
C. 282.726cm3
D. 283.735cm3
10. What is the volume of a sphere having radius equal to 0.9m?
A. 3.0535m3
B. 3.0536m3*
C. 3.0537m3
D. 3.0534m3

14. Matching Type
Directions: Match column A with column B. Write only the letter with the correct
answer.
Column A Column B
1. Amount of space outside the sphere
2. Amount of space enclosed in a
rectangular prism
3. Amount of space enclosed in a
cone
4. Amount of space enclosed in
sphere
5. Amount of space outside the
rectangular prism
6. Amount of space outside the
cylinder
7. Amount of space enclosed in a
cylinder
8. Amount of space enclosed in a
square pyramid
9. Amount of space outside the cube
10. Amount of space outside the cone
a. SA = 2B + LA
b. V = 4/3 Лr3
c. V = 1/3 Лr2h
d. V = l x w x h
e. SA = 4Лr2
f. SA = Лr2 + Лrs
g. SA = 6s2
h. V = 1/3 (l x w) h
i. V = Лr2h
j. SA = 2Лr2 + 2Лrh
k. SA = s2 + 2bs
l. V = bh/2 x H