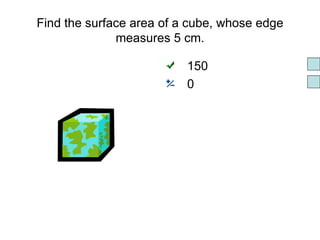
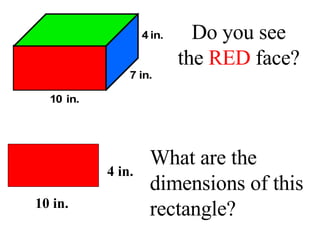
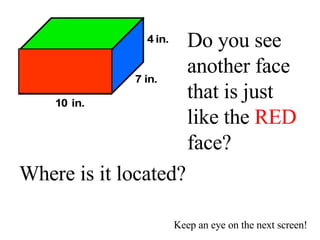
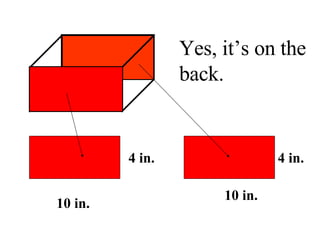
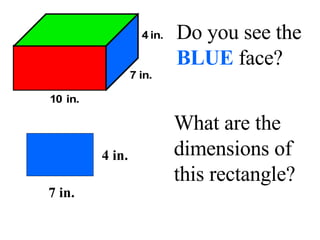
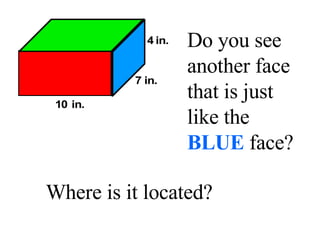
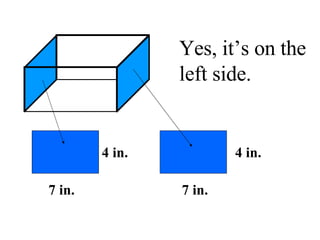
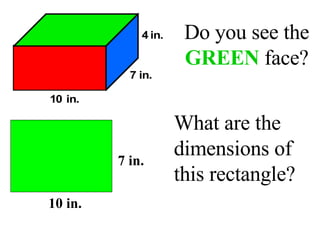
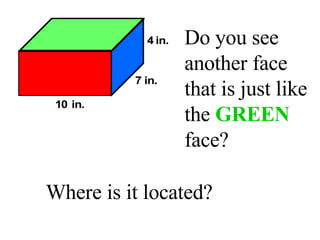
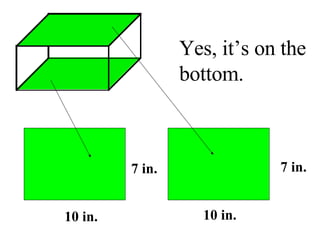
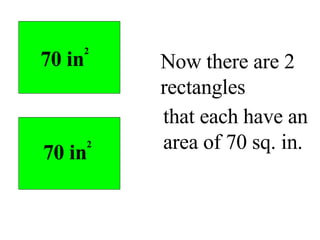
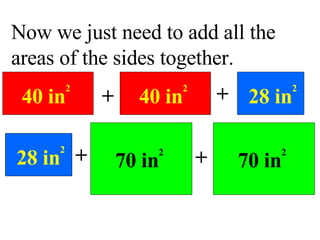
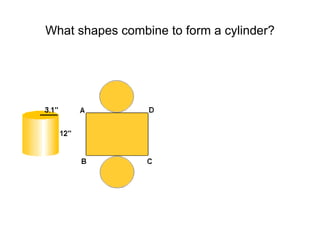
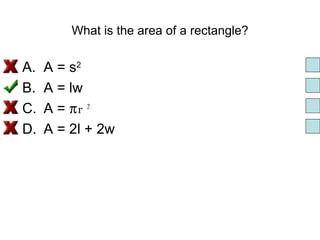Surface area is the total area of the outer surface of an object. To find the surface area, you break the object down into its component shapes and add the areas of each shape. For a cube, the surface area formula is SA = 6s^2, where s is the length of one edge. For a rectangular prism, the surface area formula is SA = 2lw + 2wh + 2lh, where l is length, w is width, and h is height. For a cylinder, the surface area formula is SA = 2πr^2 + 2πrh, where r is the radius and h is the height.

1. Surface Area of Solids

2. What is surface area? Consider the cylinder shown in the picture. What two dimensional shapes combine to form the cylinder?

3. What is surface area? Surface area is the material it takes to create the object. Think of taking apart the object piece by piece and finding the area of each piece (shape). Add the areas of the shapes that form the object to get the surface area.

4. What shapes combine to form a cube? circles rectangles Rectangles and squares squares

5. How do we find area of a square? A = lw A = bh A = s 2 A = π r 2

6. How many squares combine to form a cube? (Each one is called a “face.”) 4 6 8 10

7. What is the formula for the surface area of a cube? SA = s 2 SA = 6s 2 SA = s 3 SA = 6s 3

8. Find the surface area of a cube, whose edge measures 5 cm. 150 0

9. What shapes combine to form a rectangular prism (box)?

10. What shapes combine to form a rectangular prism (box)? Circles and squares Squares Squares and rectangles Rectangles

11. What is the area of a rectangle? A = s 2 A = lw A = πr 2 A = 2l + 2w

12. How many rectangles form a rectangular prism? 6 0

13. Let’s look at a rectangular prism

14. Do you see the RED face? What are the dimensions of this rectangle? 10 in. 4 in.

15. Do you see another face that is just like the RED face? Where is it located? Keep an eye on the next screen!

16. Yes, it’s on the back. 10 in. 4 in. 10 in. 4 in.

17. Now there are 2 rectangles that each have an area of 40 sq. in. 40 in 2 40 in 2

18. Do you see the BLUE face? What are the dimensions of this rectangle? 4 in. 7 in.

19. Do you see another face that is just like the BLUE face? Where is it located?

20. Yes, it’s on the left side. 4 in. 7 in. 7 in. 4 in.

21. Now there are 2 rectangles that each have an area of 28 sq. in. 28 in 2 28 in 2

22. Do you see the GREEN face? What are the dimensions of this rectangle? 10 in. 7 in.

23. Do you see another face that is just like the GREEN face? Where is it located?

24. Yes, it’s on the bottom. 10 in. 7 in. 10 in. 7 in.

25. Now there are 2 rectangles that each have an area of 70 sq. in. 70 in 2 70 in 2

26. Now we just need to add all the areas of the sides together. + + + + 70 in 2 28 in 2 40 in 2 40 in 2 28 in 2 70 in 2

27. The total Surface Area for this rectangular prism is 40 + 40 + 28 + 28 + 70 + 70 = 276 in 2

28. Based on the previous example what is the formula for the surface area of a rectangular prism? SA = 6lw SA = lw + wh + lh SA = 2lw + 2wh + 2lh SA = lwh

29. Use the formula to find the surface area of the rectangular prism with l = 6, w = 5 and b = 4. 148 0

30. What shapes combine to form a cylinder?

31. What shapes combine to form a cylinder?

32. What shapes combine to form a cylinder? circles rectangles Circles and rectangle Square and circles

33. What formula can be used to find the surface area of a cylinder? SA = πr 2 SA = 2 πr 2 + πdh SA = πr 2 h SA = 2 πr 2 + lw

34. Find the surface area of a cylinder whose radius is 5 and whose height is 8. (to the nearest tenth) 408.4 0

35. Basically, surface area can be found by ADDING THE AREAS OF THE INDIVIDUAL SURFACES (SHAPES) THAT ARE COMBINED TO FORM THE OBJECT.