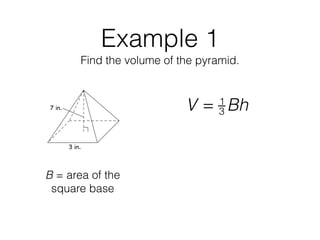
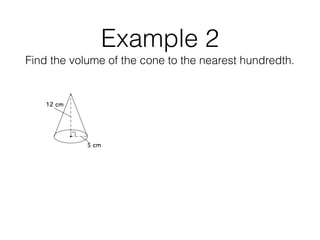
This document discusses how to calculate the volumes of pyramids and cones. It provides the formulas for volume of a pyramid (V=1/3Bh) and volume of a cone (V=1/3πr^2h) and works through multiple examples of applying the formulas. It finds the volumes of various pyramids and cones by plugging dimensions like base area, height, radius, etc. into the appropriate volume formula.