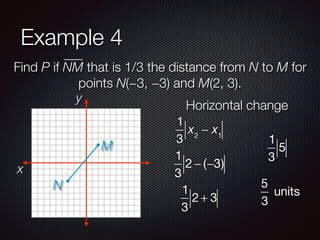
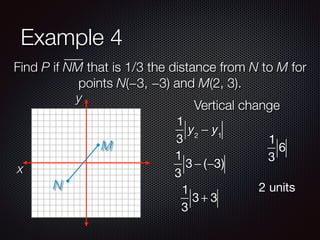
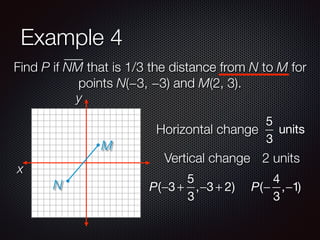
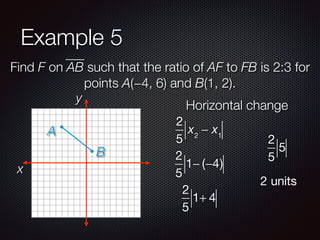
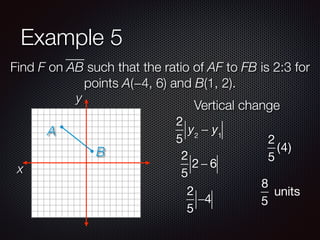
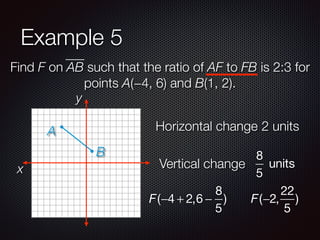
This document discusses finding points and midpoints on line segments. It defines midpoint as the point halfway between two endpoints and provides the formula to calculate it. Several examples are given to demonstrate how to find the midpoint of a segment, locate a point at a fractional distance from one endpoint, and find a point where the ratio of distances from the endpoints is a given ratio. The key concepts covered are calculating midpoints using averages of x- and y-coordinates, and setting up and solving equations to locate interior points using fractional or ratio distances along a segment.

1. Section 1-3
Locating Points and Midpoints

2. Essential Questions
How do you find the midpoint of a segment?
How do you locate a point on a segment given a
fractional distance from one endpoint?

3. Vocabulary
1. Midpoint: The point on a segment that is halfway
between the endpoints
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ for (x1
,y1
) and (x2
,y2
)
2. Segment Bisector: Any segment, line, or plane
that intersects another segment at its midpoint

4. Example 1
Find the midpoint of AB for points A(3, 2) and
B(6, 8).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ =
3 + 6
2
,
2 + 8
2
⎛
⎝⎜
⎞
⎠⎟
=
9
2
,
10
2
⎛
⎝⎜
⎞
⎠⎟ =
9
2
,5
⎛
⎝⎜
⎞
⎠⎟ or 4.5,5( )

5. Example 2
Find the coordinates of U if F(−2, 3) is the
midpoint of UO and O has coordinates of (8, 6).
M =
x1
+ x2
2
,
y1
+ y2
2
⎛
⎝
⎜
⎞
⎠
⎟ (−2,3) =
x + 8
2
,
y + 6
2
⎛
⎝⎜
⎞
⎠⎟
−2 =
x + 8
2
i2(2)i ( )
−4 = x + 8
x = −12
3 =
y + 6
2
i22i
6 = y + 6
y = 0
U(−12,0)

6. Example 3
Find PQ if Q is the midpoint of PR.
2x + 3 4x − 1
P Q R
2x + 3 = 4x − 1
4 = 2x
x = 2
PQ = 2x + 3
PQ = 2(2) + 3
PQ = 4 + 3
PQ = 7 units

7. Example 4
Find P if NM that is 1/3 the distance from N to M for
points N(−3, −3) and M(2, 3).
Horizontal change
1
3
x2
− x1
1
3
2 − (−3)
1
3
2 + 3
1
3
5
5
3
units
x
y
M
N

8. Example 4
Find P if NM that is 1/3 the distance from N to M for
points N(−3, −3) and M(2, 3).
Vertical change
1
3
y2
− y1
1
3
3 − (−3)
1
3
3 + 3
1
3
6
2 units
x
y
M
N

9. Example 4
Find P if NM that is 1/3 the distance from N to M for
points N(−3, −3) and M(2, 3).
Vertical change 2 units
Horizontal change
5
3
units
P(−3 +
5
3
,−3 + 2) P(−
4
3
,−1)
x
y
M
N

10. Example 5
Find F on AB such that the ratio of AF to FB is 2:3 for
points A(−4, 6) and B(1, 2).
3:2 means 2 parts of AF and 3 parts of FB for a
total of five parts. To go from A to F, we use 2/5
of the total distance from A to B.

11. Example 5
Find F on AB such that the ratio of AF to FB is 2:3 for
points A(−4, 6) and B(1, 2).
x
y
B
A
Horizontal change
2
5
x2
− x1
2
5
1− (−4)
2
5
1+ 4
2
5
5
2 units

12. Example 5
Find F on AB such that the ratio of AF to FB is 2:3 for
points A(−4, 6) and B(1, 2).
x
y
B
A
Vertical change
2
5
y2
− y1
2
5
2 − 6
2
5
−4
2
5
(4)
8
5
units

13. Example 5
Find F on AB such that the ratio of AF to FB is 2:3 for
points A(−4, 6) and B(1, 2).
x
y
B
A Horizontal change 2 units
Vertical change
8
5
units
F(−4 + 2,6 −
8
5
) F(−2,
22
5
)