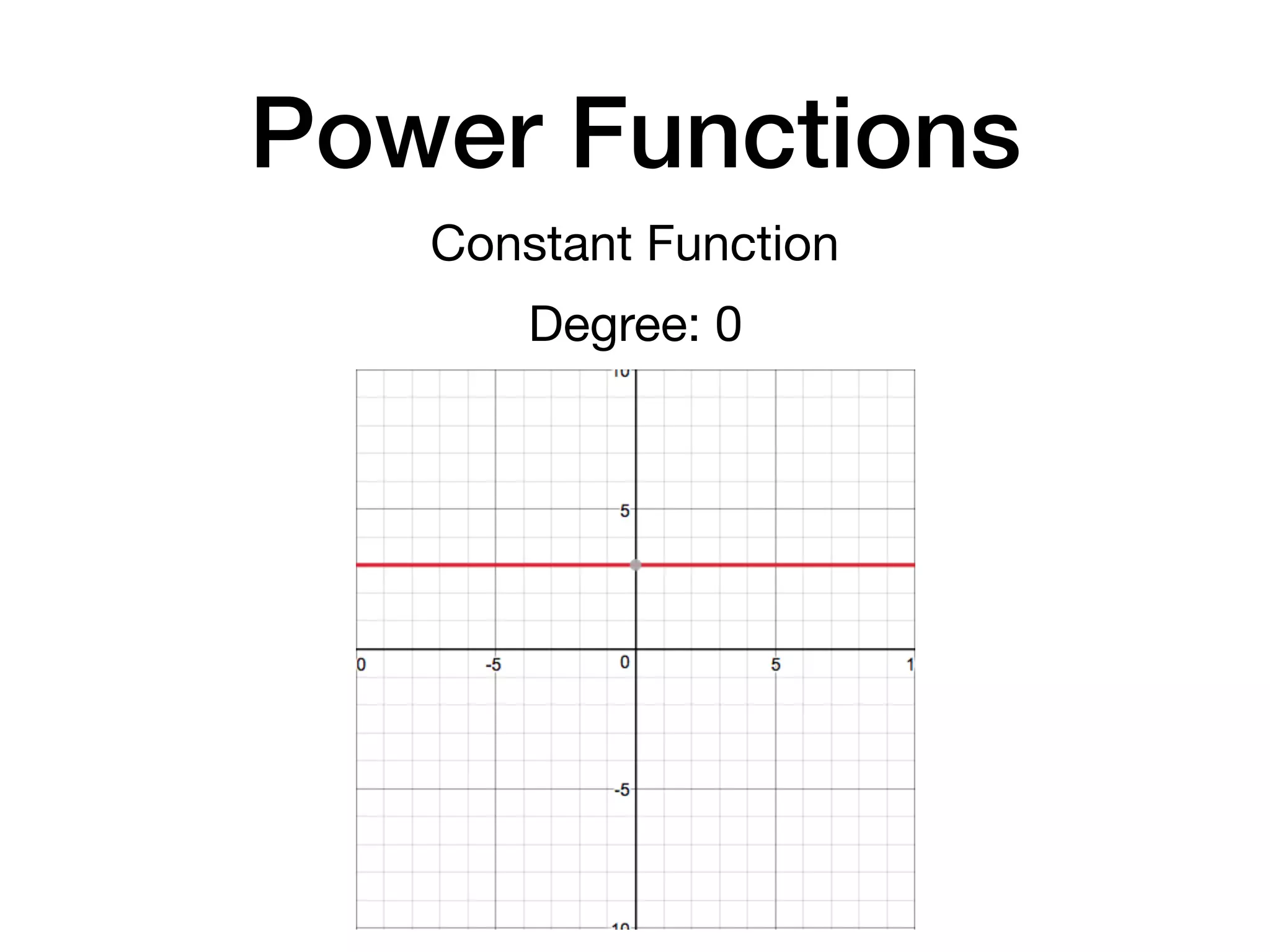
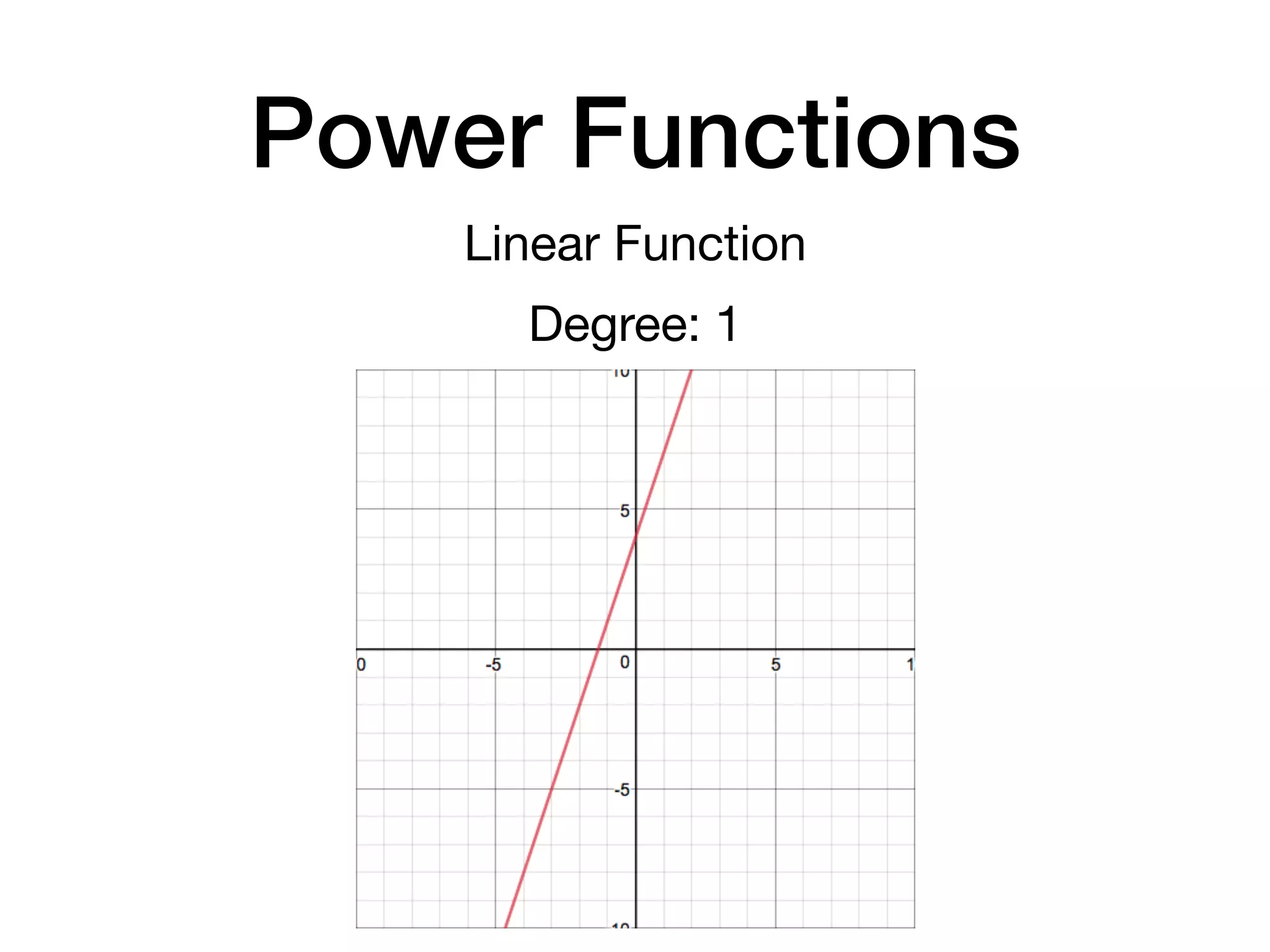
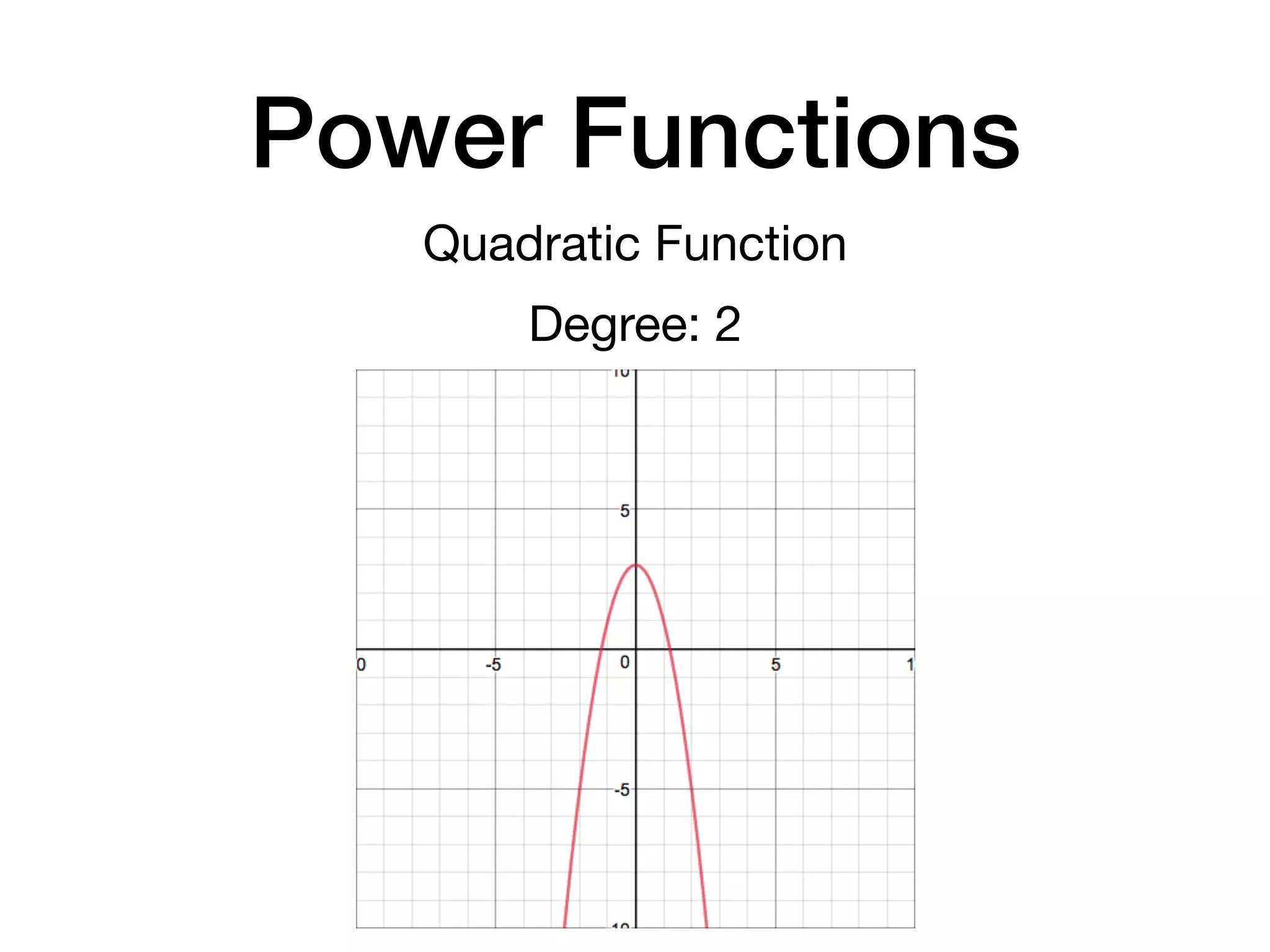
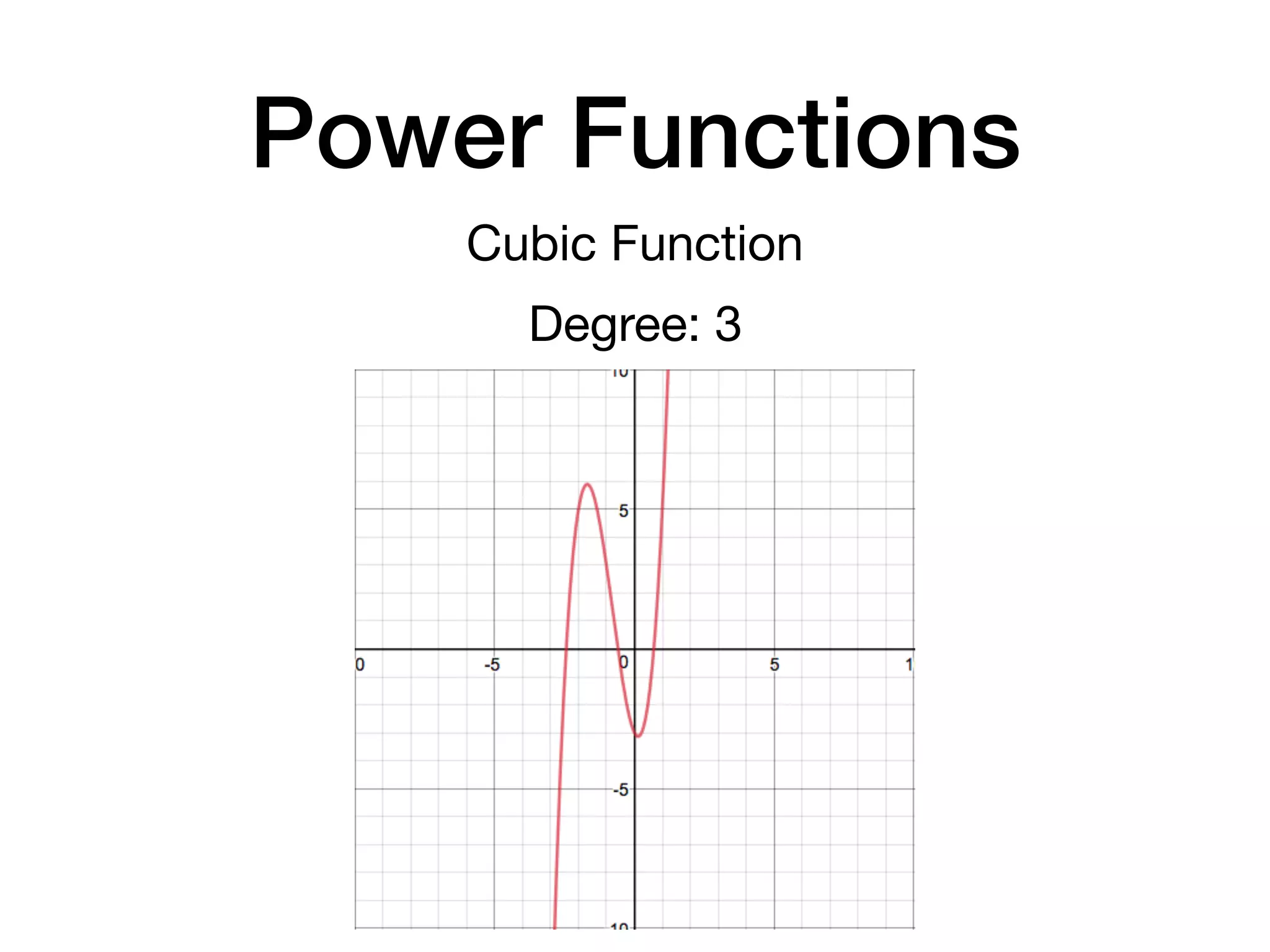
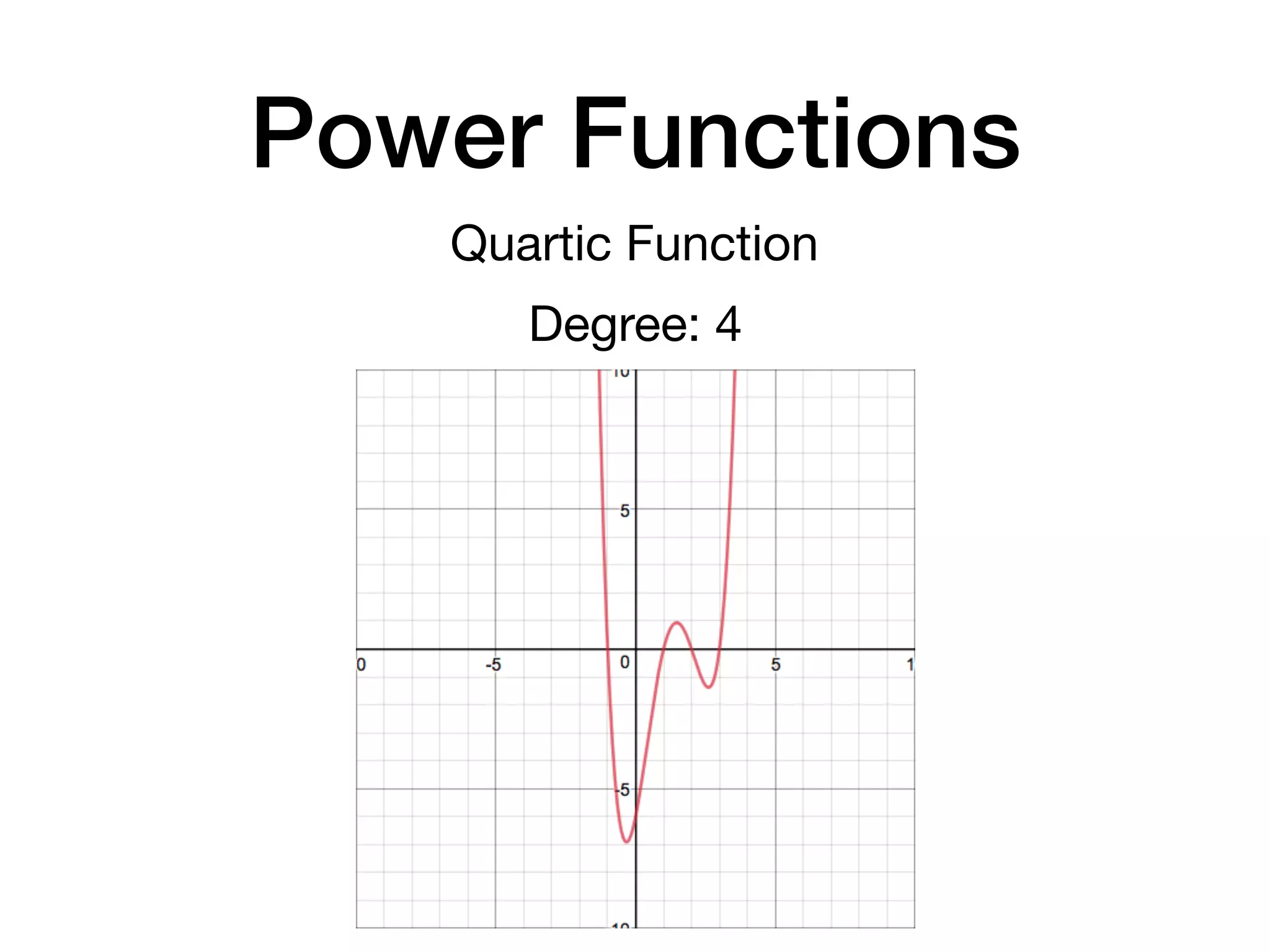
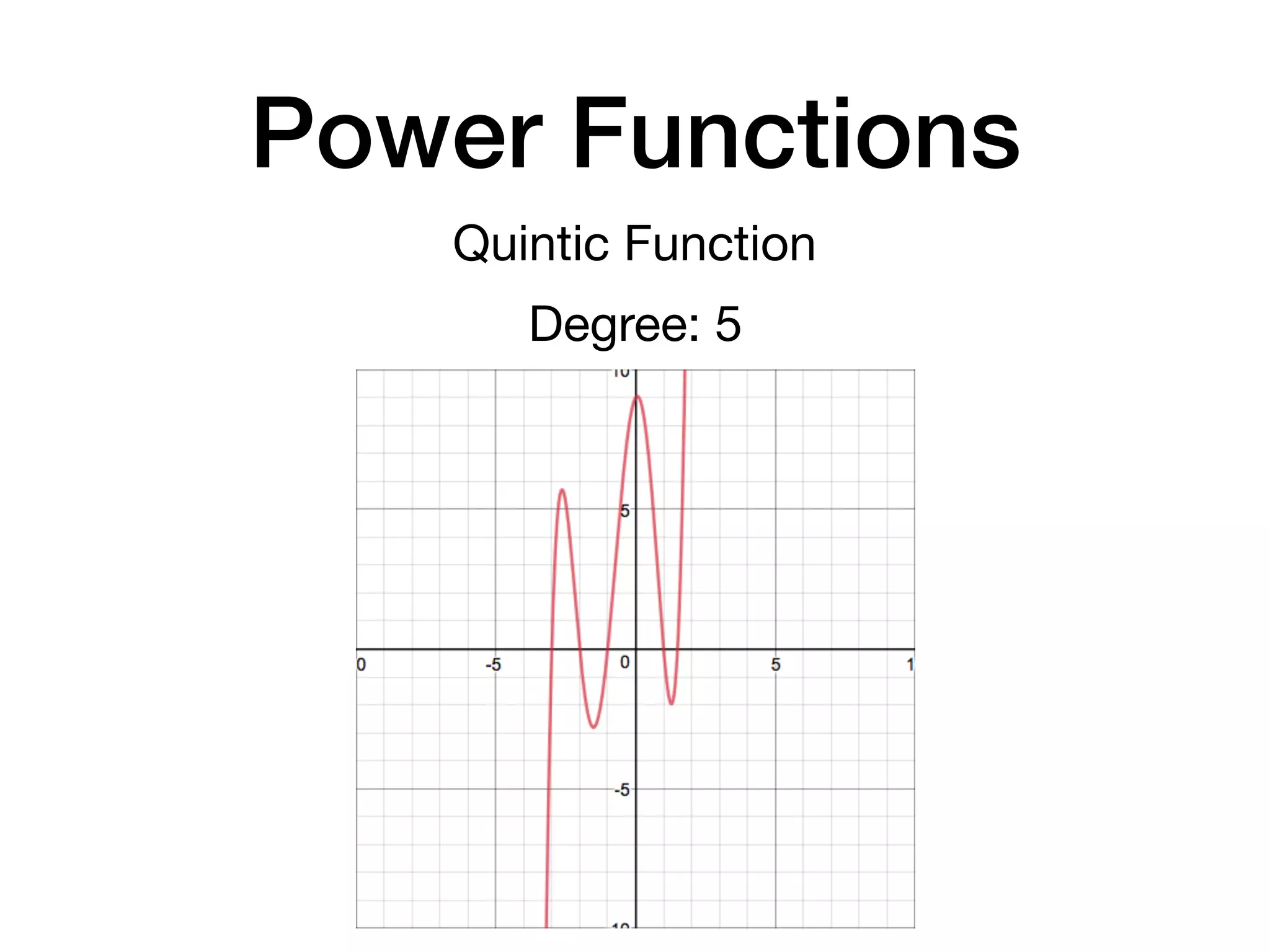
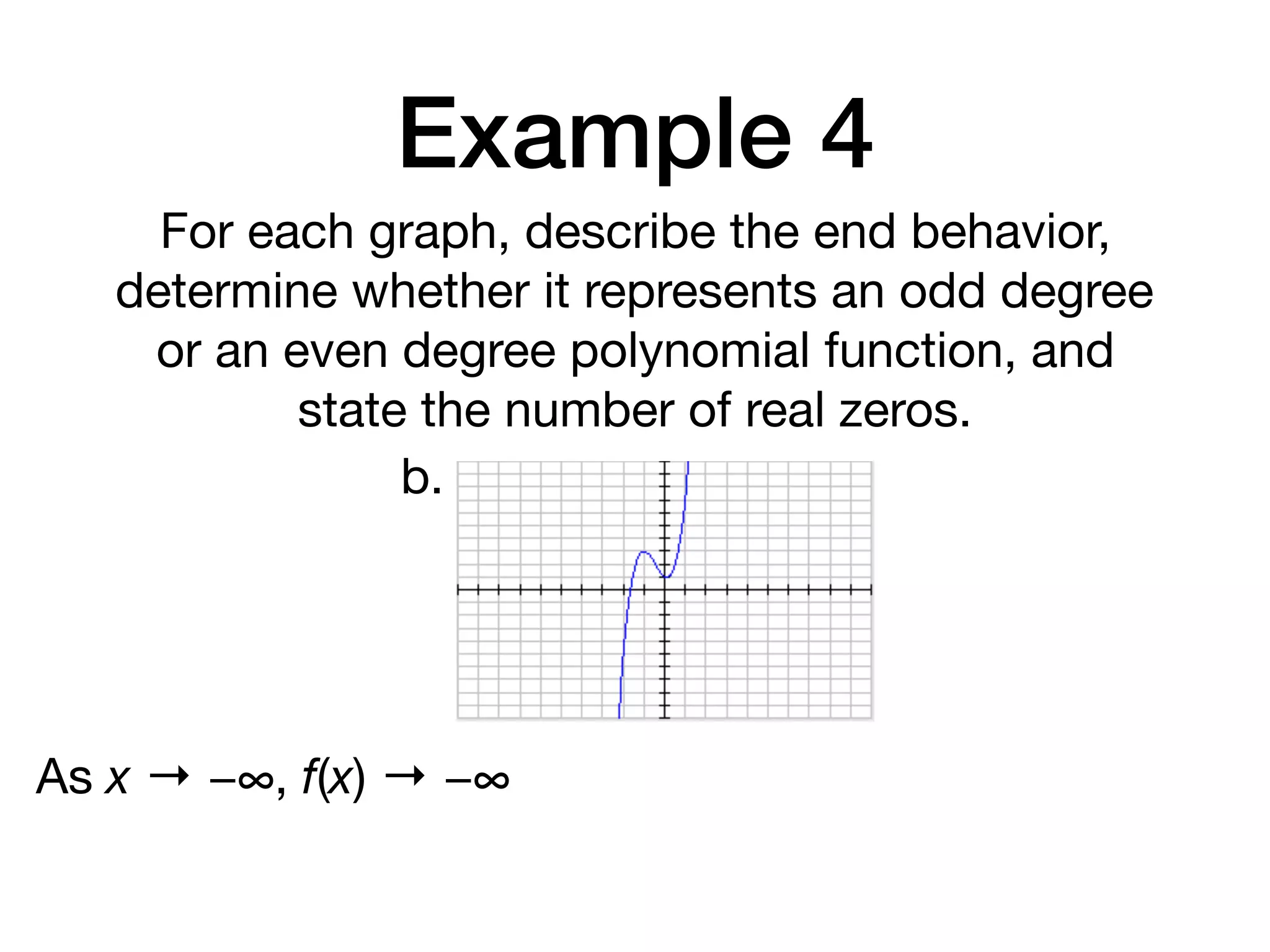
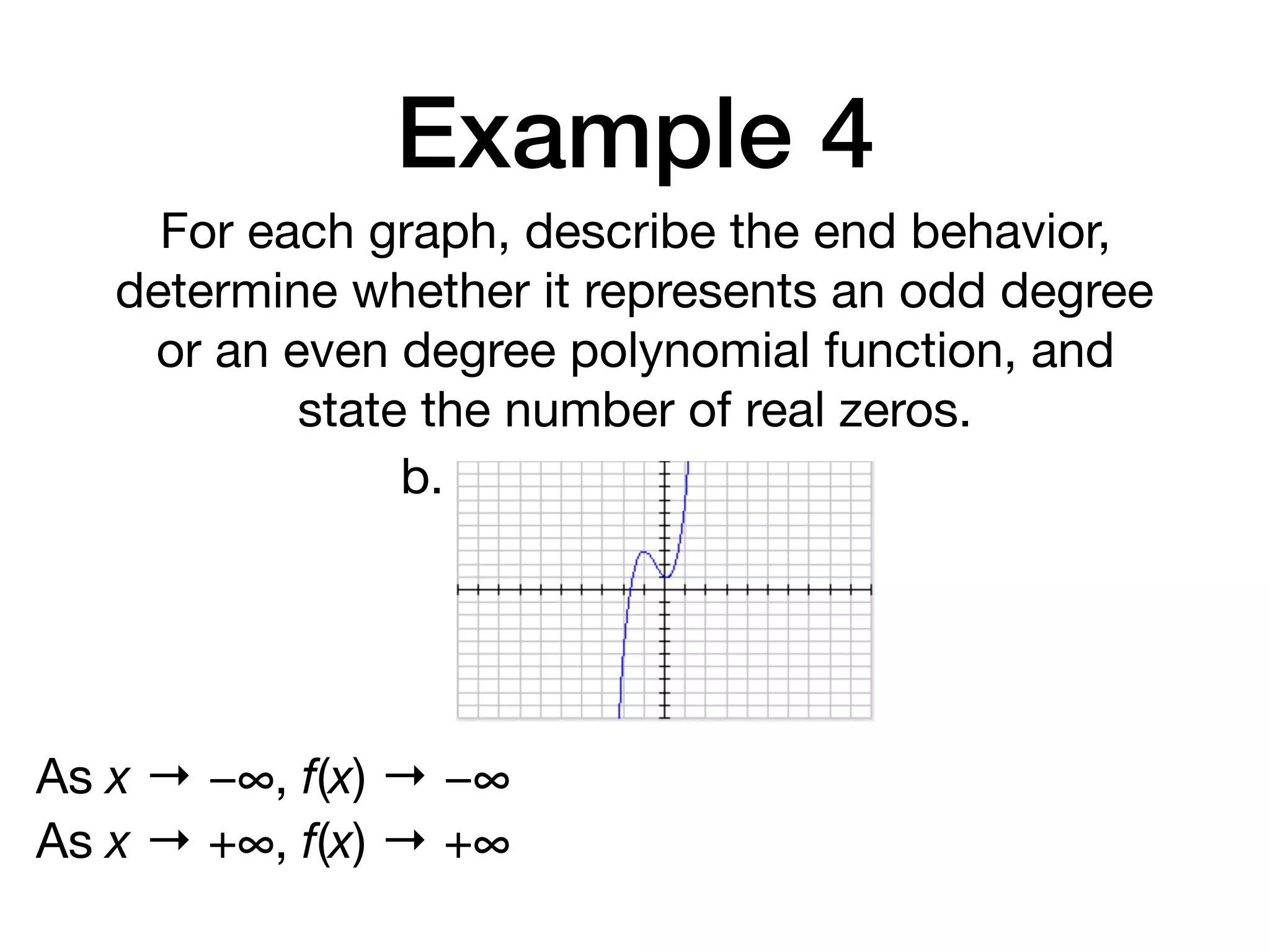
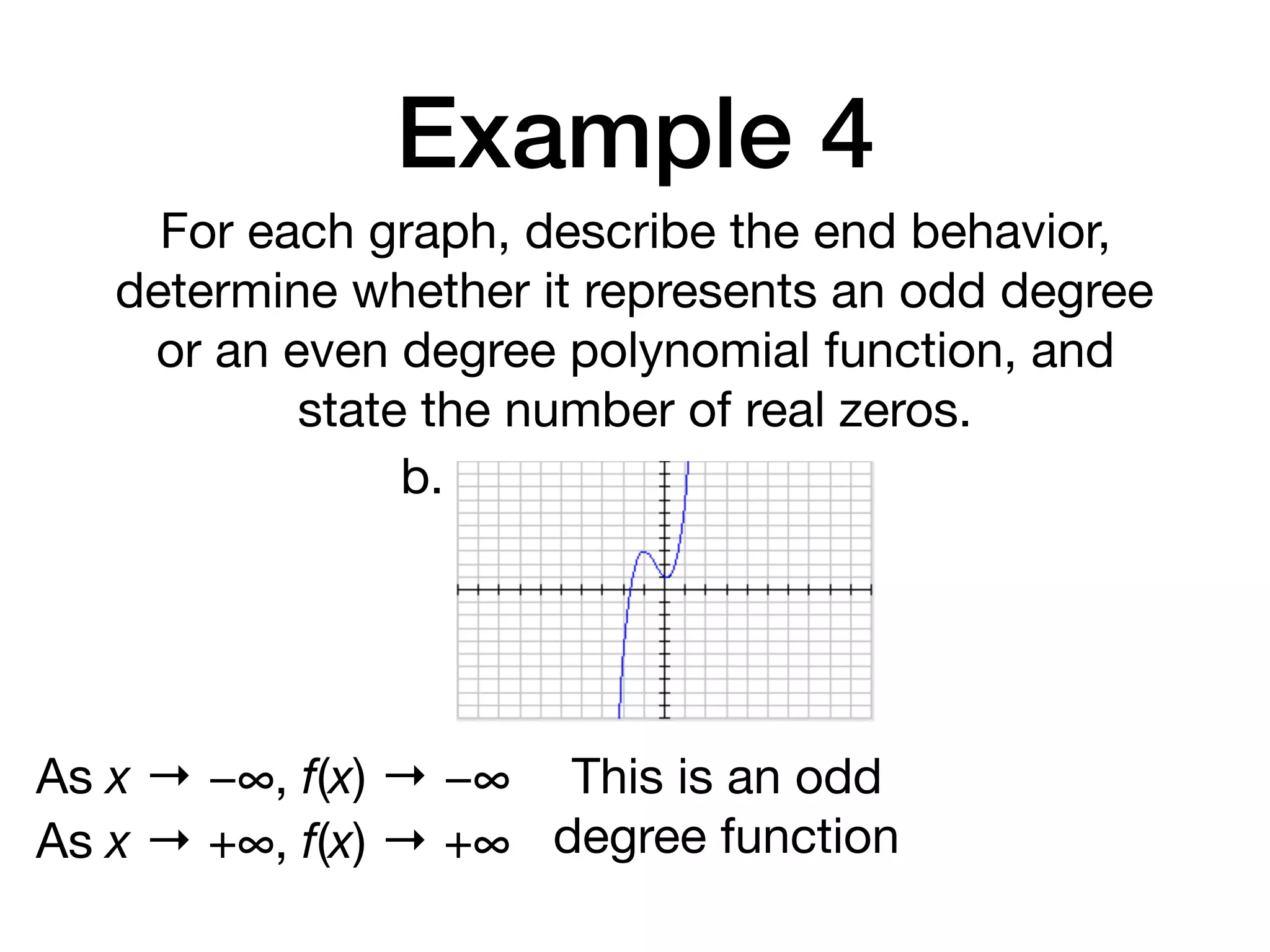
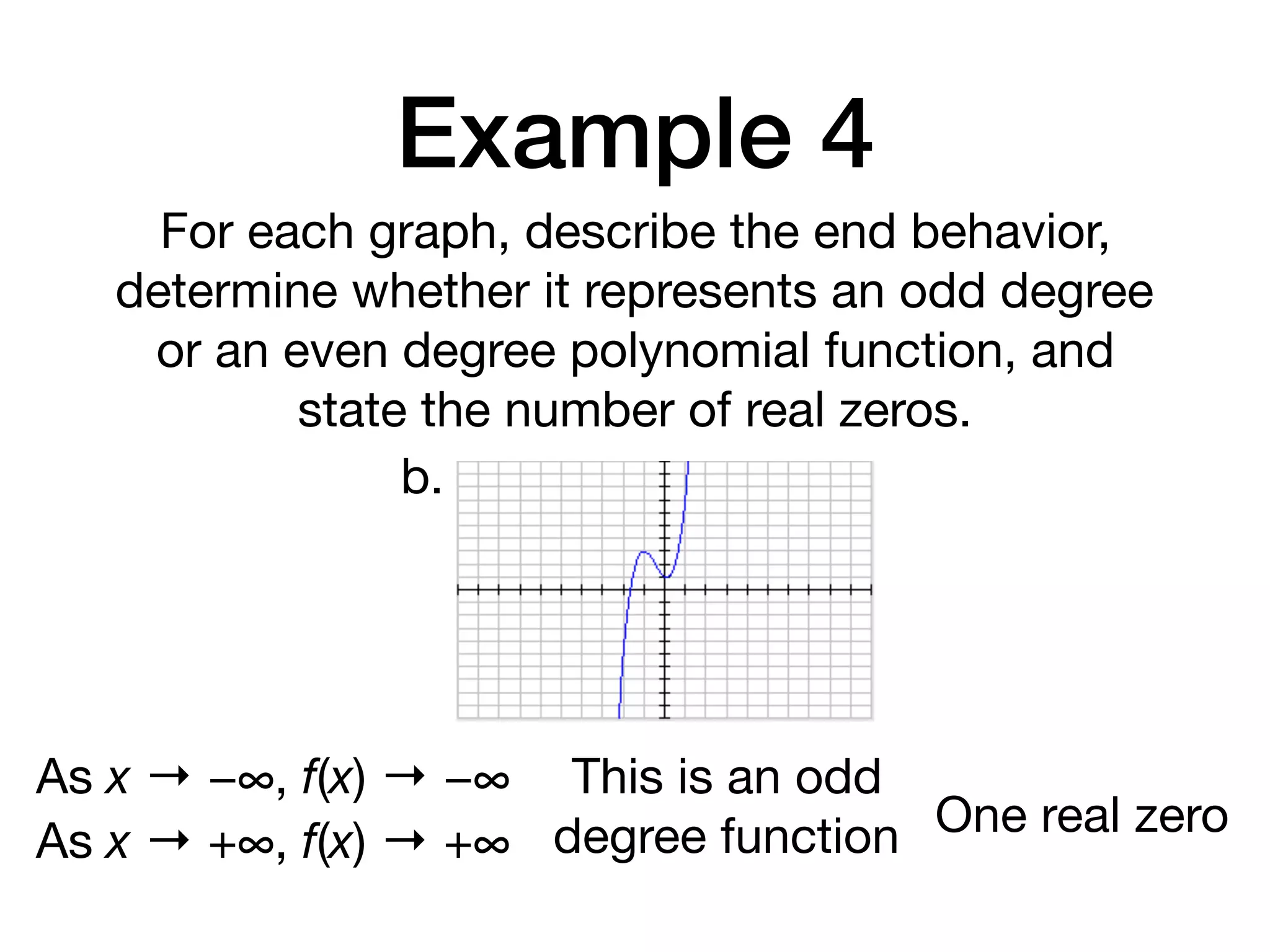
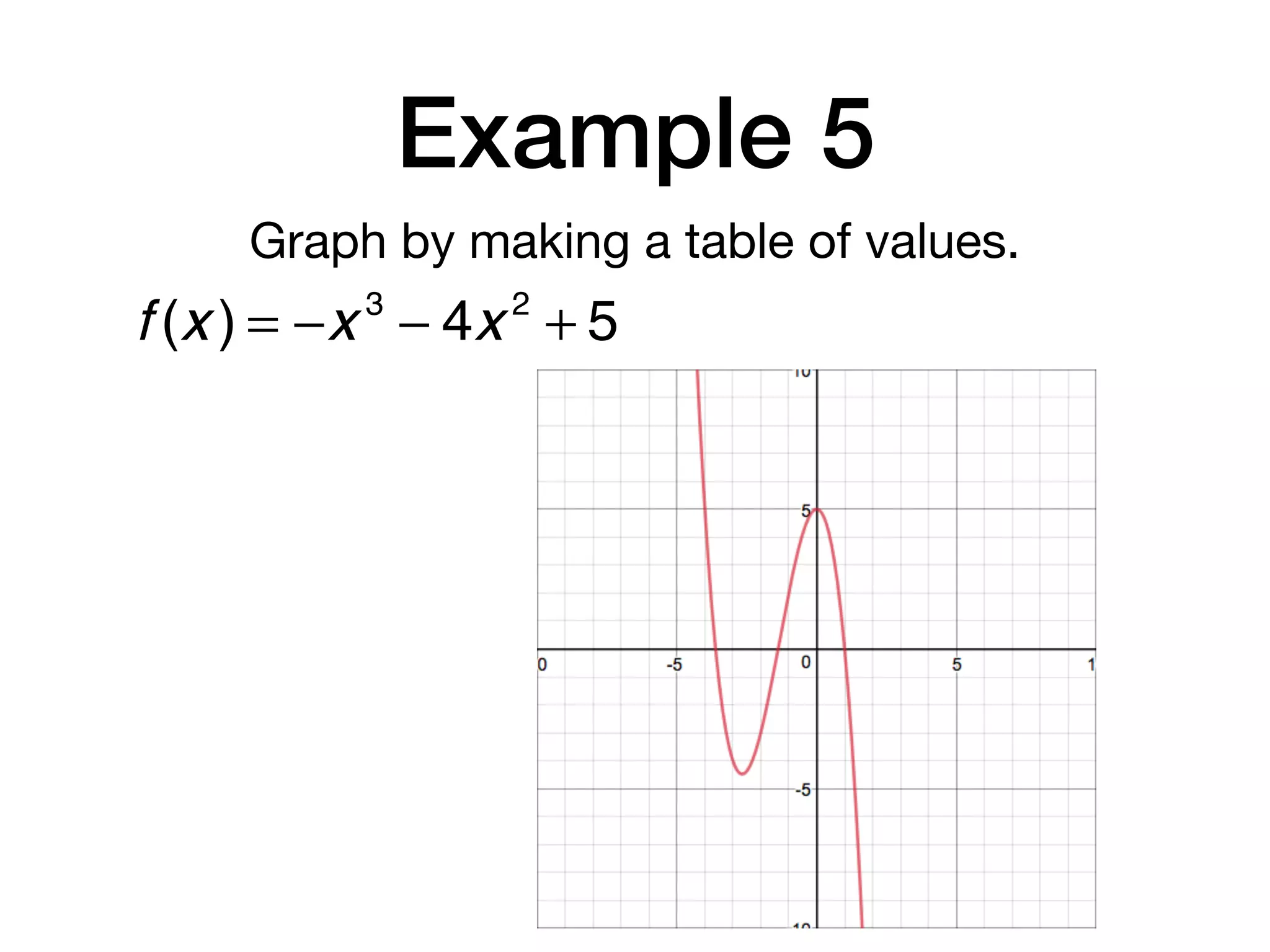
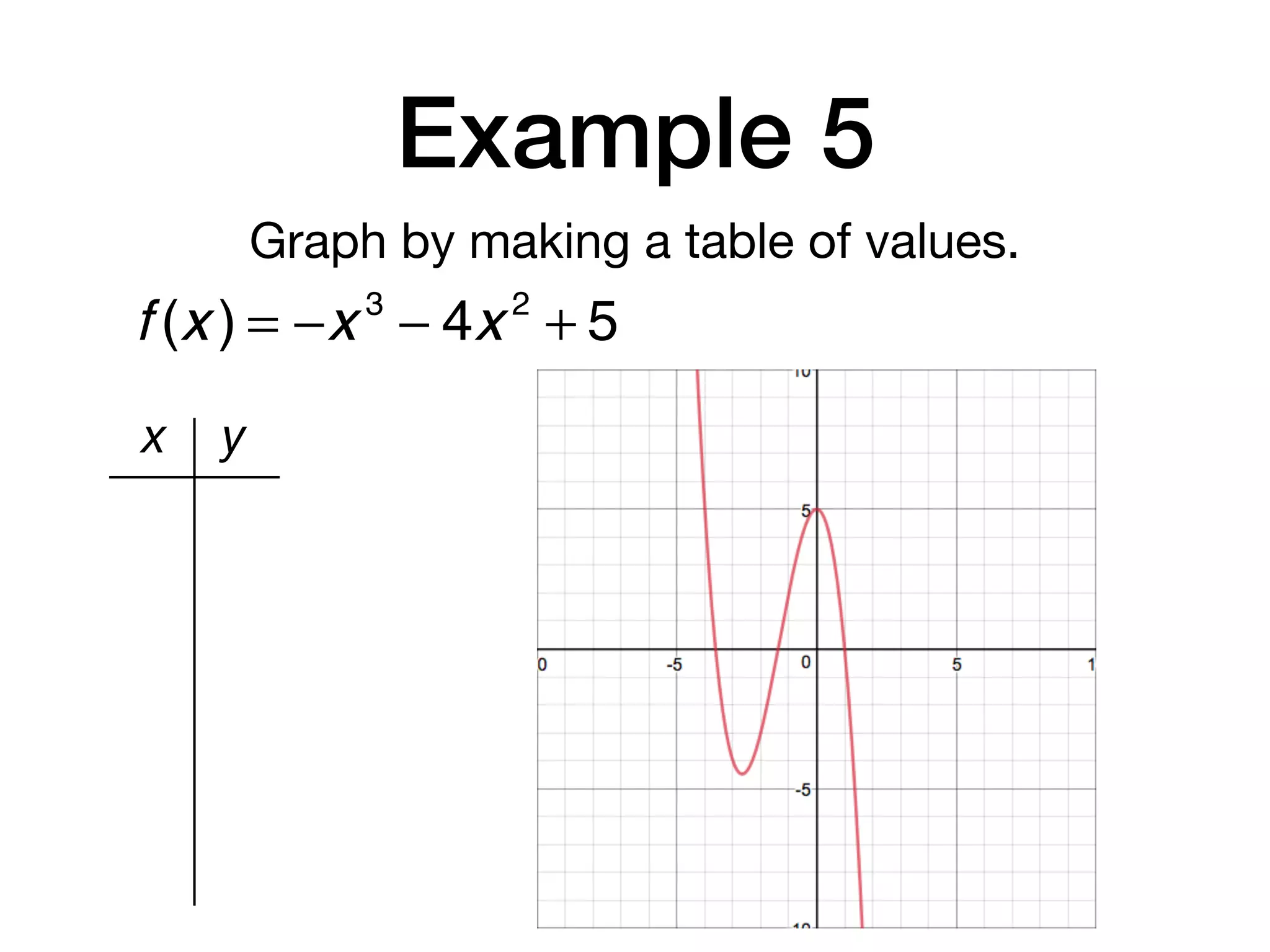
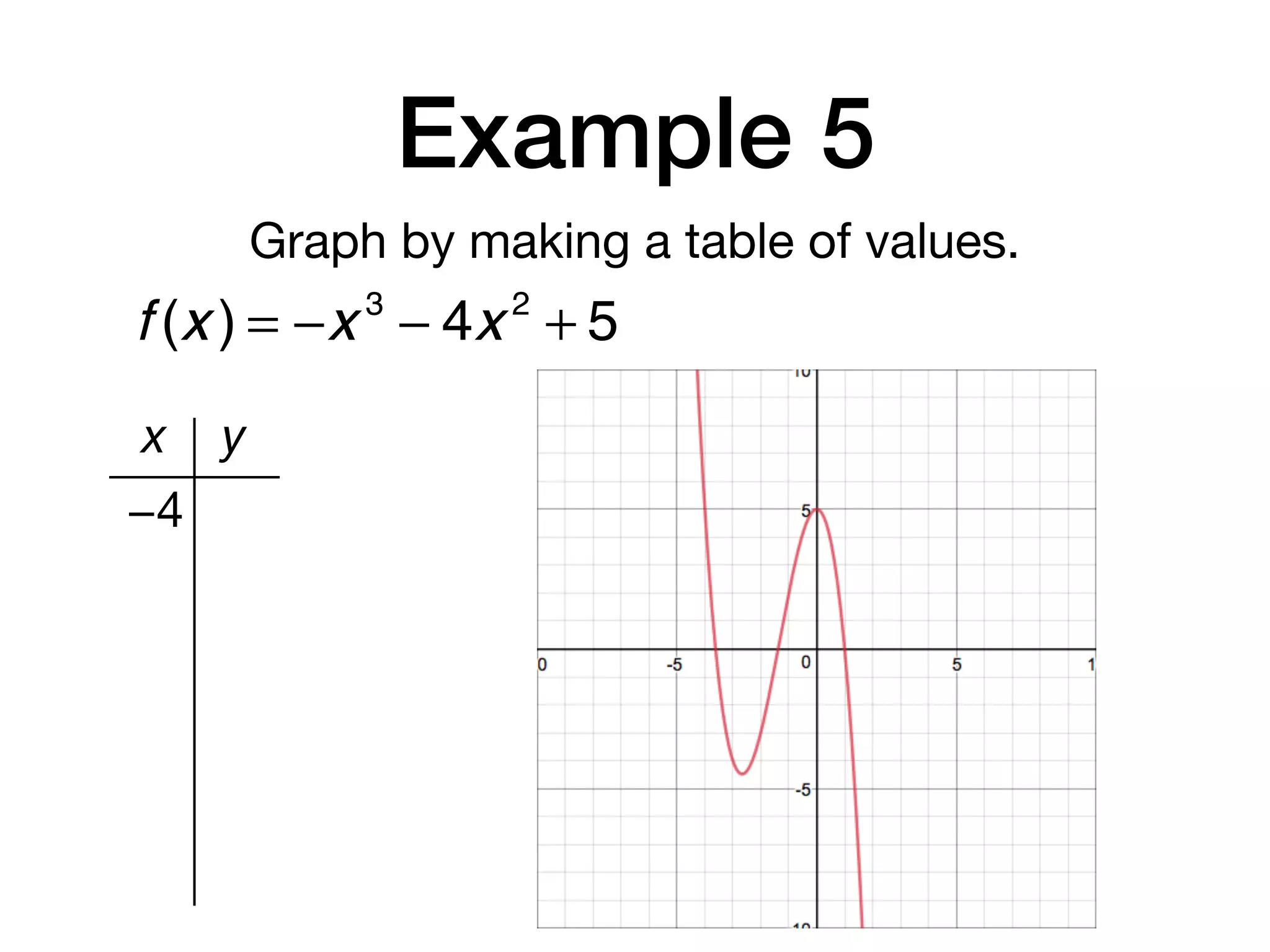
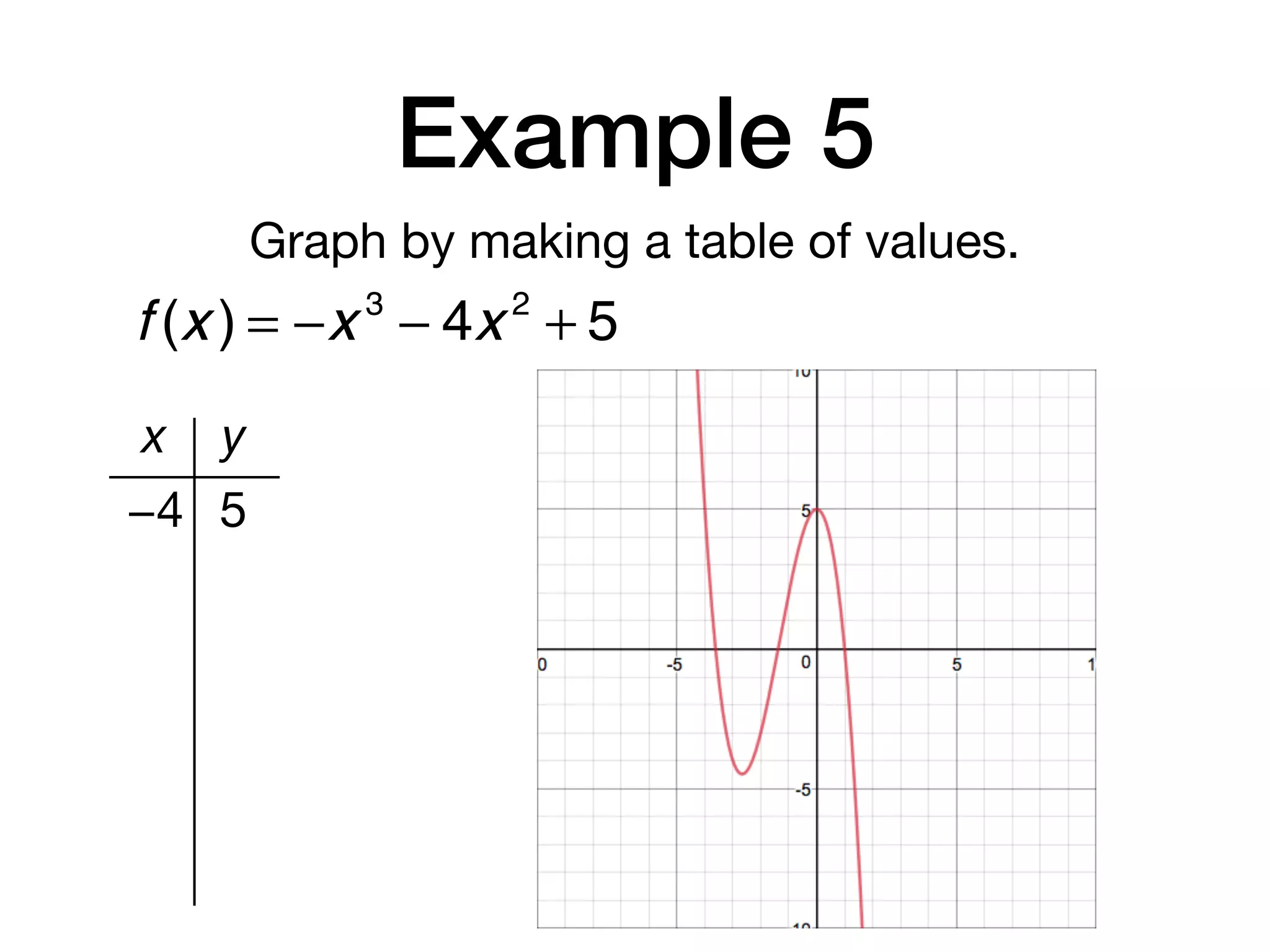
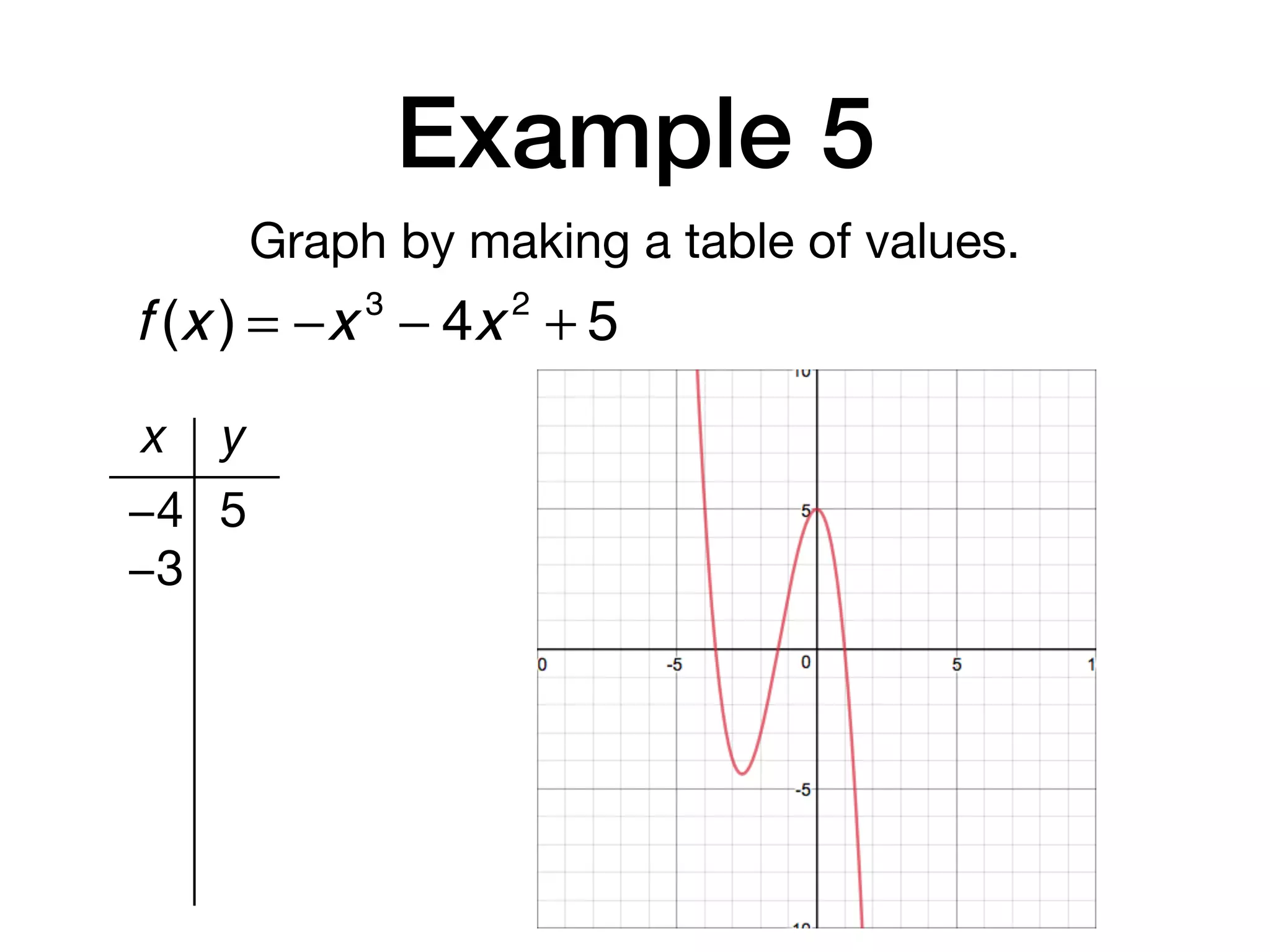
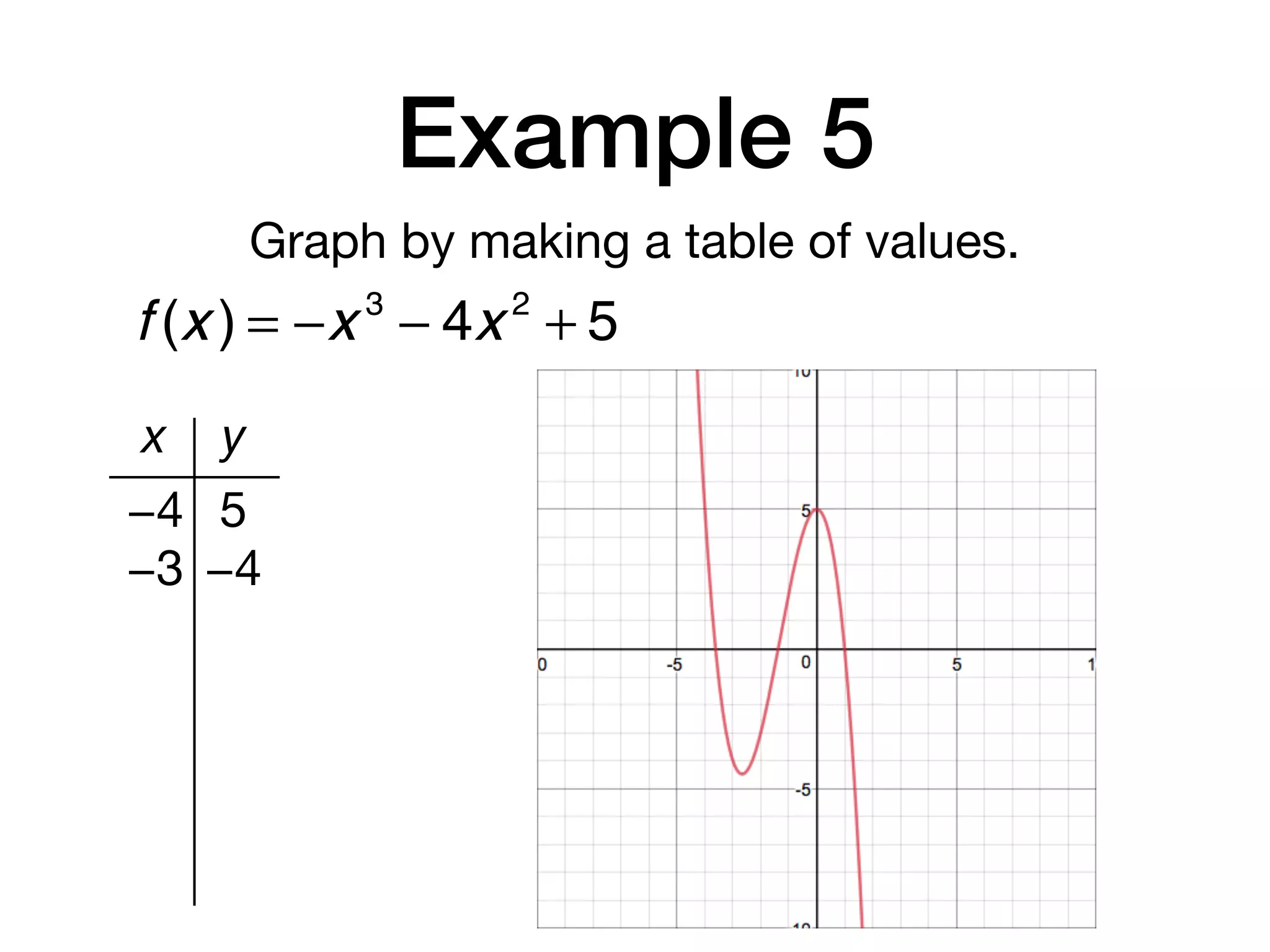
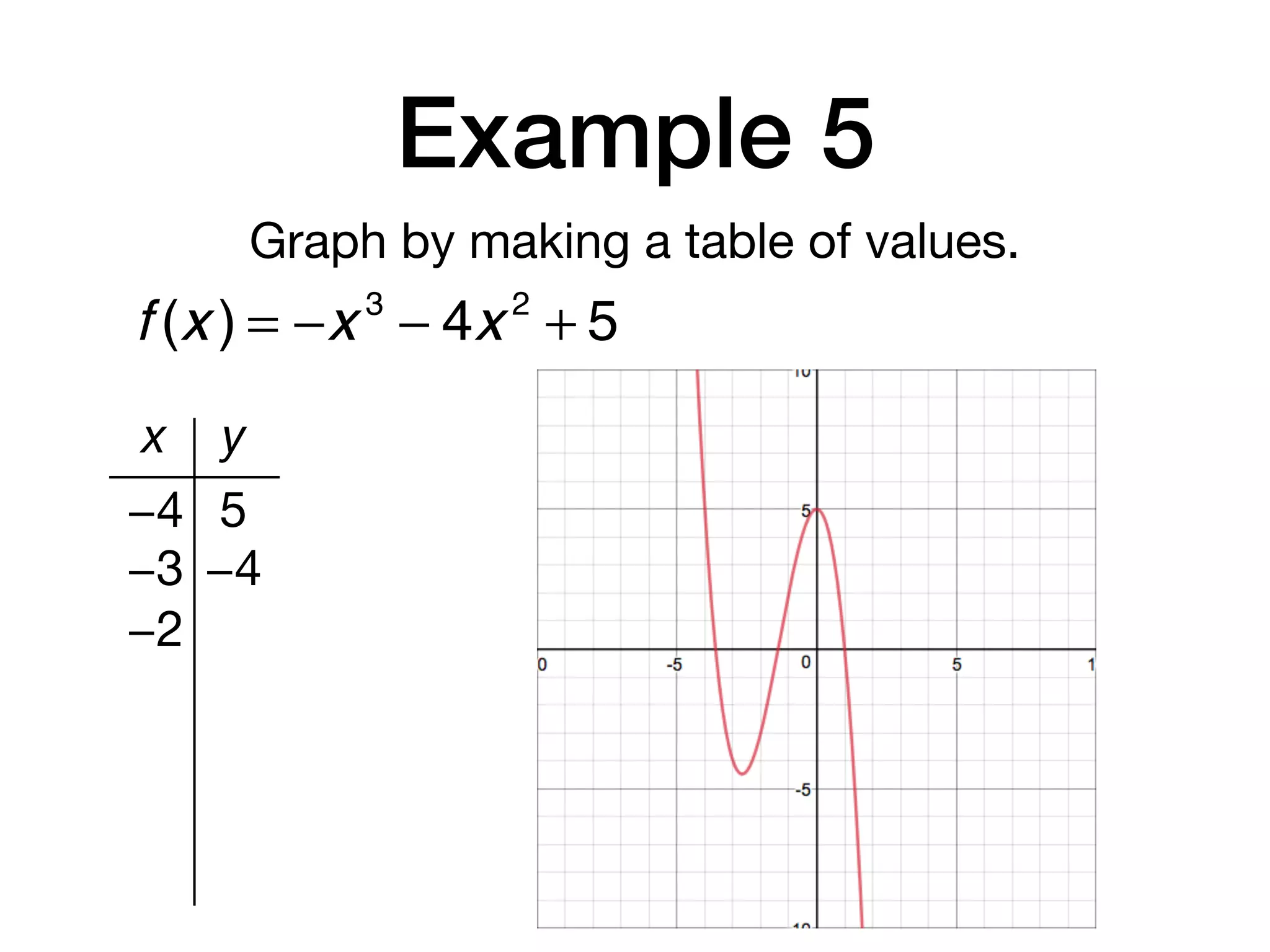
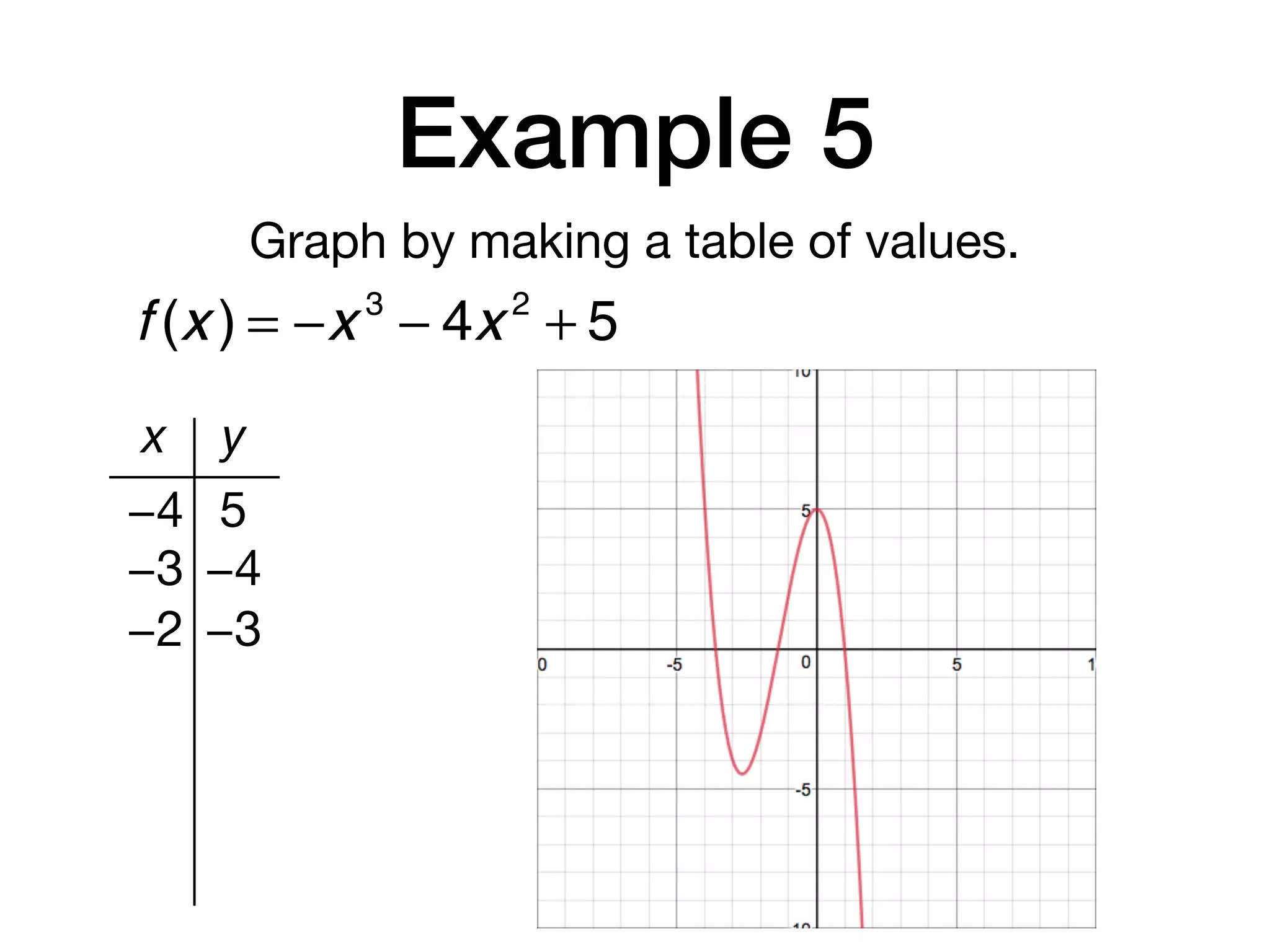
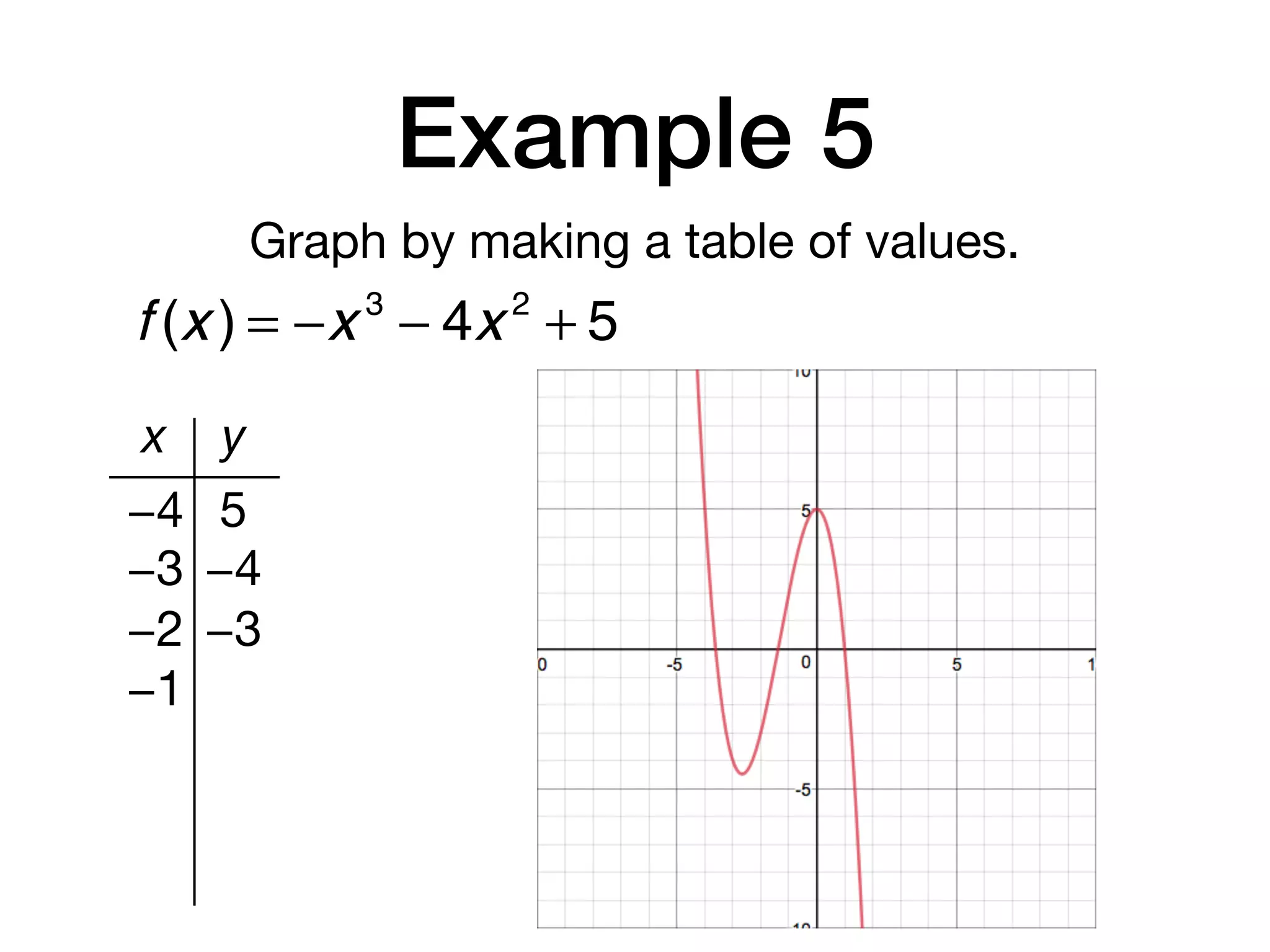
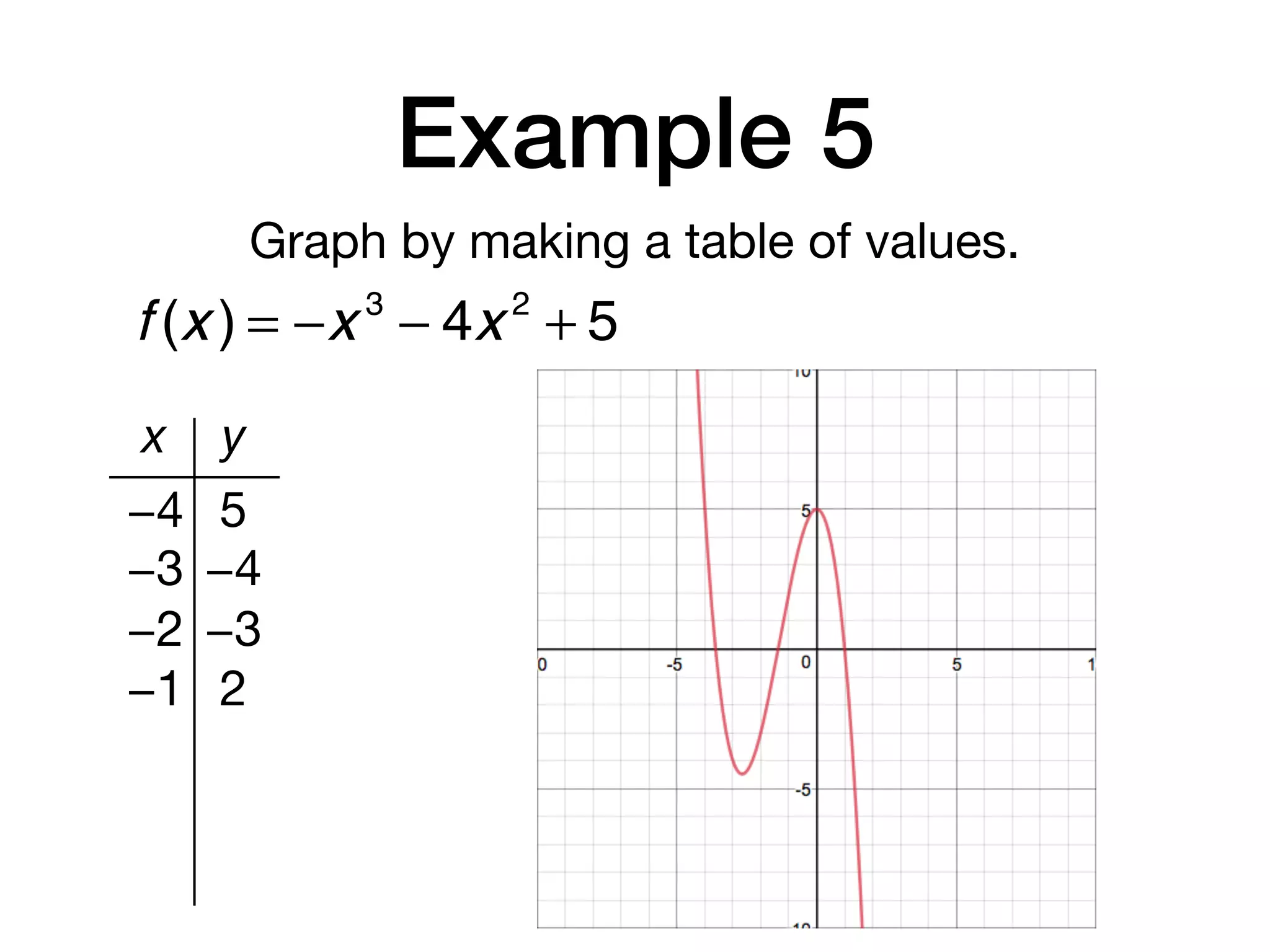
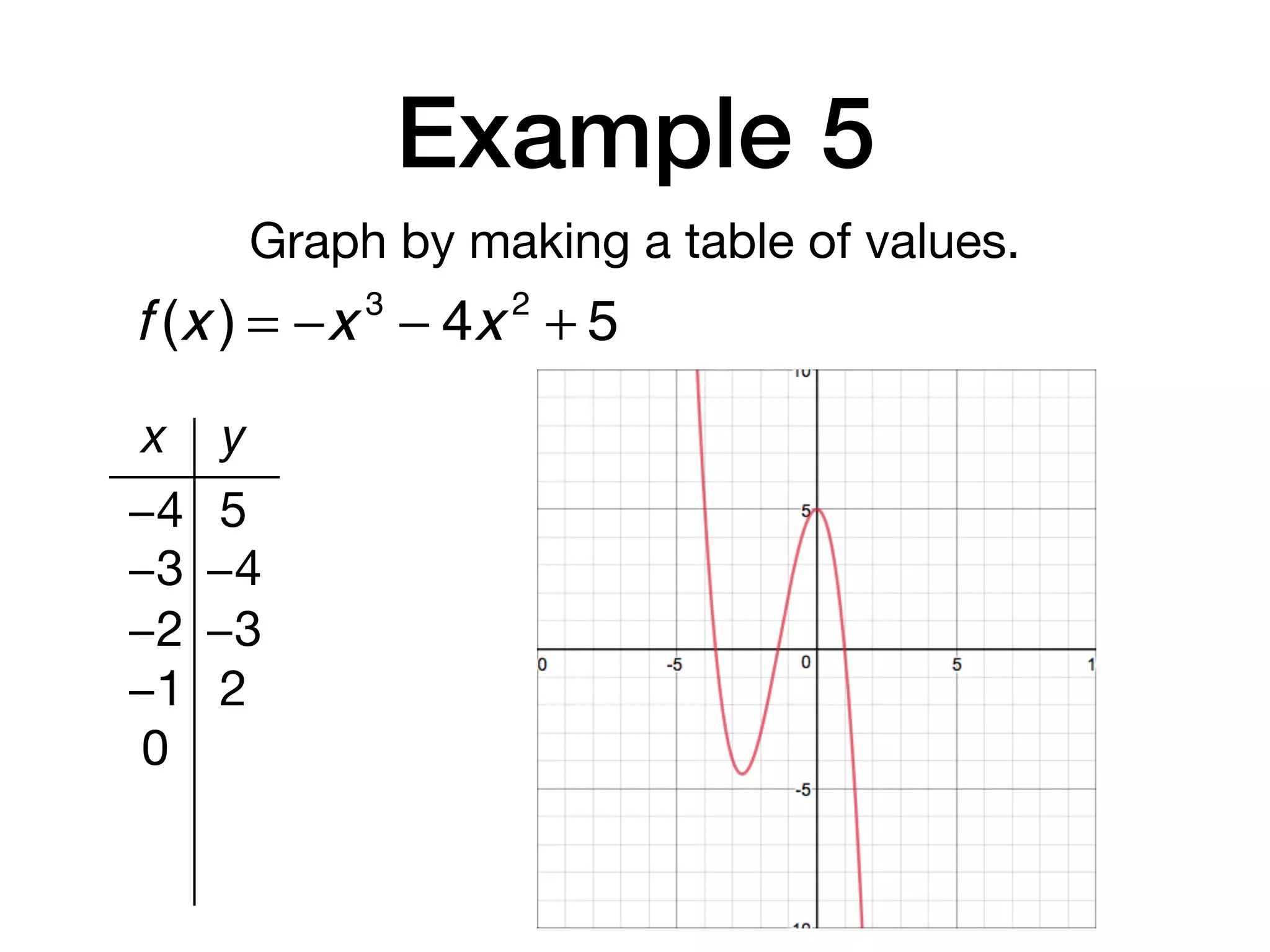
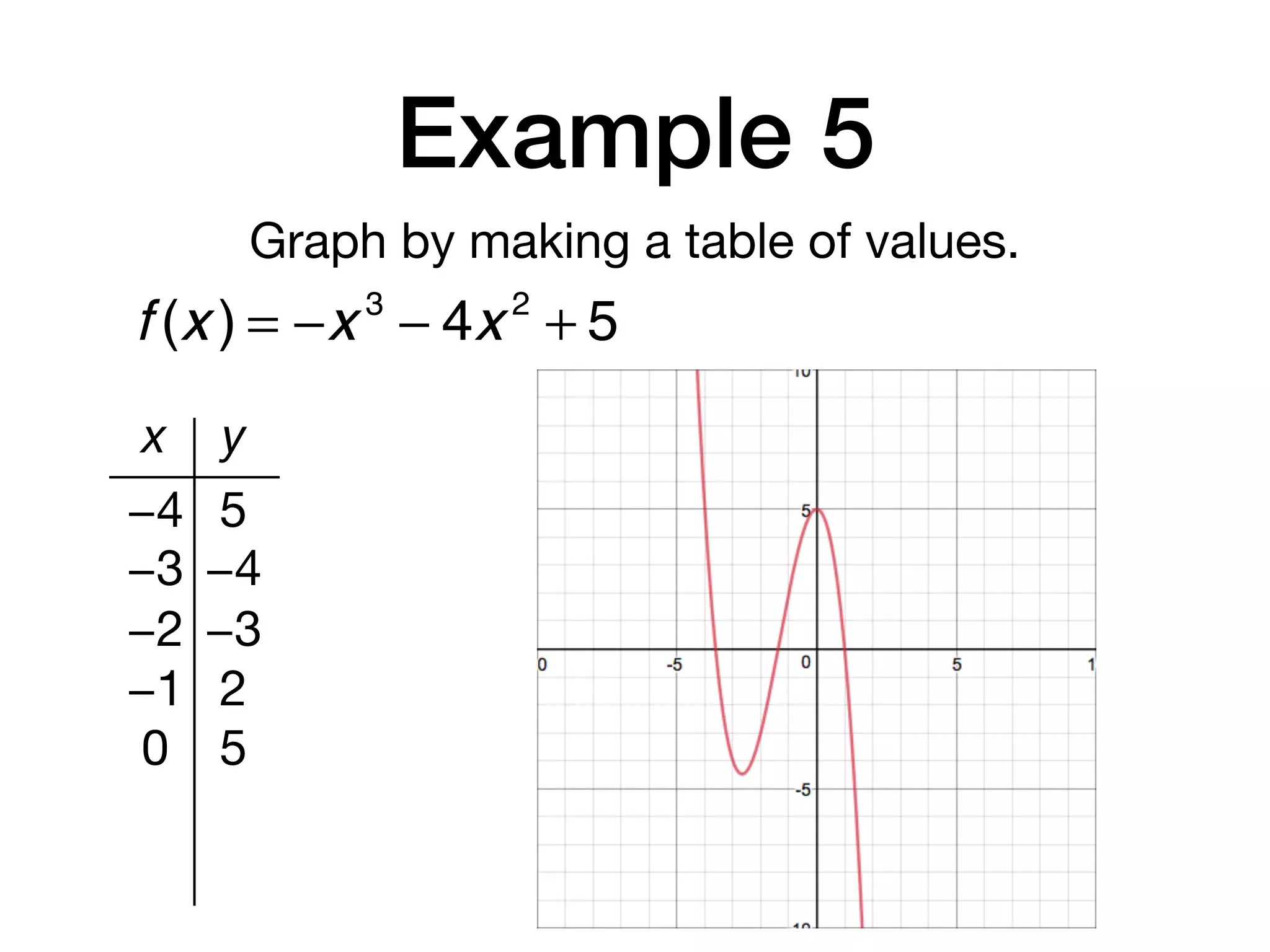
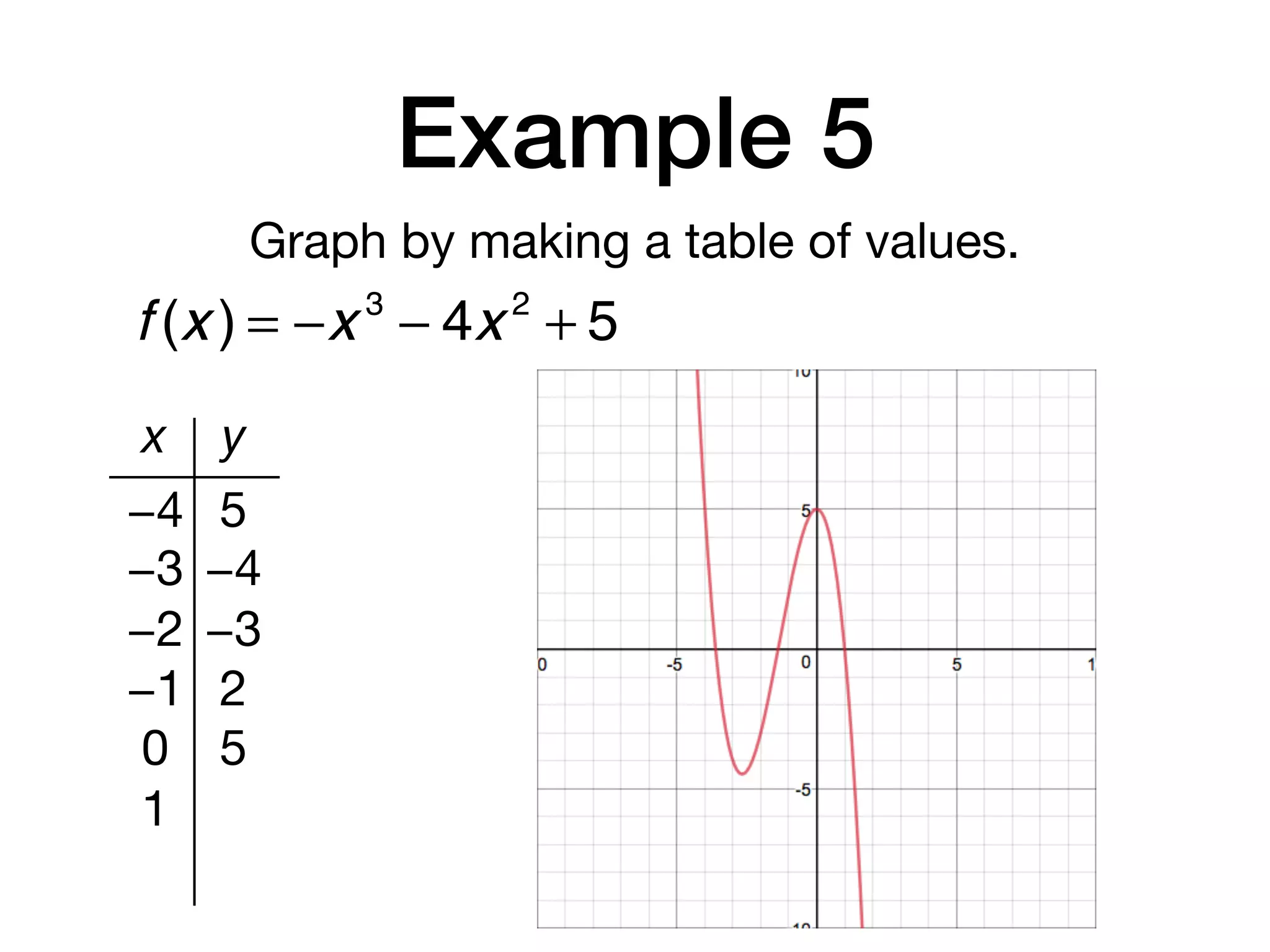
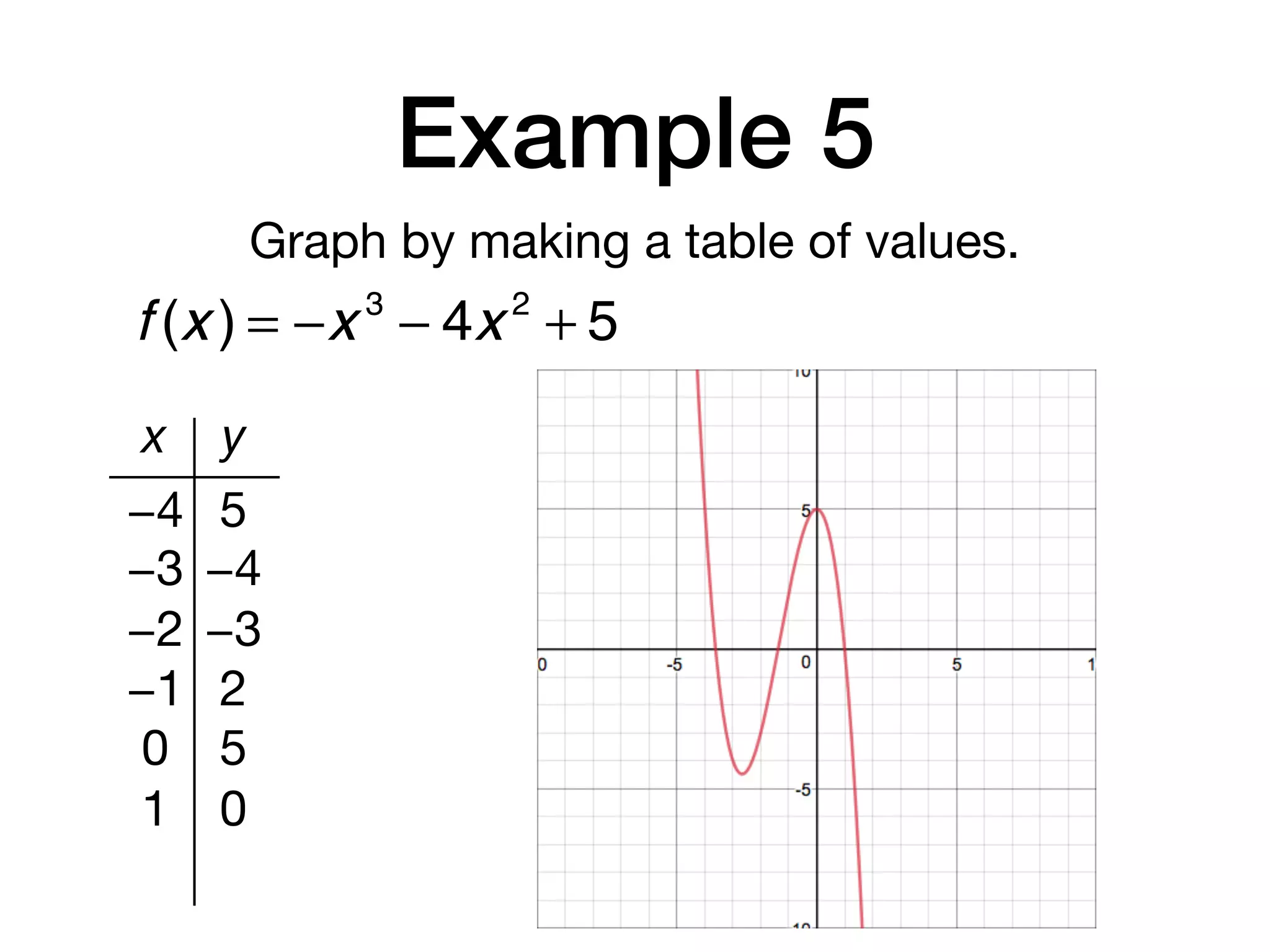
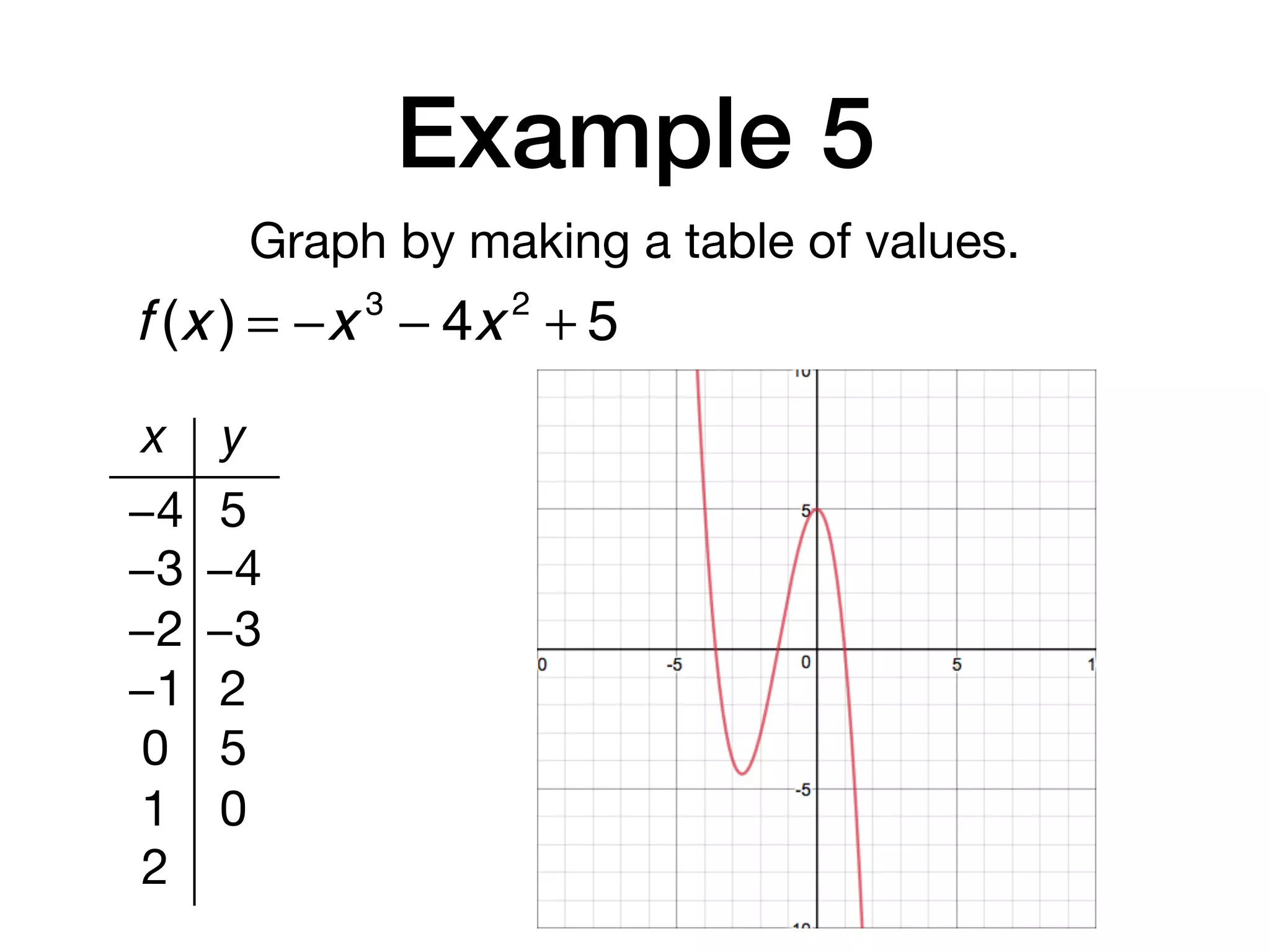
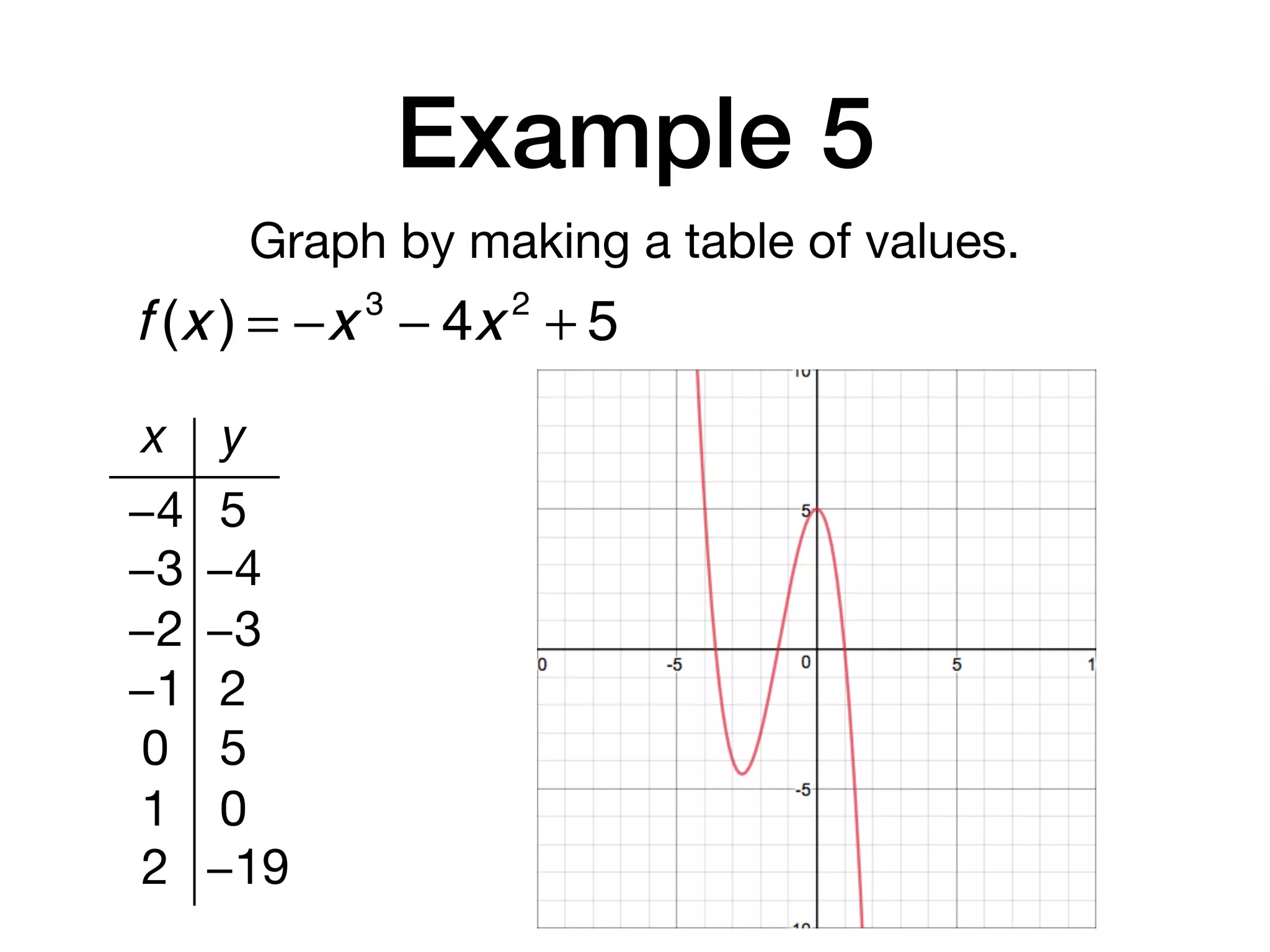
This document discusses polynomial functions. It defines key terms like polynomial in one variable, leading coefficient, and polynomial function. It provides examples of power functions of varying degrees like quadratic, cubic, quartic and quintic functions. The document also includes examples of evaluating polynomial functions, finding degrees and leading coefficients, graphing polynomial functions from tables of values, and describing properties of graphs.

1. Section 4-4
Graphing Polynomial Functions

2. Essential Questions
• How do you evaluate polynomial functions?
• How do you identify general shapes of graphs of
polynomial functions?

3. Vocabulary
1. Polynomial in One Variable:
2. Leading Coefficient:
3. Polynomial Function:

4. Vocabulary
1. Polynomial in One Variable: An expression
with only one variable with varying
exponents and real number coefficients
2. Leading Coefficient:
3. Polynomial Function:

5. Vocabulary
1. Polynomial in One Variable: An expression
with only one variable with varying
exponents and real number coefficients
2. Leading Coefficient: The coefficient of the first
term of a polynomial written in standard
form
3. Polynomial Function:

6. Vocabulary
1. Polynomial in One Variable: An expression
with only one variable with varying
exponents and real number coefficients
2. Leading Coefficient: The coefficient of the first
term of a polynomial written in standard
form
3. Polynomial Function: A continuous function
that can described by a polynomial in one
variable

7. Vocabulary
4. Power Function:
5. Quartic Function:
6. Quintic Function:

8. Vocabulary
4. Power Function: The simplest versions of
polynomial functions of the form
5. Quartic Function:
6. Quintic Function:

9. Vocabulary
4. Power Function: The simplest versions of
polynomial functions of the form
5. Quartic Function:
6. Quintic Function:
f (x ) = axb
, where a and b are nonzero real
numbers

10. Vocabulary
4. Power Function: The simplest versions of
polynomial functions of the form
5. Quartic Function: A power function with a
degree of 4
6. Quintic Function:
f (x ) = axb
, where a and b are nonzero real
numbers

11. Vocabulary
4. Power Function: The simplest versions of
polynomial functions of the form
5. Quartic Function: A power function with a
degree of 4
6. Quintic Function: A power function with a
degree of 5
f (x ) = axb
, where a and b are nonzero real
numbers

12. Power Functions
Constant Function

13. Power Functions
Constant Function
Degree: 0

14. Power Functions
Constant Function
Degree: 0

15. Power Functions
Linear Function

16. Power Functions
Linear Function
Degree: 1

17. Power Functions
Linear Function
Degree: 1

18. Power Functions
Quadratic Function

19. Power Functions
Quadratic Function
Degree: 2

20. Power Functions
Quadratic Function
Degree: 2

21. Power Functions
Cubic Function

22. Power Functions
Cubic Function
Degree: 3

23. Power Functions
Cubic Function
Degree: 3

24. Power Functions
Quartic Function

25. Power Functions
Quartic Function
Degree: 4

26. Power Functions
Quartic Function
Degree: 4

27. Power Functions
Quintic Function

28. Power Functions
Quintic Function
Degree: 5

29. Power Functions
Quintic Function
Degree: 5

30. Example 1
State the degree and leading coefficient of each
polynomial in one variable. If it is not a
polynomial in one variable, explain why.
a. 7z3
− 4z2
+ z

31. Example 1
State the degree and leading coefficient of each
polynomial in one variable. If it is not a
polynomial in one variable, explain why.
a. 7z3
− 4z2
+ z
Degree: 3

32. Example 1
State the degree and leading coefficient of each
polynomial in one variable. If it is not a
polynomial in one variable, explain why.
a. 7z3
− 4z2
+ z
Degree: 3
Leading Coefficient: 7

33. Example 1
State the degree and leading coefficient of each
polynomial in one variable. If it is not a
polynomial in one variable, explain why.
b. 6a3
− 4a2
+ ab2

34. Example 1
State the degree and leading coefficient of each
polynomial in one variable. If it is not a
polynomial in one variable, explain why.
b. 6a3
− 4a2
+ ab2
Not a polynomial in one variable; Has a and b

35. Example 1
State the degree and leading coefficient of each
polynomial in one variable. If it is not a
polynomial in one variable, explain why.
c. 3x5
+ 2x 2
− 4 − 8x 6

36. Example 1
State the degree and leading coefficient of each
polynomial in one variable. If it is not a
polynomial in one variable, explain why.
c. 3x5
+ 2x 2
− 4 − 8x 6
Degree: 6

37. Example 1
State the degree and leading coefficient of each
polynomial in one variable. If it is not a
polynomial in one variable, explain why.
c. 3x5
+ 2x 2
− 4 − 8x 6
Degree: 6
Leading Coefficient: −8

38. Example 2
The volume of the air in the lungs during a 5
second respiratory cycle can be modeled by the
function below, where v is the volume in liters
and t is the time in seconds. Find the volume of
air in the lungs 1.5 seconds into the respiratory
cycle.
v (t) = −0.037t 3
+ 0.152t2
+ 0.173t

39. Example 2
The volume of the air in the lungs during a 5
second respiratory cycle can be modeled by the
function below, where v is the volume in liters
and t is the time in seconds. Find the volume of
air in the lungs 1.5 seconds into the respiratory
cycle.
v (t) = −0.037t 3
+ 0.152t2
+ 0.173t
v (1.5) = −0.037(1.5)3
+ 0.152(1.5)2
+ 0.173(1.5)

40. Example 2
The volume of the air in the lungs during a 5
second respiratory cycle can be modeled by the
function below, where v is the volume in liters
and t is the time in seconds. Find the volume of
air in the lungs 1.5 seconds into the respiratory
cycle.
v (t) = −0.037t 3
+ 0.152t2
+ 0.173t
v (1.5) = −0.037(1.5)3
+ 0.152(1.5)2
+ 0.173(1.5)
v (1.5) = .476625

41. Example 2
The volume of the air in the lungs during a 5
second respiratory cycle can be modeled by the
function below, where v is the volume in liters
and t is the time in seconds. Find the volume of
air in the lungs 1.5 seconds into the respiratory
cycle.
v (t) = −0.037t 3
+ 0.152t2
+ 0.173t
v (1.5) = −0.037(1.5)3
+ 0.152(1.5)2
+ 0.173(1.5)
v (1.5) = .476625 liters

42. Example 3
Find b(m) = 2m2
+ m −1b(2x −1)− 3b(x ) if

43. Example 3
Find b(m) = 2m2
+ m −1b(2x −1)− 3b(x ) if
b(2x −1) = 2(2x −1)2
+ (2x −1)−1

44. Example 3
Find b(m) = 2m2
+ m −1b(2x −1)− 3b(x ) if
b(2x −1) = 2(2x −1)2
+ (2x −1)−1
b(2x −1) = 2(4x 2
− 4x +1)+ 2x −1−1

45. Example 3
Find b(m) = 2m2
+ m −1b(2x −1)− 3b(x ) if
b(2x −1) = 2(2x −1)2
+ (2x −1)−1
b(2x −1) = 2(4x 2
− 4x +1)+ 2x −1−1
b(2x −1) = 8x 2
− 8x + 2 + 2x − 2

46. Example 3
Find b(m) = 2m2
+ m −1b(2x −1)− 3b(x ) if
b(2x −1) = 2(2x −1)2
+ (2x −1)−1
b(2x −1) = 2(4x 2
− 4x +1)+ 2x −1−1
b(2x −1) = 8x 2
− 8x + 2 + 2x − 2
b(2x −1) = 8x 2
− 6x

47. Example 3
Find b(m) = 2m2
+ m −1b(2x −1)− 3b(x ) if
b(2x −1) = 2(2x −1)2
+ (2x −1)−1
b(2x −1) = 2(4x 2
− 4x +1)+ 2x −1−1
b(2x −1) = 8x 2
− 8x + 2 + 2x − 2
b(2x −1) = 8x 2
− 6x
3b(x ) = 3(2x 2
+ x −1)

48. Example 3
Find b(m) = 2m2
+ m −1b(2x −1)− 3b(x ) if
b(2x −1) = 2(2x −1)2
+ (2x −1)−1
b(2x −1) = 2(4x 2
− 4x +1)+ 2x −1−1
b(2x −1) = 8x 2
− 8x + 2 + 2x − 2
b(2x −1) = 8x 2
− 6x
3b(x ) = 3(2x 2
+ x −1)
3b(x ) = 6x 2
+ 3x − 3

49. Example 3
Find b(m) = 2m2
+ m −1b(2x −1)− 3b(x ) if
b(2x −1) = 8x 2
− 6x 3b(x ) = 6x 2
+ 3x − 3

50. Example 3
Find b(m) = 2m2
+ m −1b(2x −1)− 3b(x ) if
b(2x −1) = 8x 2
− 6x 3b(x ) = 6x 2
+ 3x − 3
b(2x −1)− 3b(x ) = 8x 2
− 6x − (6x 2
+ 3x − 3)

51. Example 3
Find b(m) = 2m2
+ m −1b(2x −1)− 3b(x ) if
b(2x −1) = 8x 2
− 6x 3b(x ) = 6x 2
+ 3x − 3
b(2x −1)− 3b(x ) = 8x 2
− 6x − (6x 2
+ 3x − 3)
b(2x −1)− 3b(x ) = 8x 2
− 6x − 6x 2
− 3x + 3

52. Example 3
Find b(m) = 2m2
+ m −1b(2x −1)− 3b(x ) if
b(2x −1) = 8x 2
− 6x 3b(x ) = 6x 2
+ 3x − 3
b(2x −1)− 3b(x ) = 8x 2
− 6x − (6x 2
+ 3x − 3)
b(2x −1)− 3b(x ) = 8x 2
− 6x − 6x 2
− 3x + 3
b(2x −1)− 3b(x ) = 2x 2
− 9x + 3

53. Example 4
For each graph, describe the end behavior,
determine whether it represents an odd degree
or an even degree polynomial function, and
state the number of real zeros.
a.

54. Example 4
For each graph, describe the end behavior,
determine whether it represents an odd degree
or an even degree polynomial function, and
state the number of real zeros.
a.
As x → −∞, f(x) → −∞

55. Example 4
For each graph, describe the end behavior,
determine whether it represents an odd degree
or an even degree polynomial function, and
state the number of real zeros.
a.
As x → −∞, f(x) → −∞
As x → +∞, f(x) → −∞

56. Example 4
For each graph, describe the end behavior,
determine whether it represents an odd degree
or an even degree polynomial function, and
state the number of real zeros.
a.
As x → −∞, f(x) → −∞
As x → +∞, f(x) → −∞
This is an even
degree function

57. Example 4
For each graph, describe the end behavior,
determine whether it represents an odd degree
or an even degree polynomial function, and
state the number of real zeros.
a.
As x → −∞, f(x) → −∞
As x → +∞, f(x) → −∞
This is an even
degree function No real zeros

58. Example 4
For each graph, describe the end behavior,
determine whether it represents an odd degree
or an even degree polynomial function, and
state the number of real zeros.
b.

59. Example 4
For each graph, describe the end behavior,
determine whether it represents an odd degree
or an even degree polynomial function, and
state the number of real zeros.
b.
As x → −∞, f(x) → −∞

60. Example 4
For each graph, describe the end behavior,
determine whether it represents an odd degree
or an even degree polynomial function, and
state the number of real zeros.
b.
As x → −∞, f(x) → −∞
As x → +∞, f(x) → +∞

61. Example 4
For each graph, describe the end behavior,
determine whether it represents an odd degree
or an even degree polynomial function, and
state the number of real zeros.
b.
As x → −∞, f(x) → −∞
As x → +∞, f(x) → +∞
This is an odd
degree function

62. Example 4
For each graph, describe the end behavior,
determine whether it represents an odd degree
or an even degree polynomial function, and
state the number of real zeros.
b.
As x → −∞, f(x) → −∞
As x → +∞, f(x) → +∞
This is an odd
degree function One real zero

63. Example 5
Graph by making a table of values.
f (x ) = −x 3
− 4x 2
+ 5

64. Example 5
Graph by making a table of values.
x y
f (x ) = −x 3
− 4x 2
+ 5

65. Example 5
Graph by making a table of values.
x y
−4
f (x ) = −x 3
− 4x 2
+ 5

66. Example 5
Graph by making a table of values.
x y
−4 5
f (x ) = −x 3
− 4x 2
+ 5

67. Example 5
Graph by making a table of values.
x y
−4 5
−3
f (x ) = −x 3
− 4x 2
+ 5

68. Example 5
Graph by making a table of values.
x y
−4 5
−3 −4
f (x ) = −x 3
− 4x 2
+ 5

69. Example 5
Graph by making a table of values.
x y
−4 5
−3 −4
−2
f (x ) = −x 3
− 4x 2
+ 5

70. Example 5
Graph by making a table of values.
x y
−4 5
−3 −4
−2 −3
f (x ) = −x 3
− 4x 2
+ 5

71. Example 5
Graph by making a table of values.
x y
−4 5
−3 −4
−2 −3
−1
f (x ) = −x 3
− 4x 2
+ 5

72. Example 5
Graph by making a table of values.
x y
−4 5
−3 −4
−2 −3
−1 2
f (x ) = −x 3
− 4x 2
+ 5

73. Example 5
Graph by making a table of values.
x y
−4 5
−3 −4
−2 −3
−1 2
0
f (x ) = −x 3
− 4x 2
+ 5

74. Example 5
Graph by making a table of values.
x y
−4 5
−3 −4
−2 −3
−1 2
0 5
f (x ) = −x 3
− 4x 2
+ 5

75. Example 5
Graph by making a table of values.
x y
−4 5
−3 −4
−2 −3
−1 2
0 5
1
f (x ) = −x 3
− 4x 2
+ 5

76. Example 5
Graph by making a table of values.
x y
−4 5
−3 −4
−2 −3
−1 2
0 5
1 0
f (x ) = −x 3
− 4x 2
+ 5

77. Example 5
Graph by making a table of values.
x y
−4 5
−3 −4
−2 −3
−1 2
0 5
1 0
2
f (x ) = −x 3
− 4x 2
+ 5

78. Example 5
Graph by making a table of values.
x y
−4 5
−3 −4
−2 −3
−1 2
0 5
1 0
2 −19
f (x ) = −x 3
− 4x 2
+ 5