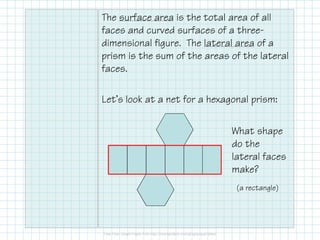
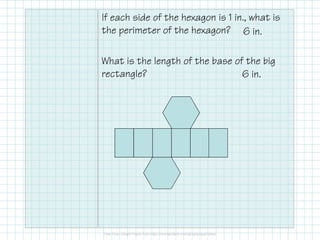
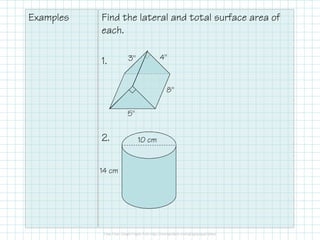
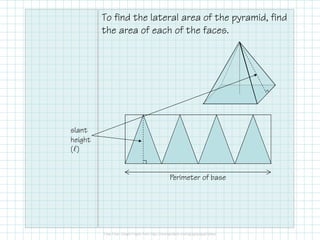
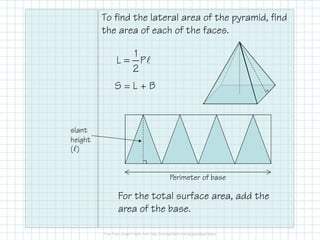
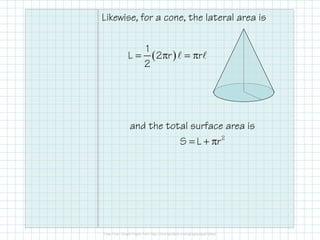
This document discusses how to calculate the surface area of various 3D shapes like prisms, cylinders, pyramids and cones. It provides formulas to find the lateral area and total surface area of each shape. For prisms and cylinders, the lateral area is calculated using the perimeter/circumference and height, while the total area adds the lateral area and both bases. Pyramids and cones use similar formulas involving the perimeter/circumference, slant or lateral height, and the base area. Examples are provided to demonstrate calculating the lateral and total surface areas of different shapes.

1. 5.13.4 Surface Area
The student is able to (I can):
• Calculate the surface area prisms, cylinders, pyramids,
and cones

2. The surface area is the total area of all
faces and curved surfaces of a three-
dimensional figure. The lateral area of a
prism is the sum of the areas of the lateral
faces.
Let’s look at a net for a hexagonal prism:
What shape
do the
lateral faces
make?
(a rectangle)

3. If each side of the hexagon is 1 in., what is
the perimeter of the hexagon?
What is the length of the base of the big
rectangle?
6 in.
6 in.

4. This relationship leads to the formula for
the lateral area of a prism:
L = Ph
where P is the perimeter and h is the height
of the prism.
For the total surface area, add the areas
of the two bases:
S = L + 2B

5. We know that a net of a cylinder looks like:
The length of the lateral surface is the
circumference of the circle, so the formula
changes to:
L = Ch where C = πd or 2πr
and the formula for the total area is now:
S = L + 2πr2

6. Examples Find the lateral and total surface area of
each.
1.
2. 10 cm
14 cm
4"3"
8"
5"

7. Examples Find the lateral and total surface area of
each.
1.
2. 10 cm
14 cm
4"3"
8"
5"
P = 3+4+5 = 12 in.
B = ½(3)(4) = 6 in2
L = (12)(8) = 96 in2
S = 96 + 2(6) = 108 in2
C = 10π cm
B = 52π = 25π cm2
L = (10π)(14) = 140π cm2
S = 140π + 2(25π)
= 190π cm2

8. To find the lateral area of the pyramid, find
the area of each of the faces.
Perimeter of base
slant
height
(ℓ)

9. To find the lateral area of the pyramid, find
the area of each of the faces.
Perimeter of base
slant
height
(ℓ)
1
L P
2
= ℓ
For the total surface area, add the
area of the base.
S = L + B

10. Likewise, for a cone, the lateral area is
( )
1
L 2 r r
2
= π = πℓ ℓ
and the total surface area is
2
S L r= + π

11. Examples Find the lateral and surface area of the
following:
1.
2.
8 in.
20 in.
5 m
5 m

12. Examples Find the lateral and surface area of the
following:
1.
2.
8 in.
20 in.
5 m
5 m
2
8 3
B 6
4
 
=  
 
2
96 3 in=
1
L [(6)(8)](20)
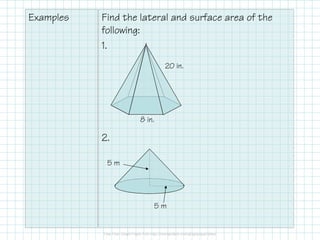
2
=
2
480 in=
2
S 480 96 3 in= +
2
646.3 in≈
5 2 m L (5)(5 2)= π
2
25 2 m= π
2
S 25 2 25 m= π + π
2
189.6 m≈