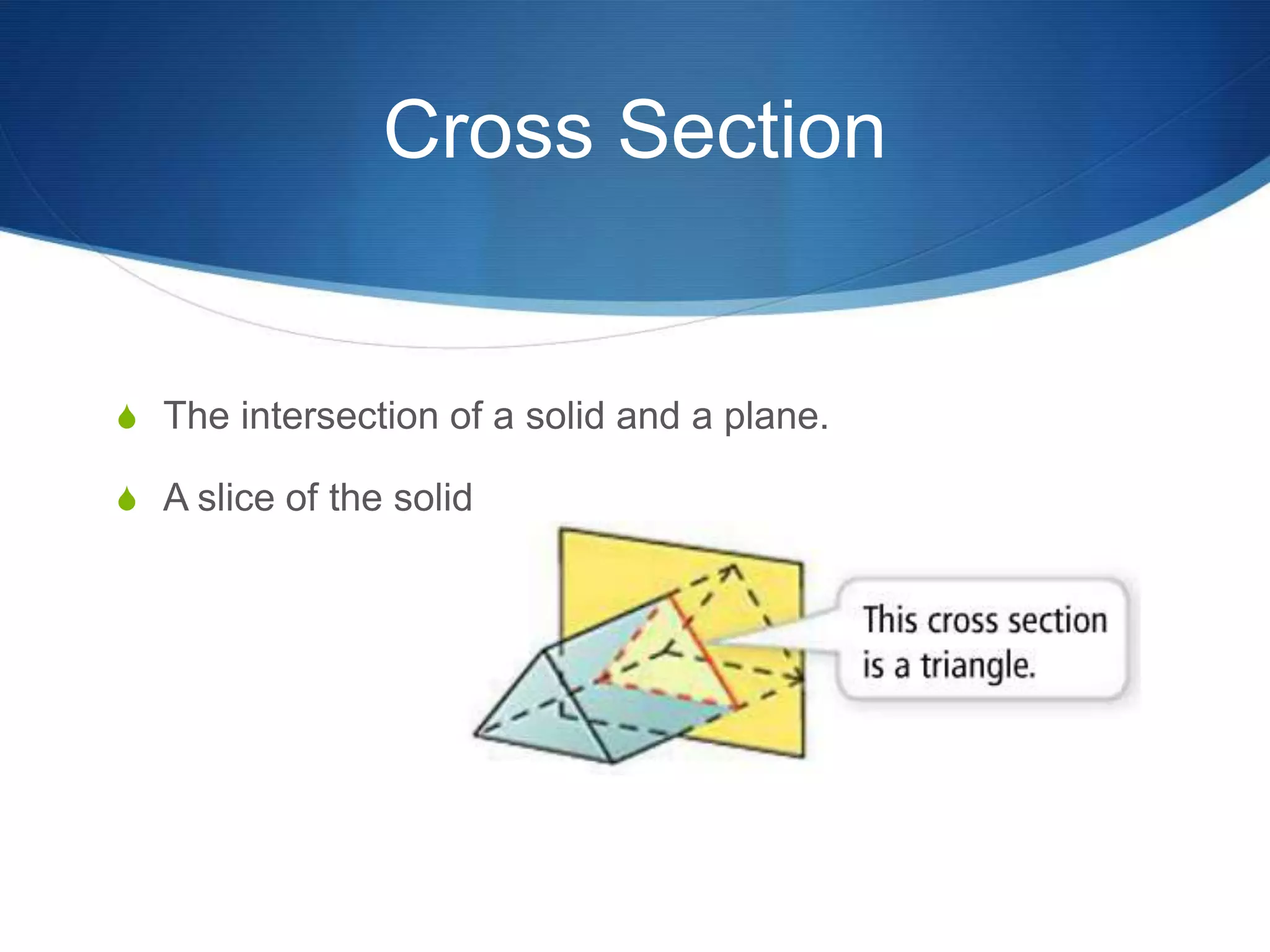
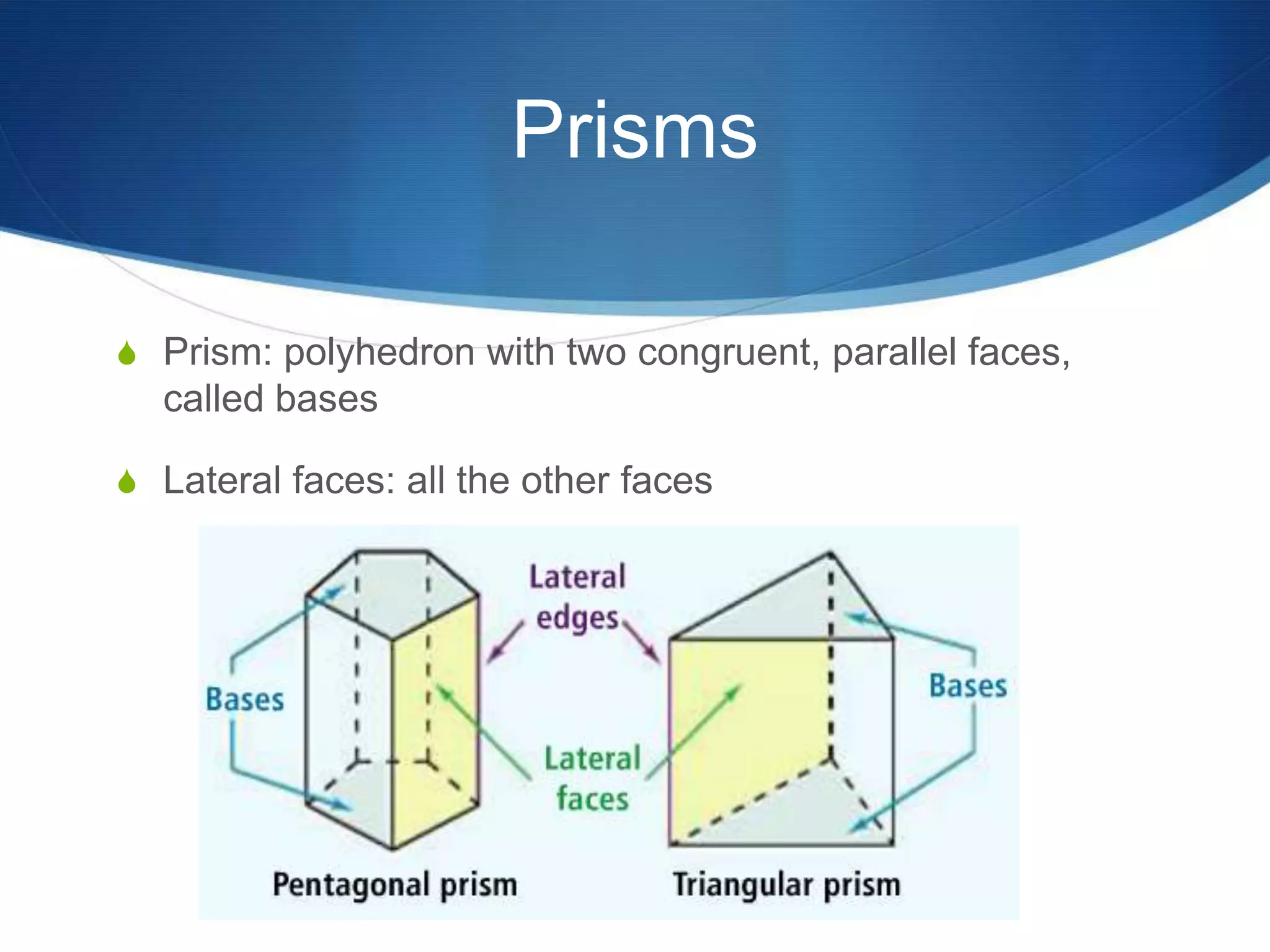
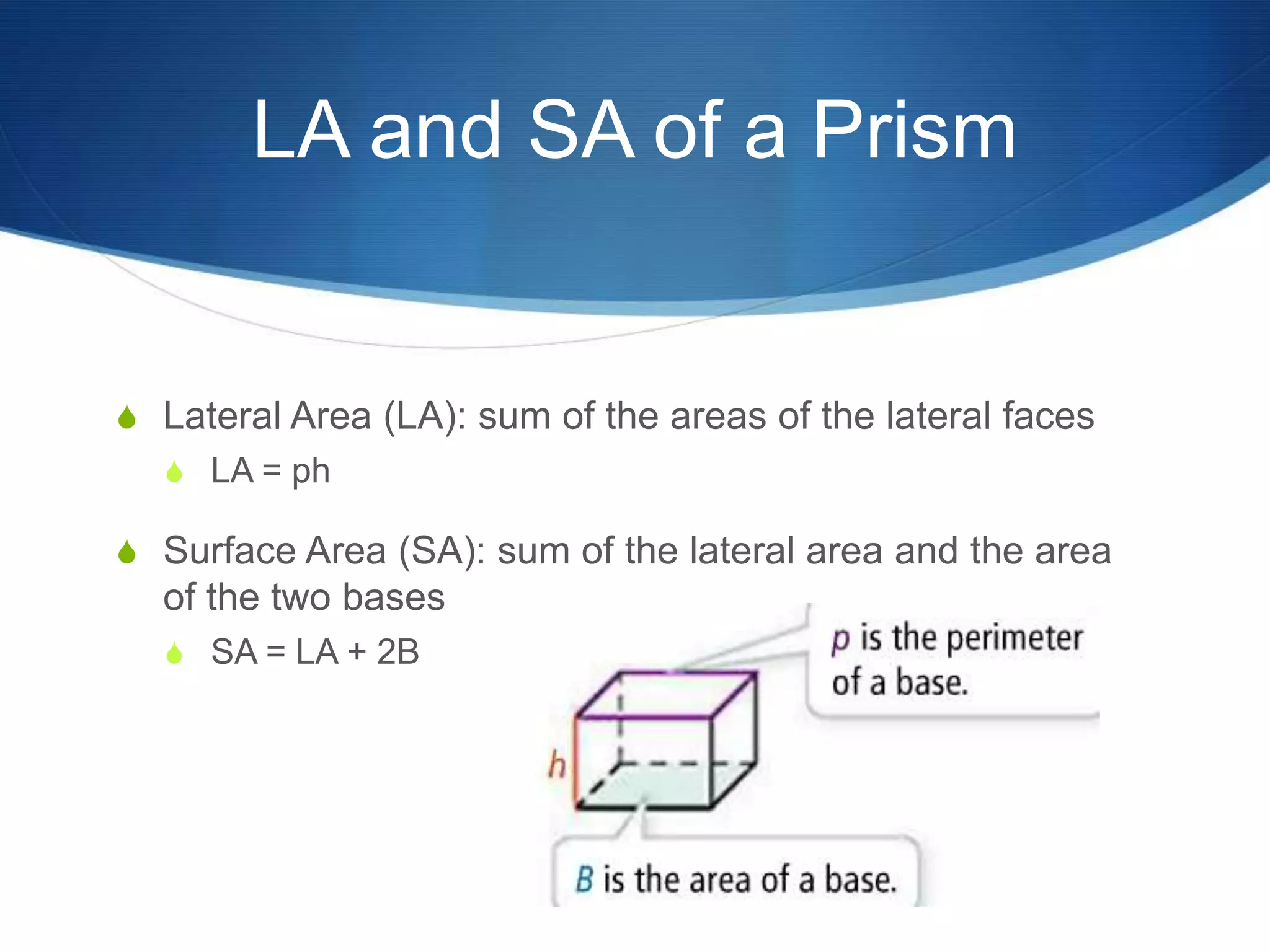
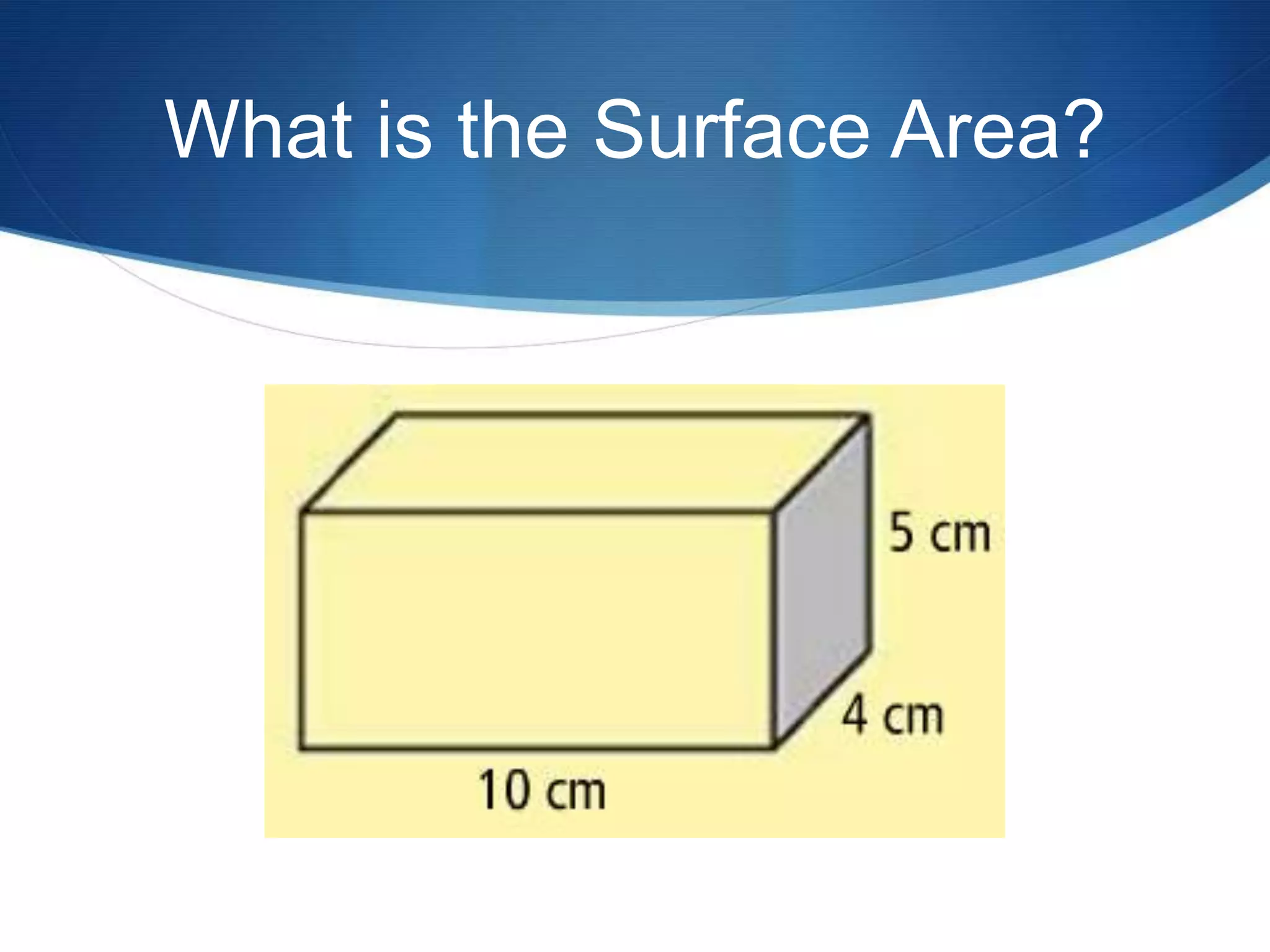
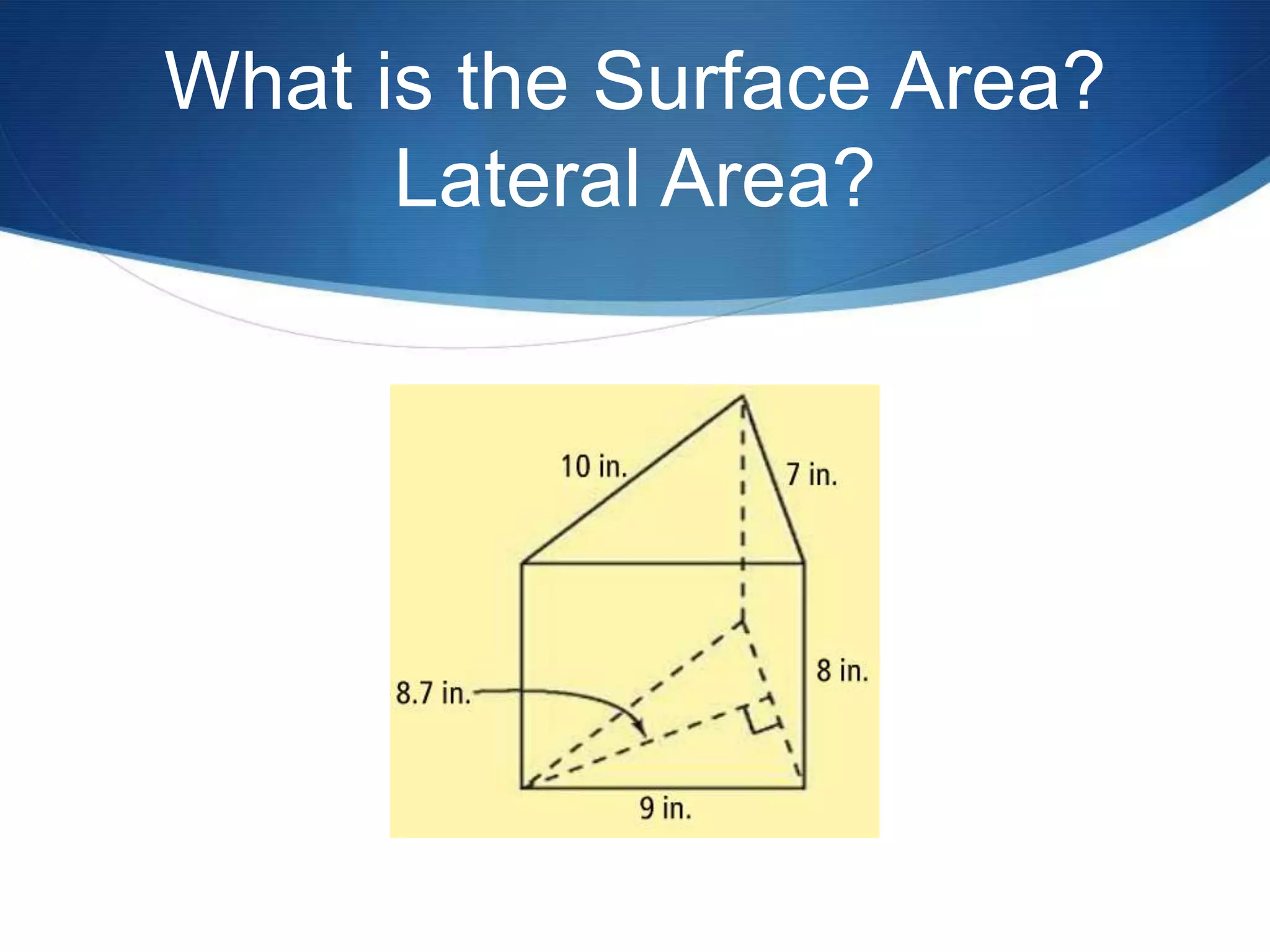
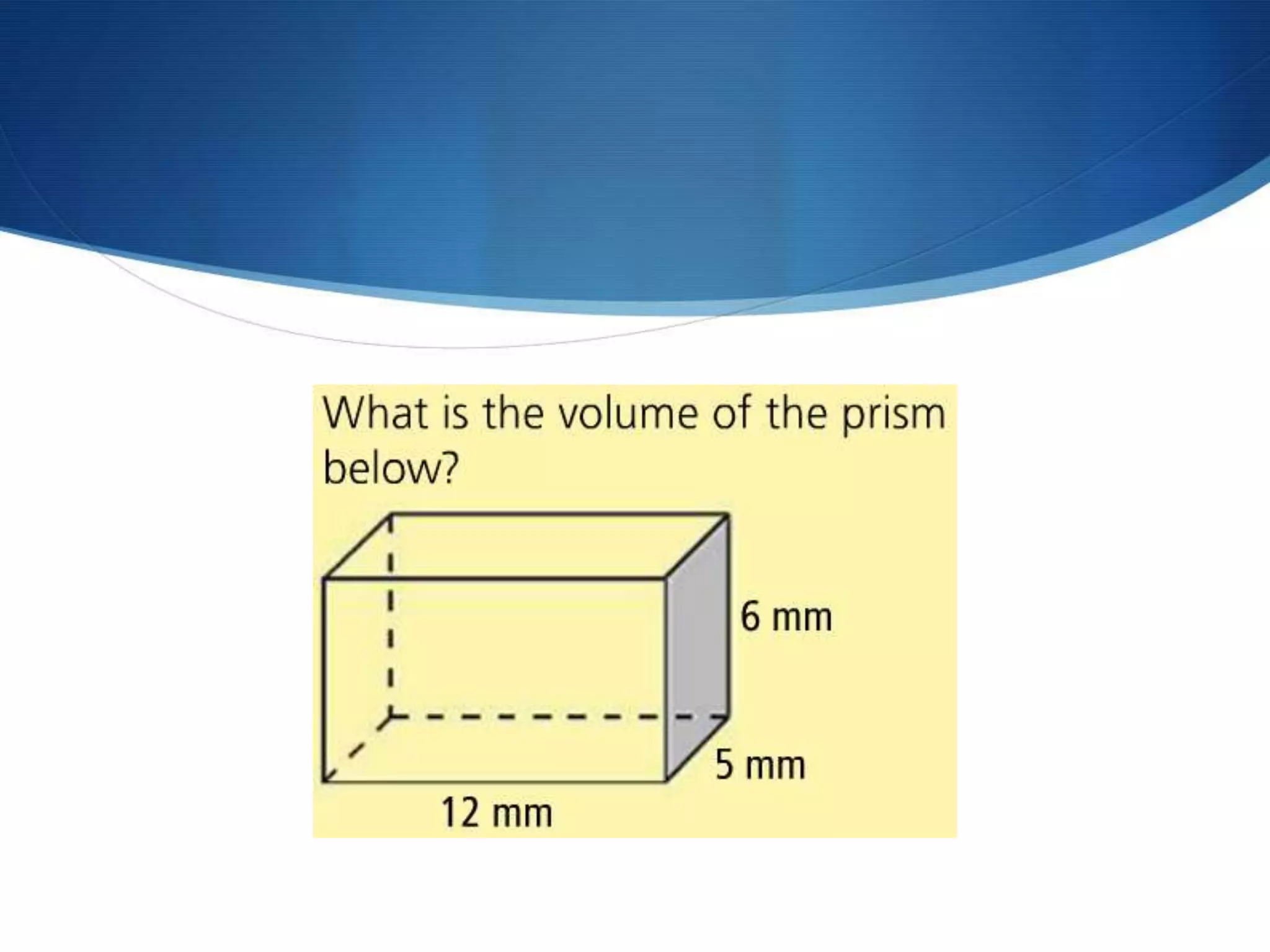
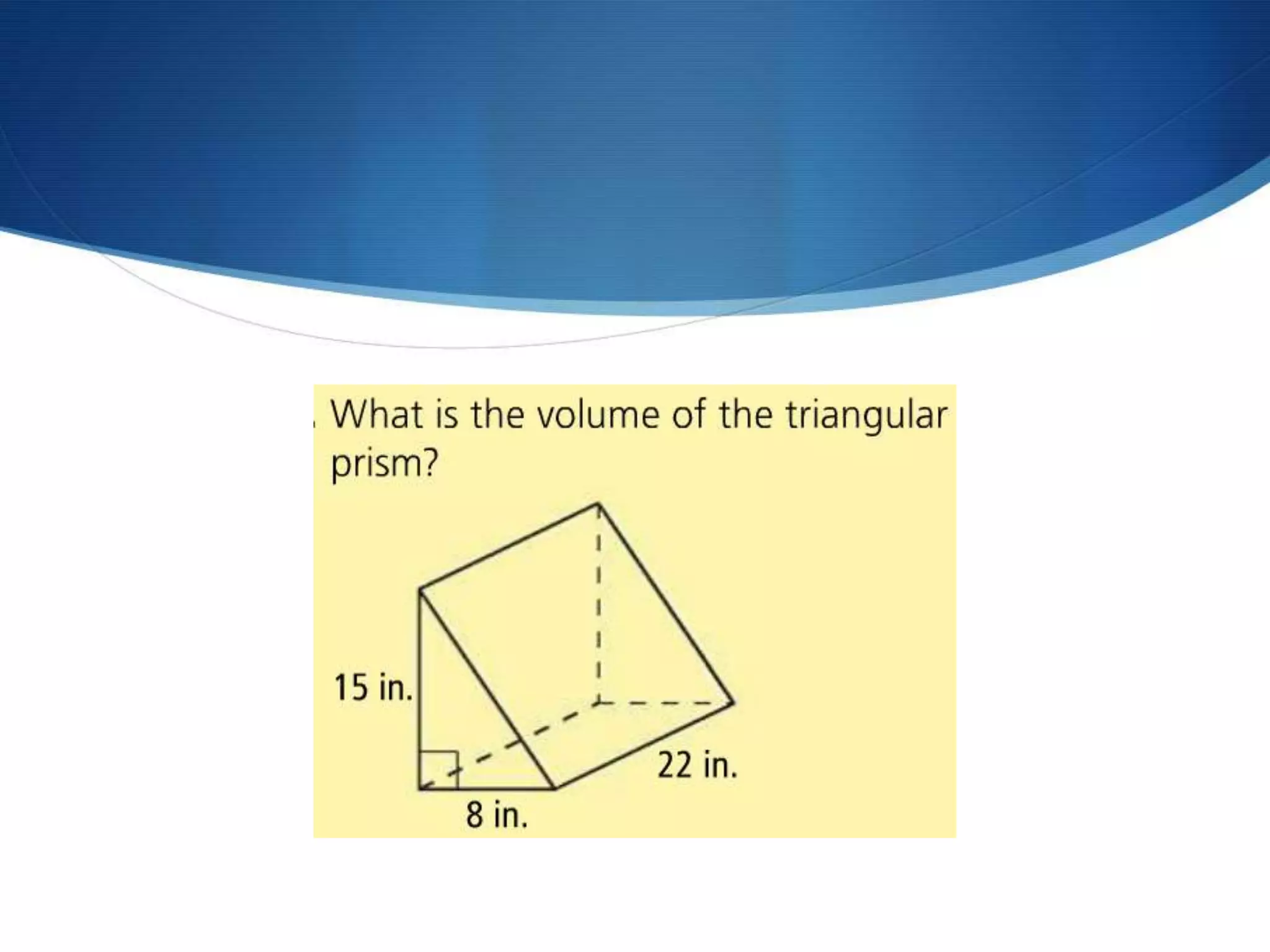
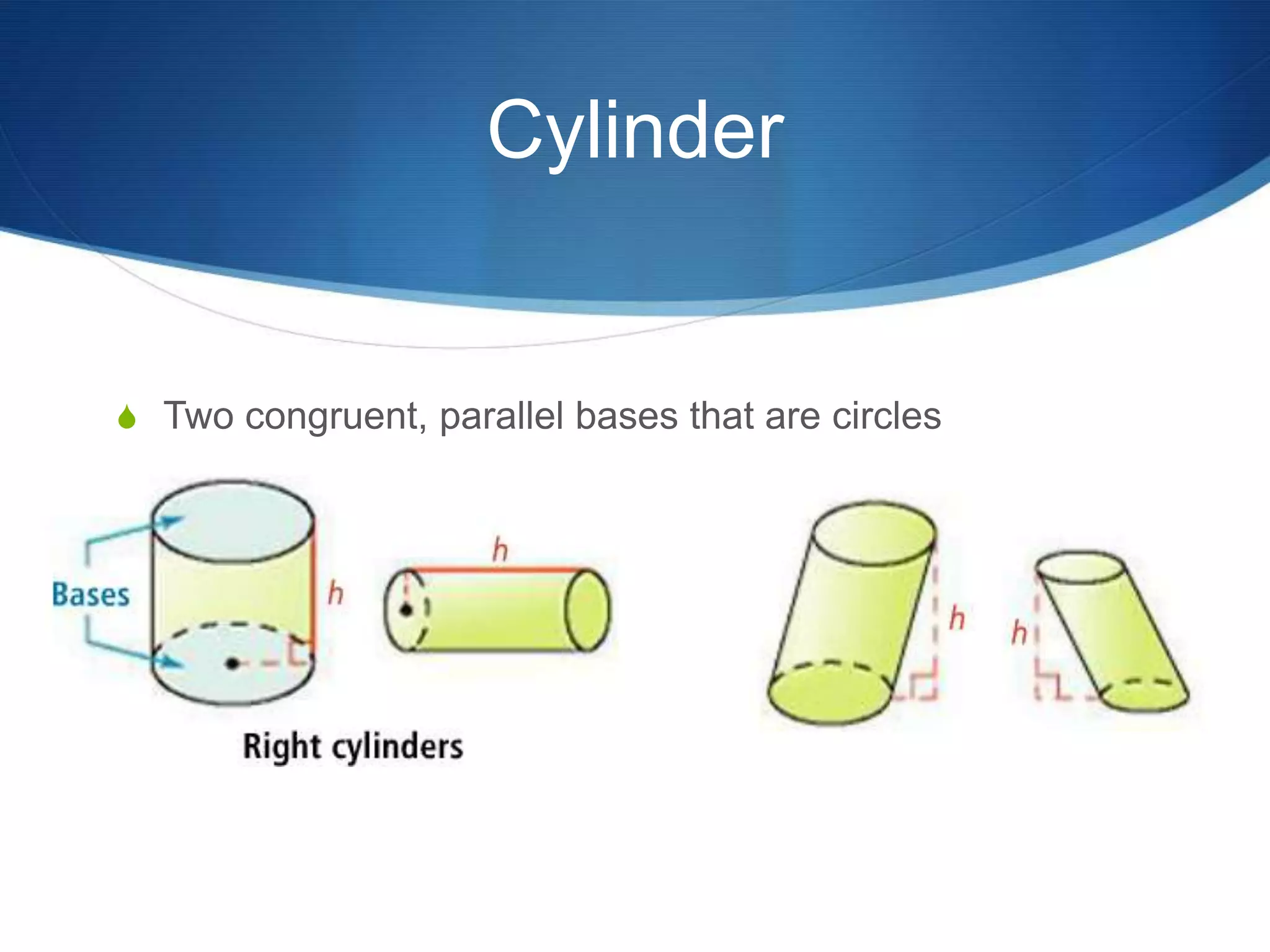
The document provides information about surface area and volume of 3D shapes. It defines polyhedrons, prisms, cylinders, and their key components. It explains how to calculate the surface area of prisms and cylinders by finding the sum of the lateral area and base areas. It also explains how to calculate the volume of prisms and cylinders by multiplying the area of the base by the height. Students are assigned 17 homework problems calculating surface areas and volumes of various prisms and cylinders.

1. Chapter 11 Surface
Area and Volume
11.2 and 11.4
S

2. Essential Understanding
S You can analyze a 3D figure by using the relationship
among its vertices, edges, and faces
S To find the surface area of a 3D figure, find the sum of
the areas of all the surfaces of the figure
S You can find the volume of a prism or cylinder when you
know its height and the area of its base

3. Objectives
S Students will be able to
S recognize polyhedra and their parts
S Visualize cross sections of space figures
S Find the surface area of a prism and a cylinder
S Find the volume of a prism and the volume of a cylinder

4. Polyhedron
S A space figure, or 3D figure whose surfaces are polygons
S Face: each polygon
S Edge: segment formed by the intersection of two faces
S Vertex: point where three or more edges intersect

5. Euler’s Formula
S # Faces + # Vertices = # Edges + 2

6. Cross Section
S The intersection of a solid and a plane.
S A slice of the solid

7. What is the cross section
formed?

8. Prisms
S Prism: polyhedron with two congruent, parallel faces,
called bases
S Lateral faces: all the other faces

9. Prisms…
S Right prism: the lateral faces are rectangles and a lateral
edge is an altitude
S Oblique Prism: some or all of the lateral faces are
nonrectangular.
S (For this chapter, assume that a prism is a right prism
unless otherwise stated)

10. LA and SA of a Prism
S Lateral Area (LA): sum of the areas of the lateral faces
S LA = ph
S Surface Area (SA): sum of the lateral area and the area
of the two bases
S SA = LA + 2B

11. What is the Surface Area?

12. What is the Surface Area?
Lateral Area?

13. Volume of a Prism
S Volume = Base times height
S V = Bh

16. Cylinder
S Two congruent, parallel bases that are circles

17. LA and SA of a Cylinder
S Lateral Surface Area (LA): circumference of the base and
the height of the cylinder
S LA = 2πr * h
OR
S LA = πdh
S Surface Area (SA): Sum of the lateral surface
area the two bases
S SA = LA + 2B
S SA = 2πrh + 2πr2

19. Volume of a Cylinder
S Volume = Base times height
S V = Bh
S V = πr2h

21. Composite Space Figure
S 3D figure that is a combination of two or more simpler
figures
S To find the volume of a composite space figure, add the
volumes of the figures that are combined

23. Homework
S Pg. 704
S #10 – 20 even, 26 (8 problems)
S Pg. 721
S #6 – 20 even, 38 (9 problems)
S 17 total problems