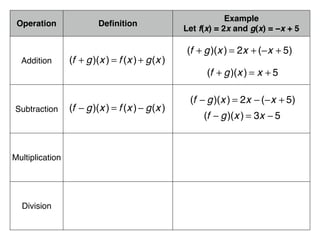
The document discusses operations that can be performed on functions, including addition, subtraction, multiplication, and division. Definitions of each operation are provided, along with examples of applying the operations to specific functions. Addition of functions involves adding the outputs of each function, subtraction involves subtracting the outputs, multiplication involves multiplying the outputs, and division involves dividing the outputs given the denominator function is not equal to 0. Several examples are worked through applying the different operations to functions like f(x)=2x and g(x)=-x+5. The examples also demonstrate evaluating composite functions and restricting domains as needed.

1. Section 5-1
Operations with Functions

2. Essential Questions
• How do you perform arithmetic operations
with functions?
• How do you apply arithmetic operations with
functions?

3. Operation Definition
Example
Let f(x) = 2x and g(x) = −x + 5
Addition
Subtraction
Multiplication
Division

4. Operation Definition
Example
Let f(x) = 2x and g(x) = −x + 5
Addition
Subtraction
Multiplication
Division
(f + g)(x ) = f (x )+ g(x )

5. Operation Definition
Example
Let f(x) = 2x and g(x) = −x + 5
Addition
Subtraction
Multiplication
Division
(f + g)(x ) = f (x )+ g(x )
(f + g)(x ) = 2x + (−x + 5)

6. Operation Definition
Example
Let f(x) = 2x and g(x) = −x + 5
Addition
Subtraction
Multiplication
Division
(f + g)(x ) = f (x )+ g(x )
(f + g)(x ) = 2x + (−x + 5)
(f + g)(x ) = x + 5

7. Operation Definition
Example
Let f(x) = 2x and g(x) = −x + 5
Addition
Subtraction
Multiplication
Division
(f + g)(x ) = f (x )+ g(x )
(f + g)(x ) = 2x + (−x + 5)
(f − g)(x ) = f (x )− g(x )
(f + g)(x ) = x + 5

8. Operation Definition
Example
Let f(x) = 2x and g(x) = −x + 5
Addition
Subtraction
Multiplication
Division
(f + g)(x ) = f (x )+ g(x )
(f + g)(x ) = 2x + (−x + 5)
(f − g)(x ) = f (x )− g(x )
(f − g)(x ) = 2x − (−x + 5)
(f + g)(x ) = x + 5

9. Operation Definition
Example
Let f(x) = 2x and g(x) = −x + 5
Addition
Subtraction
Multiplication
Division
(f + g)(x ) = f (x )+ g(x )
(f + g)(x ) = 2x + (−x + 5)
(f − g)(x ) = 3x − 5
(f − g)(x ) = f (x )− g(x )
(f − g)(x ) = 2x − (−x + 5)
(f + g)(x ) = x + 5

10. Operation Definition
Example
Let f(x) = 2x and g(x) = −x + 5
Addition
Subtraction
Multiplication
Division
(f + g)(x ) = f (x )+ g(x )
(f + g)(x ) = 2x + (−x + 5)
(f − g)(x ) = 3x − 5
(f − g)(x ) = f (x )− g(x )
(f − g)(x ) = 2x − (−x + 5)
(f + g)(x ) = x + 5
(f i g)(x ) = f (x )i g(x )

11. Operation Definition
Example
Let f(x) = 2x and g(x) = −x + 5
Addition
Subtraction
Multiplication
Division
(f + g)(x ) = f (x )+ g(x )
(f + g)(x ) = 2x + (−x + 5)
(f − g)(x ) = 3x − 5
(f − g)(x ) = f (x )− g(x )
(f − g)(x ) = 2x − (−x + 5)
(f + g)(x ) = x + 5
(f i g)(x ) = f (x )i g(x )
(f i g)(x ) = 2x(−x + 5)

12. Operation Definition
Example
Let f(x) = 2x and g(x) = −x + 5
Addition
Subtraction
Multiplication
Division
(f + g)(x ) = f (x )+ g(x )
(f + g)(x ) = 2x + (−x + 5)
(f − g)(x ) = 3x − 5
(f − g)(x ) = f (x )− g(x )
(f − g)(x ) = 2x − (−x + 5)
(f + g)(x ) = x + 5
(f i g)(x ) = f (x )i g(x )
(f i g)(x ) = −2x 2
+10x
(f i g)(x ) = 2x(−x + 5)

13. Operation Definition
Example
Let f(x) = 2x and g(x) = −x + 5
Addition
Subtraction
Multiplication
Division
(f + g)(x ) = f (x )+ g(x )
(f + g)(x ) = 2x + (−x + 5)
(f − g)(x ) = 3x − 5
(f − g)(x ) = f (x )− g(x )
(f − g)(x ) = 2x − (−x + 5)
(f + g)(x ) = x + 5
(f i g)(x ) = f (x )i g(x )
(f i g)(x ) = −2x 2
+10x
(f i g)(x ) = 2x(−x + 5)
f
g
⎛
⎝⎜
⎞
⎠⎟ (x ) =
f (x )
g(x )
,g(x ) ≠ 0

14. Operation Definition
Example
Let f(x) = 2x and g(x) = −x + 5
Addition
Subtraction
Multiplication
Division
(f + g)(x ) = f (x )+ g(x )
(f + g)(x ) = 2x + (−x + 5)
(f − g)(x ) = 3x − 5
(f − g)(x ) = f (x )− g(x )
(f − g)(x ) = 2x − (−x + 5)
(f + g)(x ) = x + 5
(f i g)(x ) = f (x )i g(x )
(f i g)(x ) = −2x 2
+10x
(f i g)(x ) = 2x(−x + 5)
f
g
⎛
⎝⎜
⎞
⎠⎟ (x ) =
f (x )
g(x )
,g(x ) ≠ 0
f
g
⎛
⎝⎜
⎞
⎠⎟ (x ) =
2x
−x + 5
,x ≠ 5

15. Example 1
Given and ,
find each function.
g(x ) = 2x 2
− x −1f (x ) = 3x 2
+ 7x
(f − g)(x )a. (f + g)(x ) b.

16. Example 1
Given and ,
find each function.
g(x ) = 2x 2
− x −1f (x ) = 3x 2
+ 7x
(f − g)(x )a. (f + g)(x ) b.
= f (x )+ g(x )

17. Example 1
Given and ,
find each function.
g(x ) = 2x 2
− x −1f (x ) = 3x 2
+ 7x
(f − g)(x )a. (f + g)(x ) b.
= f (x )+ g(x )
= 3x 2
+ 7x + 2x 2
− x −1

18. Example 1
Given and ,
find each function.
g(x ) = 2x 2
− x −1f (x ) = 3x 2
+ 7x
(f − g)(x )a. (f + g)(x ) b.
= f (x )+ g(x )
= 3x 2
+ 7x + 2x 2
− x −1
= 5x 2
+ 6x −1

19. Example 1
Given and ,
find each function.
g(x ) = 2x 2
− x −1f (x ) = 3x 2
+ 7x
(f − g)(x )a. (f + g)(x ) b.
= f (x )+ g(x )
= 3x 2
+ 7x + 2x 2
− x −1
= 5x 2
+ 6x −1
= f (x )− g(x )

20. Example 1
Given and ,
find each function.
g(x ) = 2x 2
− x −1f (x ) = 3x 2
+ 7x
(f − g)(x )a. (f + g)(x ) b.
= f (x )+ g(x )
= 3x 2
+ 7x + 2x 2
− x −1
= 5x 2
+ 6x −1
= f (x )− g(x )
= 3x 2
+ 7x − (2x 2
− x −1)

21. Example 1
Given and ,
find each function.
g(x ) = 2x 2
− x −1f (x ) = 3x 2
+ 7x
(f − g)(x )a. (f + g)(x ) b.
= f (x )+ g(x )
= 3x 2
+ 7x + 2x 2
− x −1
= 5x 2
+ 6x −1
= f (x )− g(x )
= 3x 2
+ 7x − (2x 2
− x −1)
= 3x 2
+ 7x − 2x 2
+ x +1

22. Example 1
Given and ,
find each function.
g(x ) = 2x 2
− x −1f (x ) = 3x 2
+ 7x
(f − g)(x )a. (f + g)(x ) b.
= f (x )+ g(x )
= 3x 2
+ 7x + 2x 2
− x −1
= 5x 2
+ 6x −1
= f (x )− g(x )
= 3x 2
+ 7x − (2x 2
− x −1)
= 3x 2
+ 7x − 2x 2
+ x +1
= x 2
+ 8x +1

23. Example 2
Given and ,
find each function. Indicate any restrictions
in the domain or range.
g(x ) = x − 4f (x ) = 3x 2
− 2x +1
a. (f i g)(x )

24. Example 2
Given and ,
find each function. Indicate any restrictions
in the domain or range.
g(x ) = x − 4f (x ) = 3x 2
− 2x +1
a. (f i g)(x )
= f (x )i g(x )

25. Example 2
Given and ,
find each function. Indicate any restrictions
in the domain or range.
g(x ) = x − 4f (x ) = 3x 2
− 2x +1
a. (f i g)(x )
= f (x )i g(x )
= (3x 2
− 2x +1)(x − 4)

26. Example 2
Given and ,
find each function. Indicate any restrictions
in the domain or range.
g(x ) = x − 4f (x ) = 3x 2
− 2x +1
a. (f i g)(x )
= f (x )i g(x )
= (3x 2
− 2x +1)(x − 4)
= 3x 3
−12x 2
− 2x 2
+ 8x + x − 4

27. Example 2
Given and ,
find each function. Indicate any restrictions
in the domain or range.
g(x ) = x − 4f (x ) = 3x 2
− 2x +1
a. (f i g)(x )
= f (x )i g(x )
= (3x 2
− 2x +1)(x − 4)
= 3x 3
−12x 2
− 2x 2
+ 8x + x − 4
= 3x 3
−14x 2
+ 9x − 4

28. Example 2
Given and ,
find each function. Indicate any restrictions
in the domain or range.
g(x ) = x − 4f (x ) = 3x 2
− 2x +1
b.
f
g
⎛
⎝⎜
⎞
⎠⎟ (x )

29. Example 2
Given and ,
find each function. Indicate any restrictions
in the domain or range.
g(x ) = x − 4f (x ) = 3x 2
− 2x +1
b.
f
g
⎛
⎝⎜
⎞
⎠⎟ (x )
=
f (x )
g(x )

30. Example 2
Given and ,
find each function. Indicate any restrictions
in the domain or range.
g(x ) = x − 4f (x ) = 3x 2
− 2x +1
b.
f
g
⎛
⎝⎜
⎞
⎠⎟ (x )
=
f (x )
g(x )
=
3x 2
− 2x +1
x − 4

31. Example 2
Given and ,
find each function. Indicate any restrictions
in the domain or range.
g(x ) = x − 4f (x ) = 3x 2
− 2x +1
b.
f
g
⎛
⎝⎜
⎞
⎠⎟ (x )
=
f (x )
g(x )
=
3x 2
− 2x +1
x − 4
; x ≠ 4

32. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
a. Write a function C(x) that represents the total
cost of the tickets, where x is the number of
students on the trip.

33. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
a. Write a function C(x) that represents the total
cost of the tickets, where x is the number of
students on the trip.
C(x ) = 3(24)+15x

34. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
a. Write a function C(x) that represents the total
cost of the tickets, where x is the number of
students on the trip.
C(x ) = 3(24)+15x
C(x ) = 15x + 72

35. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
b. Everyone who goes on the trip will split the
total cost of the tickets evenly. Write a function
N(x) to represent the number of people who will
contribute.

36. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
b. Everyone who goes on the trip will split the
total cost of the tickets evenly. Write a function
N(x) to represent the number of people who will
contribute.
N(x ) = x + 3

37. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
c. Find and explain what this function
represents.
C
N
⎛
⎝⎜
⎞
⎠⎟ (x )

38. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
c. Find and explain what this function
represents.
C
N
⎛
⎝⎜
⎞
⎠⎟ (x )
C(x ) = 15x + 72

39. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
c. Find and explain what this function
represents.
N(x ) = x + 3
C
N
⎛
⎝⎜
⎞
⎠⎟ (x )
C(x ) = 15x + 72

40. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
c. Find and explain what this function
represents.
N(x ) = x + 3
C
N
⎛
⎝⎜
⎞
⎠⎟ (x )
C(x ) = 15x + 72
C
N
⎛
⎝⎜
⎞
⎠⎟ (x )

41. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
c. Find and explain what this function
represents.
N(x ) = x + 3
C
N
⎛
⎝⎜
⎞
⎠⎟ (x )
C(x ) = 15x + 72
C
N
⎛
⎝⎜
⎞
⎠⎟ (x ) =
15x + 72
x + 3

42. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
c. Find and explain what this function
represents.
N(x ) = x + 3
C
N
⎛
⎝⎜
⎞
⎠⎟ (x )
C(x ) = 15x + 72
C
N
⎛
⎝⎜
⎞
⎠⎟ (x ) =
15x + 72
x + 3
This represents the dollar
amount each person will pay

43. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
d. If 20 students go on the trip, how much will
each person pay?

44. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
d. If 20 students go on the trip, how much will
each person pay?
C
N
⎛
⎝⎜
⎞
⎠⎟ (20)

45. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
d. If 20 students go on the trip, how much will
each person pay?
C
N
⎛
⎝⎜
⎞
⎠⎟ (20) =
15(20)+ 72
(20)+ 3

46. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
d. If 20 students go on the trip, how much will
each person pay?
C
N
⎛
⎝⎜
⎞
⎠⎟ (20) =
15(20)+ 72
(20)+ 3
=
300 + 72
23

47. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
d. If 20 students go on the trip, how much will
each person pay?
C
N
⎛
⎝⎜
⎞
⎠⎟ (20) =
15(20)+ 72
(20)+ 3
=
300 + 72
23
=
372
23

48. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
d. If 20 students go on the trip, how much will
each person pay?
C
N
⎛
⎝⎜
⎞
⎠⎟ (20) =
15(20)+ 72
(20)+ 3
=
300 + 72
23
=
372
23
= $16.18

49. Example 3
Matt Mitarnowski is buying tickets to an
aquarium for a school trip. Adult tickets cost
$24 and student tickets cost $15. There will be
3 adult chaperones on the trip.
d. If 20 students go on the trip, how much will
each person pay?
C
N
⎛
⎝⎜
⎞
⎠⎟ (20) =
15(20)+ 72
(20)+ 3
=
300 + 72
23
=
372
23
= $16.18
Each person will pay $16.18 to cover the cost of the trip.