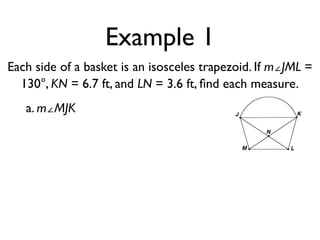
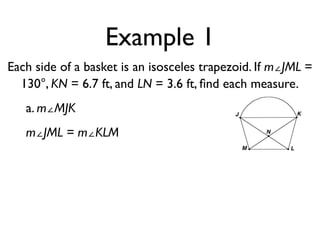
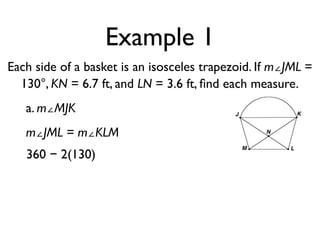
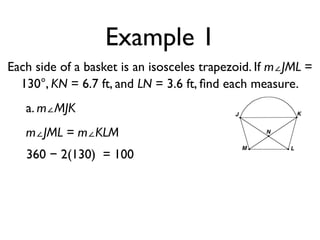
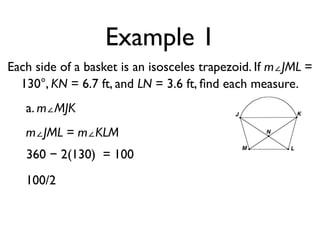
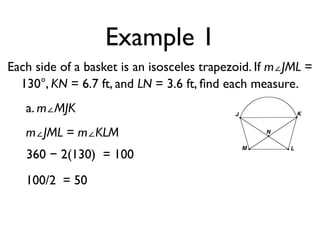
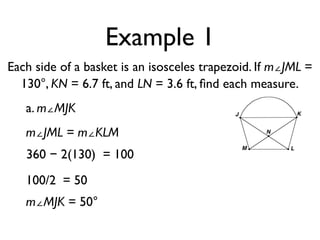
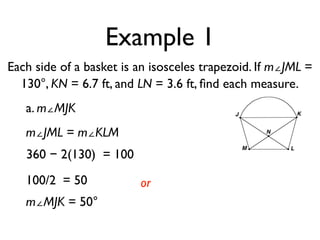
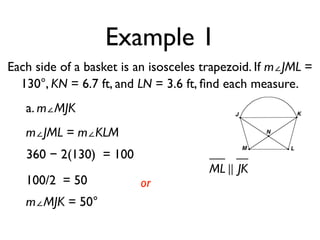
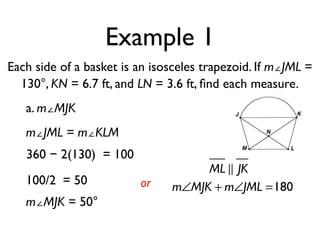
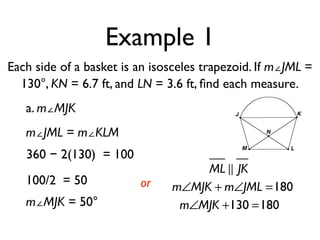
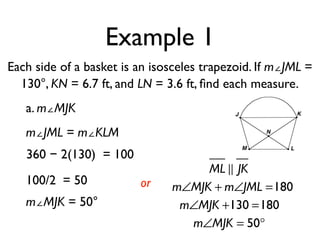
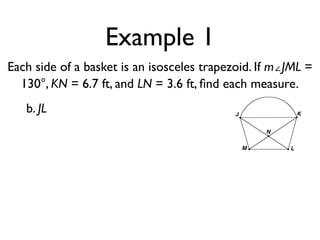
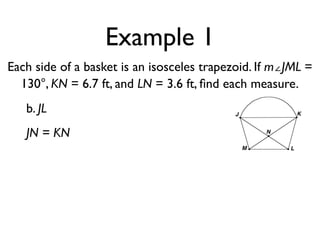
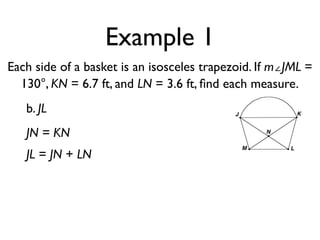
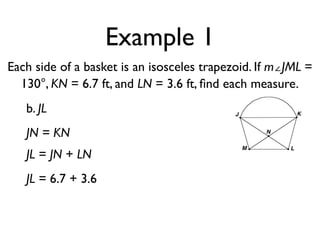
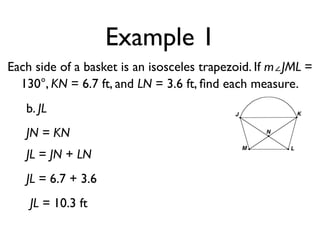
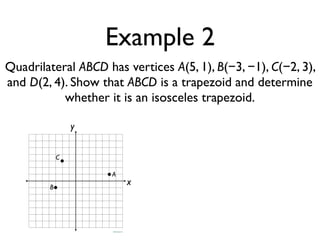
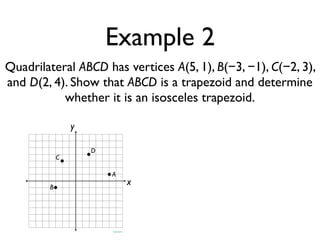
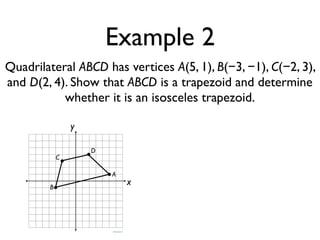
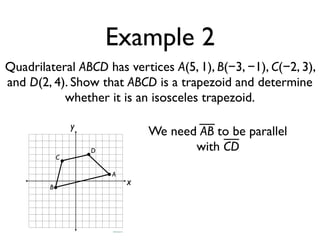
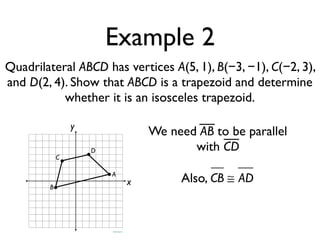
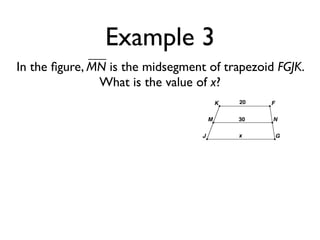
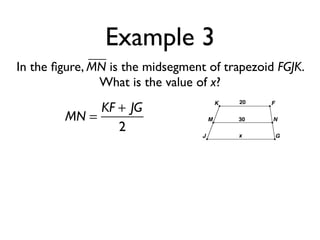
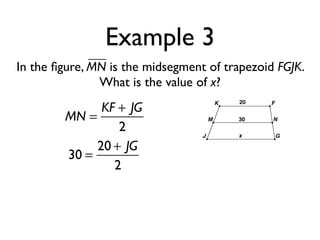
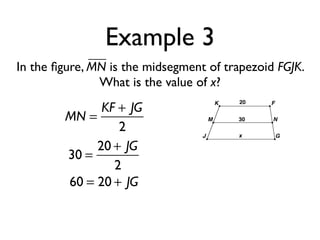
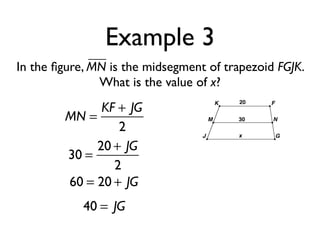
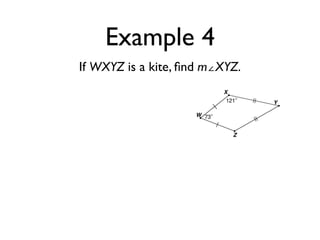
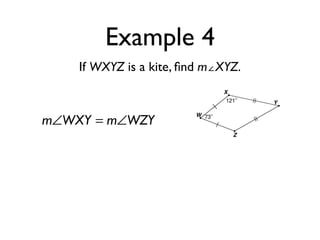
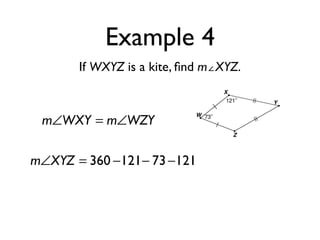
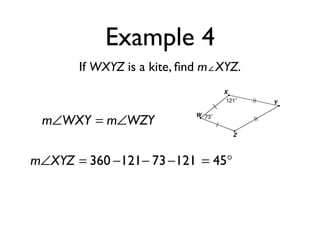
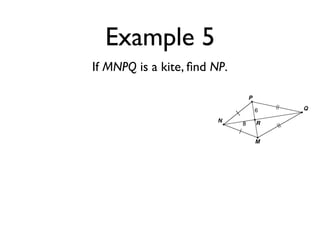
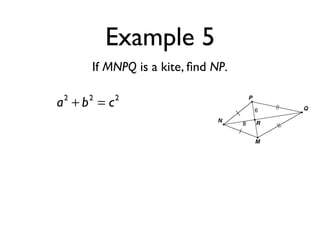
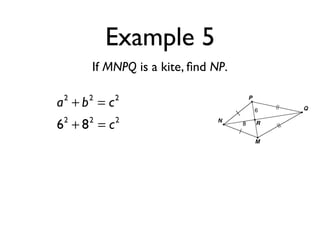
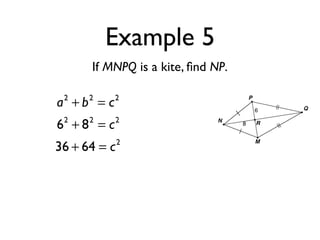
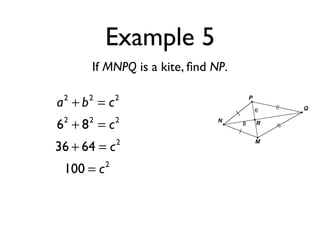
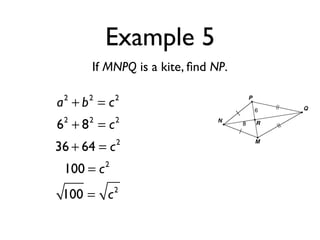
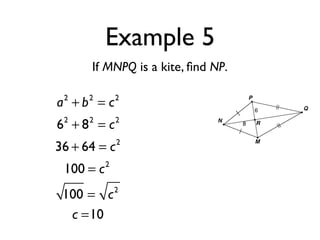
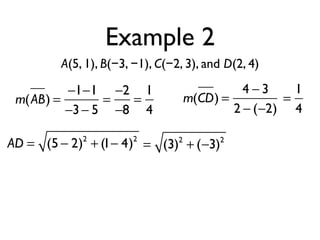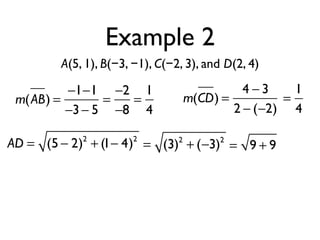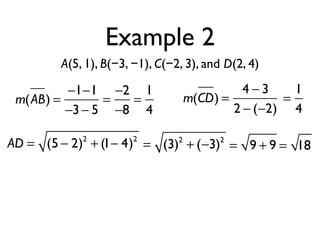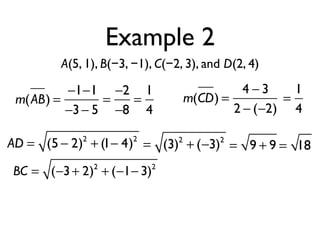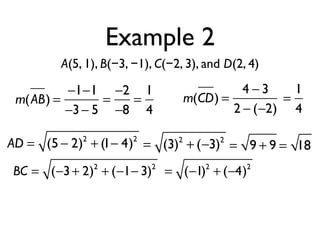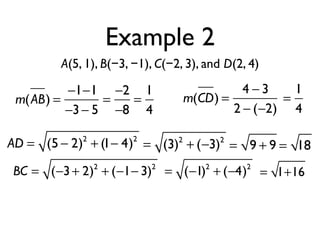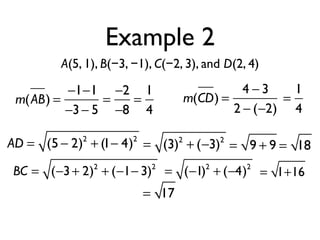The document defines key terms and theorems related to trapezoids and kites. It provides definitions for trapezoid, bases, legs of a trapezoid, base angles, isosceles trapezoid, midsegment of a trapezoid, and kite. It also lists theorems about properties of isosceles trapezoids and kites. Two examples problems are included, one finding measures of an isosceles trapezoid and another showing a quadrilateral is a trapezoid.

1. Section 6-6
Trapezoids and Kites

2. Essential Questions
• How do you apply properties of
trapezoids?
• How do you apply properties of kites?

3. Vocabulary
1.Trapezoid:
2. Bases:
3. Legs of a Trapezoid:
4. Base Angles:
5. Isosceles Trapezoid:

4. Vocabulary
1.Trapezoid: A quadrilateral with only one pair of
parallel sides
2. Bases:
3. Legs of a Trapezoid:
4. Base Angles:
5. Isosceles Trapezoid:

5. Vocabulary
1.Trapezoid: A quadrilateral with only one pair of
parallel sides
2. Bases: The parallel sides of a trapezoid
3. Legs of a Trapezoid:
4. Base Angles:
5. Isosceles Trapezoid:

6. Vocabulary
1.Trapezoid: A quadrilateral with only one pair of
parallel sides
2. Bases: The parallel sides of a trapezoid
3. Legs of a Trapezoid: The sides that are not parallel in a
trapezoid
4. Base Angles:
5. Isosceles Trapezoid:

7. Vocabulary
1.Trapezoid: A quadrilateral with only one pair of
parallel sides
2. Bases: The parallel sides of a trapezoid
3. Legs of a Trapezoid: The sides that are not parallel in a
trapezoid
4. Base Angles: The angles formed between a base and
one of the legs
5. Isosceles Trapezoid:

8. Vocabulary
1.Trapezoid: A quadrilateral with only one pair of
parallel sides
2. Bases: The parallel sides of a trapezoid
3. Legs of a Trapezoid: The sides that are not parallel in a
trapezoid
4. Base Angles: The angles formed between a base and
one of the legs
5. Isosceles Trapezoid: A trapezoid that has congruent
legs

9. Vocabulary
6. Midsegment of a Trapezoid:
7. Kite:

10. Vocabulary
6. Midsegment of a Trapezoid: The segment that
connects the midpoints of the legs of a trapezoid
7. Kite:

11. Vocabulary
6. Midsegment of a Trapezoid: The segment that
connects the midpoints of the legs of a trapezoid
7. Kite: A quadrilateral with exactly two pairs of
consecutive congruent sides; Opposite sides are not
parallel or congruent

12. Theorems
Isosceles Trapezoid
6.21:
6.22:
6.23:

13. Theorems
Isosceles Trapezoid
6.21: If a trapezoid is isosceles, then each pair of base
angles is congruent
6.22:
6.23:

14. Theorems
Isosceles Trapezoid
6.21: If a trapezoid is isosceles, then each pair of base
angles is congruent
6.22: If a trapezoid has one pair of congruent base
angles, then it is isosceles
6.23:

15. Theorems
Isosceles Trapezoid
6.21: If a trapezoid is isosceles, then each pair of base
angles is congruent
6.22: If a trapezoid has one pair of congruent base
angles, then it is isosceles
6.23: A trapezoid is isosceles IFF its diagonals are
congruent

16. Theorems
6.24 - Trapezoid Midsegment Theorem:
Kites
6.25:
6.26:

17. Theorems
6.24 - Trapezoid Midsegment Theorem: The midsegment
of a trapezoid is parallel to each base and its measure
is half of the sum of the lengths of the two bases
Kites
6.25:
6.26:

18. Theorems
6.24 - Trapezoid Midsegment Theorem: The midsegment
of a trapezoid is parallel to each base and its measure
is half of the sum of the lengths of the two bases
Kites
6.25: If a quadrilateral is a kite, then its diagonals are
perpendicular
6.26:

19. Theorems
6.24 - Trapezoid Midsegment Theorem: The midsegment
of a trapezoid is parallel to each base and its measure
is half of the sum of the lengths of the two bases
Kites
6.25: If a quadrilateral is a kite, then its diagonals are
perpendicular
6.26: If a quadrilateral is a kite, then exactly one pair of
opposite angles is congruent

20. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
a. m∠MJK

21. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
a. m∠MJK
m∠JML = m∠KLM

22. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
a. m∠MJK
m∠JML = m∠KLM
360 − 2(130)

23. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
a. m∠MJK
m∠JML = m∠KLM
360 − 2(130) = 100

24. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
a. m∠MJK
m∠JML = m∠KLM
360 − 2(130) = 100
100/2

25. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
a. m∠MJK
m∠JML = m∠KLM
360 − 2(130) = 100
100/2 = 50

26. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
a. m∠MJK
m∠JML = m∠KLM
360 − 2(130) = 100
100/2 = 50
m∠MJK = 50°

27. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
a. m∠MJK
m∠JML = m∠KLM
360 − 2(130) = 100
100/2 = 50
m∠MJK = 50°
or

28. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
a. m∠MJK
m∠JML = m∠KLM
360 − 2(130) = 100
100/2 = 50
m∠MJK = 50°
or
ML ! JK

29. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
a. m∠MJK
m∠JML = m∠KLM
360 − 2(130) = 100
100/2 = 50
m∠MJK = 50°
or
ML ! JK
m∠MJK + m∠JML =180

30. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
a. m∠MJK
m∠JML = m∠KLM
360 − 2(130) = 100
100/2 = 50
m∠MJK = 50°
or
ML ! JK
m∠MJK + m∠JML =180
m∠MJK +130 =180

31. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
a. m∠MJK
m∠JML = m∠KLM
360 − 2(130) = 100
100/2 = 50
m∠MJK = 50°
or
ML ! JK
m∠MJK + m∠JML =180
m∠MJK +130 =180
m∠MJK = 50°

32. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
b. JL

33. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
b. JL
JN = KN

34. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
b. JL
JN = KN
JL = JN + LN

35. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
b. JL
JN = KN
JL = JN + LN
JL = 6.7 + 3.6

36. Example 1
Each side of a basket is an isosceles trapezoid. If m∠JML =
130°, KN = 6.7 ft, and LN = 3.6 ft, find each measure.
b. JL
JN = KN
JL = JN + LN
JL = 6.7 + 3.6
JL = 10.3 ft

37. Example 2
Quadrilateral ABCD has vertices A(5, 1), B(−3, −1), C(−2, 3),
and D(2, 4). Show that ABCD is a trapezoid and determine
whether it is an isosceles trapezoid.

38. Example 2
Quadrilateral ABCD has vertices A(5, 1), B(−3, −1), C(−2, 3),
and D(2, 4). Show that ABCD is a trapezoid and determine
whether it is an isosceles trapezoid.
x
y

39. Example 2
Quadrilateral ABCD has vertices A(5, 1), B(−3, −1), C(−2, 3),
and D(2, 4). Show that ABCD is a trapezoid and determine
whether it is an isosceles trapezoid.
x
y
A

40. Example 2
Quadrilateral ABCD has vertices A(5, 1), B(−3, −1), C(−2, 3),
and D(2, 4). Show that ABCD is a trapezoid and determine
whether it is an isosceles trapezoid.
x
y
A
B

41. Example 2
Quadrilateral ABCD has vertices A(5, 1), B(−3, −1), C(−2, 3),
and D(2, 4). Show that ABCD is a trapezoid and determine
whether it is an isosceles trapezoid.
x
y
A
B
C

42. Example 2
Quadrilateral ABCD has vertices A(5, 1), B(−3, −1), C(−2, 3),
and D(2, 4). Show that ABCD is a trapezoid and determine
whether it is an isosceles trapezoid.
x
y
A
B
C
D

43. Example 2
Quadrilateral ABCD has vertices A(5, 1), B(−3, −1), C(−2, 3),
and D(2, 4). Show that ABCD is a trapezoid and determine
whether it is an isosceles trapezoid.
x
y
A
B
C
D

44. Example 2
Quadrilateral ABCD has vertices A(5, 1), B(−3, −1), C(−2, 3),
and D(2, 4). Show that ABCD is a trapezoid and determine
whether it is an isosceles trapezoid.
x
y
A
B
C
D
We need AB to be parallel
with CD

45. Example 2
Quadrilateral ABCD has vertices A(5, 1), B(−3, −1), C(−2, 3),
and D(2, 4). Show that ABCD is a trapezoid and determine
whether it is an isosceles trapezoid.
x
y
A
B
C
D
We need AB to be parallel
with CD
CB ≅ ADAlso,

46. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)

47. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)
m(AB) =
−1−1
−3− 5

48. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)
m(AB) =
−1−1
−3− 5
=
−2
−8

49. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)
m(AB) =
−1−1
−3− 5
=
−2
−8
=
1
4

50. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)
m(AB) =
−1−1
−3− 5
=
−2
−8
=
1
4
m(CD) =
4 − 3
2 − (−2)

51. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)
m(AB) =
−1−1
−3− 5
=
−2
−8
=
1
4
m(CD) =
4 − 3
2 − (−2)
=
1
4

52. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)
m(AB) =
−1−1
−3− 5
=
−2
−8
=
1
4
m(CD) =
4 − 3
2 − (−2)
=
1
4
AD = (5 − 2)2
+ (1− 4)2

53. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)
m(AB) =
−1−1
−3− 5
=
−2
−8
=
1
4
m(CD) =
4 − 3
2 − (−2)
=
1
4
AD = (5 − 2)2
+ (1− 4)2
= (3)2
+ (−3)2

54. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)
m(AB) =
−1−1
−3− 5
=
−2
−8
=
1
4
m(CD) =
4 − 3
2 − (−2)
=
1
4
AD = (5 − 2)2
+ (1− 4)2
= (3)2
+ (−3)2
= 9 + 9

55. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)
m(AB) =
−1−1
−3− 5
=
−2
−8
=
1
4
m(CD) =
4 − 3
2 − (−2)
=
1
4
AD = (5 − 2)2
+ (1− 4)2
= (3)2
+ (−3)2
= 9 + 9 = 18

56. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)
m(AB) =
−1−1
−3− 5
=
−2
−8
=
1
4
m(CD) =
4 − 3
2 − (−2)
=
1
4
AD = (5 − 2)2
+ (1− 4)2
= (3)2
+ (−3)2
= 9 + 9 = 18
BC = (−3+ 2)2
+ (−1− 3)2

57. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)
m(AB) =
−1−1
−3− 5
=
−2
−8
=
1
4
m(CD) =
4 − 3
2 − (−2)
=
1
4
AD = (5 − 2)2
+ (1− 4)2
= (3)2
+ (−3)2
= 9 + 9 = 18
BC = (−3+ 2)2
+ (−1− 3)2
= (−1)2
+ (−4)2

58. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)
m(AB) =
−1−1
−3− 5
=
−2
−8
=
1
4
m(CD) =
4 − 3
2 − (−2)
=
1
4
AD = (5 − 2)2
+ (1− 4)2
= (3)2
+ (−3)2
= 9 + 9 = 18
BC = (−3+ 2)2
+ (−1− 3)2
= (−1)2
+ (−4)2
= 1+16

59. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)
m(AB) =
−1−1
−3− 5
=
−2
−8
=
1
4
m(CD) =
4 − 3
2 − (−2)
=
1
4
AD = (5 − 2)2
+ (1− 4)2
= (3)2
+ (−3)2
= 9 + 9 = 18
BC = (−3+ 2)2
+ (−1− 3)2
= (−1)2
+ (−4)2
= 1+16
= 17

60. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)
m(AB) =
−1−1
−3− 5
=
−2
−8
=
1
4
m(CD) =
4 − 3
2 − (−2)
=
1
4
AD = (5 − 2)2
+ (1− 4)2
= (3)2
+ (−3)2
= 9 + 9 = 18
BC = (−3+ 2)2
+ (−1− 3)2
= (−1)2
+ (−4)2
= 1+16
= 17
CB ≅ AD

61. Example 2
A(5, 1), B(−3, −1), C(−2, 3), and D(2, 4)
m(AB) =
−1−1
−3− 5
=
−2
−8
=
1
4
m(CD) =
4 − 3
2 − (−2)
=
1
4
AD = (5 − 2)2
+ (1− 4)2
= (3)2
+ (−3)2
= 9 + 9 = 18
BC = (−3+ 2)2
+ (−1− 3)2
= (−1)2
+ (−4)2
= 1+16
= 17
It is a trapezoid, but not isoscelesCB ≅ AD

62. Example 3
In the figure, MN is the midsegment of trapezoid FGJK.
What is the value of x?

63. Example 3
In the figure, MN is the midsegment of trapezoid FGJK.
What is the value of x?
MN =
KF + JG
2

64. Example 3
In the figure, MN is the midsegment of trapezoid FGJK.
What is the value of x?
MN =
KF + JG
2
30 =
20 + JG
2

65. Example 3
In the figure, MN is the midsegment of trapezoid FGJK.
What is the value of x?
MN =
KF + JG
2
30 =
20 + JG
2
60 = 20 + JG

66. Example 3
In the figure, MN is the midsegment of trapezoid FGJK.
What is the value of x?
MN =
KF + JG
2
30 =
20 + JG
2
60 = 20 + JG
40 = JG

67. Example 4
If WXYZ is a kite, find m∠XYZ.

68. Example 4
If WXYZ is a kite, find m∠XYZ.
m∠WXY = m∠WZY

69. Example 4
If WXYZ is a kite, find m∠XYZ.
m∠WXY = m∠WZY
m∠XYZ = 360 −121− 73−121

70. Example 4
If WXYZ is a kite, find m∠XYZ.
m∠WXY = m∠WZY
m∠XYZ = 360 −121− 73−121 = 45°

71. Example 5
If MNPQ is a kite, find NP.

72. Example 5
If MNPQ is a kite, find NP.
a2
+ b2
= c2

73. Example 5
If MNPQ is a kite, find NP.
a2
+ b2
= c2
62
+ 82
= c2

74. Example 5
If MNPQ is a kite, find NP.
a2
+ b2
= c2
62
+ 82
= c2
36 + 64 = c2

75. Example 5
If MNPQ is a kite, find NP.
a2
+ b2
= c2
62
+ 82
= c2
36 + 64 = c2
100 = c2

76. Example 5
If MNPQ is a kite, find NP.
a2
+ b2
= c2
62
+ 82
= c2
36 + 64 = c2
100 = c2
100 = c2

77. Example 5
If MNPQ is a kite, find NP.
a2
+ b2
= c2
62
+ 82
= c2
36 + 64 = c2
100 = c2
100 = c2
c =10