Dokumen ini membahas konsep integral, anti-turunan, dan persamaan diferensial sederhana dalam kalkulus. Diperkenalkan teorema-teorema penting mengenai sifat-sifat integral serta metode pemisahan variabel untuk menyelesaikan persamaan diferensial. Selain itu, dijelaskan juga notasi sigma dan cara menghitung luas daerah di bawah kurva.

1. CALCULUS 2
Amalia Indrawati Gunawan, S.Pd. M.PMat.
in Suryakancana University Cianjur

2. INTEGRAL
• Anti-turunan dan Integral Tak Tentu
• Persamaan Diferensial Sederhana
• Notasi Sigma dan Luas Daerah di
Bawah Kurva
• Integral Tentu
• Teorema Dasar Kalkulus
• Sifat-sifat Integral Tentu Lebih Lanjut
• Substitusi dalam Penghitungan Integral
Tentu

3. Anti-turunan dan Integral Tak Tentu
Fungsi F disebut anti-turunan f pada selang 𝐼 apabila :
𝐹′
𝑥 = 𝑓(𝑥)
Untuk setiap 𝑥 ∈ 𝐼.
Sebagai contoh,
𝐹 𝑥 = 𝑥2 + 1
Merupakan anti turunan dari
𝑓 𝑥 = 2𝑥 pada ℝ
Secara umum, keluarga fungsi 𝐹 𝑥 = 𝑥2
+ 𝐶 merupakan
anti-turunan dari 𝑓 𝑥 = 2𝑥 pada ℝ karena 𝐹′ 𝑥 = 2𝑥 = 𝑓 𝑥
untuk setiap 𝑥 ∈ ℝ.
Keluarga fungsi anti-turunan 𝑓 𝑥 disebut integral tak tentu
dari 𝑓 𝑥 dan dilambangkan dengan 𝑓 𝑥 𝑑𝑥. Jadi, sebagai
contoh,
2𝑥 𝑑𝑥 = 𝑥2
+ 𝐶

4. Anti-turunan dan Integral Tak Tentu
Secara grafik, keluarga fungsi anti-turunan 𝑓 𝑥 adalah
keluarga fungsi yang anggotanya merupakan pergeseran
ke atas atau ke bawah dari anggota lainnya. Semua
anggota keluarga fungsi tersebut mempunyai turunan
yang sama, yaitu 𝑓 𝑥 .
Keluarga fungsi yang turunannya sama
Diketahui fungsi 𝐹 𝑥
dan turunannya.
𝐹 𝑥 𝐹′ 𝑥
𝑥2
+ 2 2𝑥
𝑥2 2𝑥
𝑥2
− 3 2𝑥

5. Anti-turunan dan Integral Tak Tentu

6. Anti-turunan dan Integral Tak Tentu
Apakah setiap anti turunan 𝑓 𝑥 = 2𝑥 berbentuk
𝐹 𝑥 = 𝑥2
+ 𝐶 ?
Jawaban : Iya. Ini menurut Teorema 4.8.B, yang mengatakan
bahwa dua fungsi dengan turunan sama hanya berbeda
dalam konstanta.
Terkait dengan perbendaharaan turunan yang telah kita
pelajari sebelumnya, kita mempunyai beberapa teorema
berikut tentang integral tak tentu.
Teorema 1 (Aturan Pangkat). Jika 𝑟 ∈ ℚ, dan 𝑟 ≠ −1, maka
𝑥 𝑟
𝑑𝑥 =
𝑥 𝑟+1
𝑟 + 1
+ 𝐶
Teorema 2 (Integral Tak Tentu sin x dan cos x)
𝑠𝑖𝑛𝑥 𝑑𝑥 = − cos 𝑥 + 𝐶 dan 𝑐𝑜𝑠𝑥 𝑑𝑥 = 𝑠𝑖𝑛𝑥 + 𝐶

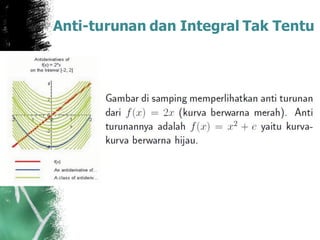
7. Anti-turunan dan Integral Tak Tentu
Teorema 3 (Kelinearan Integral Tak Tentu)
Jika f dan g fungsi dan k adalah konstanta, maka :
i. 𝑘𝑓 𝑥 𝑑𝑥 = 𝑘 𝑓 𝑥 𝑑𝑥 ;
ii. 𝑓 𝑥 + 𝑔 𝑥 𝑑𝑥 = 𝑓 𝑥 𝑑𝑥 + 𝑔 𝑥 𝑑𝑥;
iii. 𝑓 𝑥 − 𝑔 𝑥 𝑑𝑥 = 𝑓 𝑥 𝑑𝑥 − 𝑔 𝑥 𝑑𝑥;
Teorema 4 (Aturan Pangkat yang Diperumum)
Jika 𝑟 ∈ ℚ, 𝑟 ≠ −1, dan g adalah fungsi yang mempunyai
turunan, maka
[𝑔 𝑥 ] 𝑟 𝑔′ 𝑥 𝑑𝑥 =
[𝑔 𝑥 ] 𝑟+1
𝑟 + 1
+ 𝐶
* (𝑎𝑥 + 𝑏)
𝑛
=
1
𝑎(𝑛+1)
(𝑎𝑥 + 𝑏) 𝑛+1

8. Contoh : Anti Turunan Integral
Tak Tentu
1. 𝑥7
+ 5𝑥 28
7𝑥6
+ 5 𝑑𝑥 = ⋯
2. 𝑠𝑖𝑛12
𝑥 𝑐𝑜𝑠𝑥 𝑑𝑥 = ⋯

9. Persamaan Diferensial Sederhana
𝑓 𝑥 𝑑𝑥 = 𝐹 𝑥 + 𝐶
Dalam bahasa diferensial : Jika 𝐹′
𝑥 = 𝑓(𝑥), maka:
𝑑𝐹 𝑥 = 𝐹′ 𝑥 𝑑𝑥 = 𝑓 𝑥 𝑑𝑥
Sehingga
𝑑𝐹 𝑥 = 𝐹 𝑥 + 𝐶
Bentuk ini dinamakan persamaan diferensial. Secara umum,
persamaan diferensial adalah persamaan yang melibatkan
turunan fungsi.

10. Persamaan Diferensial Sederhana
Secara geometris, masalah menyelesaikan persamaan
diferensial
𝑑𝑦
𝑑𝑥
= 𝐹′(𝑥) sama dengan masalah mencari
lengkungan yang garis singgungnya di setiap titik sudah
diberikan.

11. Contoh : Tentukan persamaan kurva yang melalui titik (1,2)
dan mempunyai kemiringannya pada setiap titik pada kurva
sama dengan dua kali absis (koordinat-x) titik tersebut.
Jawab. Misalkan persamaan kurva tersebut adalah y = f(x).
Kondisi yang harus berlaku di setiap titik (𝑥, 𝑦) pada kurva.
Maka, dalam bahasa diferensial, informasi di atas
mengatakan bahwa :
𝑑𝑦
𝑑𝑥
= 2𝑥
𝑑𝑦 = 2𝑥 𝑑𝑥
Integralkan kedua ruas,
Persamaan Diferensial Sederhana
𝑑𝑦 = 2𝑥 𝑑𝑥
𝑦 + 𝐶1 = 𝑥2
+ 𝐶2
𝑦 = 𝑥2
+ 𝐶2 − 𝐶1
𝑦 = 𝑥2
+ 𝐶
Karena kurva melalui titik (1,2), maka
kita memiliki titik 𝑦 = 2 dan 𝑥 = 1 ,
sehingga :
𝑦 = 𝑥2
+ 𝐶
2 = 12
+ 𝐶
𝐶 = 1
Kita simpulkan bahwa 𝐶 = 1, 𝑦 = 𝑥2
+ 𝐶

12. Metode Pemisahan Variabel
Secara umum, tidak ada prosedur baku untuk mencari
solusi persamaan diferensial. Untuk saat ini
pembicaraan akan dibatasi pada persamaan
diferensial yang sangat sederhana. Metode pencarian
solusinya menggunakan metode pemisahan variabel.
Prinsip dari metode ini adalah mengumpulkan semua
suku yang memuat peubah 𝑥 dengan 𝑑𝑥 dan yang
memuat peubah 𝑦 dengan 𝑑𝑦, kemudian diintegralkan.
Selesaikan persamaan diferensial dengan
penyelesaian kedua buah ruas:
𝑑𝑦
𝑑𝑥
=
𝑥 + 3𝑥2
𝑦2
kemudian cari penyelesaian bilamana 𝑥 = 0 dan 𝑦 = 1.

13. Metode Pemisahan Variabel
Pengecekkan akhir pada pekerjaan kita adalah mengganti hasil ini
pada kedua ruas dari persamaan diferensial semula untuk melihat
apakah ia benar. Dengan menggantikan pada ruas kiri, diperoleh :

14. Notasi Jumlah dan Sigma
Penjumlahan deret 𝑛 bilangan 𝑎1 + 𝑎2 + ⋯ + 𝑎 𝑛 dilambang
kan dengan notasi sigma :
𝑖=1
𝑛
𝑎𝑖 = 𝑎1 + 𝑎2 + ⋯+ 𝑎 𝑛
Dengan 𝑎𝑖 ∈ ℝ
Teorema 5 (Kelinearan Sigma)

15. Notasi Jumlah dan Sigma
Beberapa jumlah khusus (dengan indeks i berjalan dari 1
sampai dengan n):
• 𝑖=1
𝑛
𝑖 = 1 + 2 + 3 + ⋯+ 𝑛 =
𝑛(𝑛+1)
2
• 𝑖=1
𝑛
𝑖2
= 1 + 4 + 9 + ⋯+ 𝑛2
=
𝑛(𝑛+1)(2𝑛+1)
6
• 𝑖=1
𝑛
𝑖3
= 1 + 8 + 27 + ⋯ + 𝑛3
=
𝑛(𝑛+1)
2
2
• 𝑖=1
𝑛
𝑖4 = 1 + 4 + 9 + ⋯+ 𝑛2 =
𝑛(𝑛+1)(6𝑛3+9𝑛2+𝑛−1)
6
Contoh : Tentukan nilai dari 𝑖=1
𝑛
[ 𝑖 − 1 4𝑖 + 3 ]

16. Luas Daerah di Bidang
Dalam bentuk sederhana, luas memenuhu lima sifat :
• Luas sebuah daerah rata adalah bilangan (riil) tak negative
• Luas persegi-panjang adalah hasil kali panjang dan lebar
(diukur dalam satuan yang sama)
• Daerah kongruen memiliki luas yang sama
• Luas dari gabungan dua daerah yang hanya berimpit
menurut satu ruas garis sama dengan jumlah luas kedua
daerah tersebut
• Jika satu daerah terkandung di dalam daerah yang kedua,
maka luas daerah pertama kurang dari atau sama dengan
luas yang kedua.

17. Luas Daerah di Bidang
Bila kita meninjau suatu daerah dengan batas
melengkung, masalah penentuan luas menjadi lebih sukar.
Tetapi lebih dari 2000 tahun silam, Archimedes
menyediakan kunci untuk suatu penyelesaian. Katanya,
pandang satu barisan polygon dalam yang menghampiri
daerah melengkung dengan kecermatan yang semakin
besar.

18. Luas Daerah di Bidang

19. Luas Daerah di Bidang

20. Luas Menurut Poligon-Poligon Luar
Luas Menurut Poligon-Poligon Dalam

21. Luas Menurut Poligon-Poligon Luar

22. Luas Menurut Poligon-Poligon Luar
lim
𝑛→∞
𝐿 𝑅 𝑛 =
26
3
Jelas 𝐾 ≤ 𝐿 𝑅 𝑛 sehingga
𝐾 ≤ lim
𝑛→∞
𝐿 𝑅 𝑛 =
26
3

23. Luas Menurut Poligon-Poligon Dalam

24. Luas Menurut Poligon-Poligon Dalam

25. Luas Daerah di Bidang

26. Integral Tentu
Newton dan Leibniz keduanya memperkenalkan versi yang
dini dari konsep integral tentu. Tetapi Riemannlah yang
memberikan kita definisi modern. Dalam perumudan definisi
integral tertentu, dipedomani oleh pemikiran yang dibahas
sebelumnya. Gagasan pertama adalah jumlah Riemaan.

27. Integral Tertentu
Contoh : Halaman 275, Contoh 1 dan 2

28. Definisi Integral Tentu

29. Definisi Integral Tentu
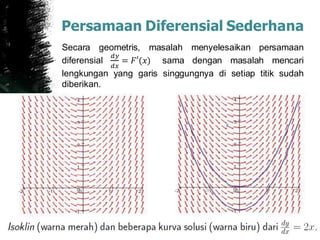
Secara umum, 𝑎
𝑏
𝑓 𝑥 𝑑𝑥 menyatakan batasan luas daerah
yang tercakup diantara kurva 𝑦 = 𝑓(𝑥) dan sumbu-x dalam
selang [𝑎, 𝑏] , yang berarti bahwa tanda positif akan
diberikan pada luas bagian-bagian yang berada di bagian
atas sumbu-x, dan tanda negative diberikan untuk luas
bagian-bagian yang berada di bawah sumbu-x. Secara
simbolik,

30. Sifat-sifat Integral Tentu

31. Sifat-sifat Integral Tentu
Contoh : Halaman 279, Contoh 3 dan 4