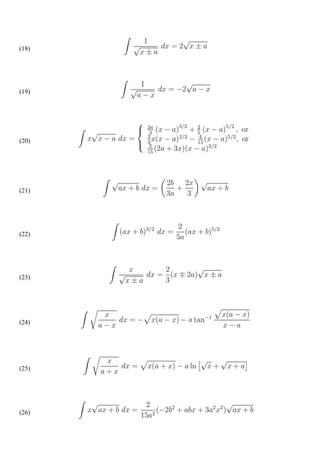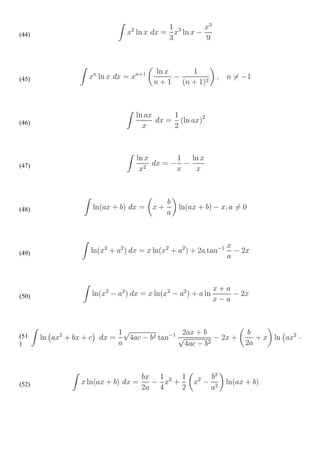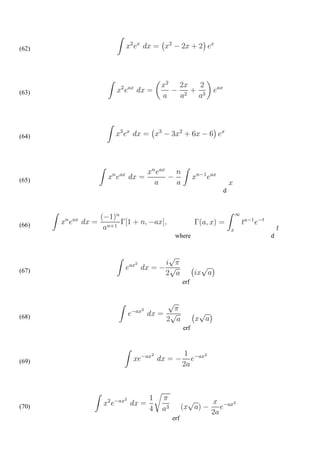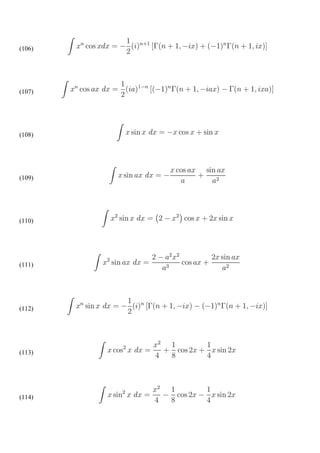Modul 'Persamaan Diferensial 1' karya Maya Umami ini disusun untuk memenuhi tugas akhir mata kuliah dengan 10 bab yang mencakup berbagai jenis persamaan diferensial, dilengkapi dengan contoh soal dan latihan. Penulis berharap modul ini bermanfaat dan memudahkan pemahaman bagi mahasiswa pendidikan matematika. Terima kasih disampaikan kepada dosen pembimbing, Huri Suhendri, M.Pd, atas dukungan dalam penulisan modul ini.

1. Dosen Pembimbing: Huri Suhendri, M.Pd
MODUL
PERSAMAAN DIFERENSIAL 1
OLEH:
Maya Umami (200913500674)
PRODI: PENDIDIKAN MATEMATIKA
SEMESTER: 6 (ENAM) – S6C

2. Assalamuallaikum Wr. Wb
Alhamdulillah modul pada mata kuliah “Persamaan Diferensial 1” ini akhirnya dapat
terselesaikan. Modul ini merupakan tugas akhir atau untuk memenuhi persyaratan (nilai) pada
mata kuliah tersebut. Setelah menjelajahi berbagai literature dan mencoba untuk menemukan
intisari dari materi yang sesuai dengan silabus perkuliahan ini, saya selaku penulis telah
berusaha semaksimal mungkin untuk menemukan intisari yang mudah untuk dipahami
dengan diaadakanya berbagai contoh soal dan latihan-latihan sesuai dengan silabus
perkuliahan.
Syukur ke hadirat Allah SWT penulis panjatkan atas kemudahan yang diberikan-Nya
selama penulisan modul. Tak lupa juga, penulis mengucapkan terima kasih kepada Dosen
Pembimbing kami Bapak Hri Suhendri, M.Pd yang telah memberikan tugas modul ini yang
insyaallah bermanfaat bagi banyak orang terutama bagi penulis.
Modul ini terdiri dari 10 BAB diantaranya: 1. Pendahuluan Persamaan Diferensial; 2.
Persamaan Diferensial Variabel Terpisah; 3. Reduksi ke Bentuk Persamaan Diferensial
Variabel Terpisah; 4. Persamaan Diferensial Homogen; 5. Persamaan Diferensial Tak
Homogen; 6. Persamaan Diferensial Eksak; 7. Reduksi ke Bentuk Persamaan Diferensial
Eksak; 8. Persamaan Diferensial Linier Orde 1; 9. Persamaan Diferensial Bernoulli; 10.
Masalah Nilai Awal (Solusi Khusus). Masing-masing bab dilengkapi oleh materi yang mana
tiap materi diberikan contoh soal dan pembahasan ditambah latihan soal pada bagian akhir
modul ini.
Demikian yang dapat penulis sampaikan. Penulis berharap adanya kritik dan saran
yang membangun guna terciptanya modul yang lebih mendekati kesempurnaan. Semoga
modul ini dapat bermanfaat dan dapat dijadikan modul pegangan pada mata kuliah persamaan
diferensial 1. Amiin….
Wassalamuallaikum Wr. Wb
Jakarta, Juni 2012
- A -

3. KATA PENGANTAR ……………………………………………………. A
DAFTAR ISI ……………………………………………………………… B
BAB 1 PENDAHULUAN PERSAMAAN DIFERENSIAL …………………… 1
1.1. Definisi Persamaan Diferensial ……………………………………. 1
1.2. Bentuk Umum Persamaan Diferensial …………………………….. 1
1.3. Orde (Tingkat) dan Degree (Derajat)………………………………. 1
1.4. Mencari Solusi Persamaan Diferensial …………………………….. 2
1.5. Contoh Soal dan Pembahasan ……………………………………… 2
BAB 2 PERSAMAAN DIFERENSIAL VARIABEL TERPISAH …………… 4
2.1. Persamaan Diferensial Variable Terpisah ………………………….. 4
2.2. Contoh Soal dan Pembahasan ……………………………………… 4
BAB 3 REDUKSI KE BENTUK PERSAMAAN DIFERENSIAL VARIABEL 6
TERPISAH ………………………………………………………………..
3.1. Materi Reduksi ke Bentuk Persamaan Diferensial Variabel 6
Terpisah …………………………………………………………….
3.2. Contoh Soal dan Pembahasan ……………………………………… 6
BAB 4 PERSAMAAN DIFERENSIAL HOMOGEN ………………………….. 8
4.1. Langkah-langkah Menentujan Penyelesaian Umum Persamaan 8
Diferensial Homogen ……………………………………………….
4.2. Contoh Soal dan Pembahasan ……………………………………… 8
- B -

4. BAB 5 PERSAMAAN DIFERENSIAL TAK HOMOGEN …………………… 10
5.1. Persamaan Diferensial dengan M (x,y) dan N (x,y) ……………….. 10
5.2. Contoh Soal dan Pembahasan ……………………………………… 11
BAB 6 PERSAMAAN DIFERENSIAL EKSAK ………………………………. 14
6.1. Sifat-Sifat Dasar ……………………………………………………. 14
6.2. Metode Solusi ……………………………………………………… 14
6.3. Contoh Soal dan Pembahasan ……………………………………… 15
BAB 7 REDUKSI KE BENTUK PERSAMAAN DIFERENSIAL EKSAK 18
(FAKTOR INTEGRASI) …………………………………………………
7.1. Macam-macam faktor integrasi ……………………………………. 18
7.2. Contoh Soal dan Pembahasan ……………………………………… 18
BAB 8 PERSAMAAN DIFERENSIAL LINIER ORDE SATU……………….. 21
8.1. Metode Solusi ……………………………………………………… 21
8.2. Contoh Soal dan Pembahasan ……………………………………… 21
BAB 9 PERSAMAAN DIFERENSIAL BERNOULLI ………………………… 23
9.1. Metode Solusi ……………………………………………………… 23
9.2. Contoh Soal dan Pembahasan ……………………………………… 23
BAB 10 MASALAH NILAI AWAL (SOLUSI KHUSUS) ………………………. 26
10.1. Pengertian ………………………………………………………….. 26
10.2. Contoh Soal dan Pembahasan ……………………………………… 26
LATIHAN SOAL …………………………………………………………. 27
LAMPIRAN ………………………………………………………………. C
DAFTAR PUSTAKA ……………………………………………………. D
- B -

5. BAB
1
1.1. Definisi Persamaan Diferensial
Persamaan Diferensial adalah persamaan yang memuat turunan satu (atau beberapa)
fungsi yang tidak diketahui. Meskipun persamaan seperti itu sehausnya disebut
“persamaan turunan”, namun istilah “persamaan diferensial” (aequatio differentialis)
yang diperkenalkan Leibniz dalam tahun 1676 sudah umum digunakan (Finizio
Ladas:2:1988)
Sebagai contoh:
y’ + xy = 3 ………………………………(1)
y” – 5y’ + 6y = cos x ………………………………(2)
2 2 2
y” = (1+y’ ) (x +y ) ………………………………(3)
𝜕2 𝑢
-
𝜕2 𝑢
=0 ………………………………(4)
𝜕 𝑡2 𝜕𝑥 2
Pada persamaan (1) sampai (3) menyatakan turunan pertama dan kedua dari fungsi y(x)
terhadap x yang disebut persamaan diferensial biasa.
Dalam persamaan (4) memuat turunan-turunan parsial yang disebut persamaan
diferensial parsial.
1.2. Bentuk Umum Persamaan Diferensial
Adapun bentuk umum persamaan diferensial yaitu:
𝑓 𝑥 . 𝑑𝑥 + 𝑔 𝑦 . 𝑑𝑦 = 0
1.3. Orde (Tingkat) dan Degree (Derajat)
Orde (tingkat) adalah turunan tertinggi dalam persamaan diferensial.
Degree (derajat) adalah derajat dari orde tertinggi
Contoh:
Page | 1

6. 2 3
𝑑3 𝑦 𝑑2 𝑦
- + 2xy = 6
𝑑𝑥 3 𝑑𝑥 2
Pada persamaan diatas memiliki orde 3 dan derajat 2.
1.4. Mencari Solusi Persamaan Diferensial
Langkah-langkah:
 Hitunglah banyaknya konstanta sembarang yang ada di dalam persamaan garus
lengkung (kurva) yang akan dicari persamaan diferensialnya.
 Hilangkan semua konstanta sembarang ada n maka untuk mengeliminasi semua
konstanta sembarang itu. Jika banyaknya konstanta sembarang ada n, maka untuk
mengeliminasi semua konstanta sembarang yang ada dubutuhkan n + 1 persamaan.
Untuk mendapatkan n + 1 persamaan, persamaan garis lengkung (kurva) semula
didiferensialkan sampai turunan ke n.
 Banyaknya konstanta sembarang menunjukan orde tertinggi dari turunan dalam
persamaan diferensial yang dicari.
1.5. Contoh Soal dan Pembahasan
1) Carilah persamaan diferensial dari himpunan garis lengkung:
a. y = A sin 2x + B cos 2x ; A dan B adalah konstanta sembarang
b. y = x3 +A x2 + B x + C ; A, B, dan C adalah konstanta sembarang
Pembahasan:
a. Karena ada 2 (dua) konstanta sembarang, maka dibutuhkan 3 persamaan untuk
mengeliminasi A dan B serta orde tertinggi dari turunannya adalah 2.
Persamaan 1 : y = A sin 2x + B cos 2x , turunan terhadap x
𝑑𝑦
Persamaan 2 : = 2A cos 2x – 2B sin 2x, turunan terhadap x
𝑑𝑥
𝑑2 𝑦
Persamaan 3 : = - 4A sin 2x – 4B cos 2x
𝑑𝑥 2
Masukan persamaan (1) ke (3) didapatkan bahwa :
𝑑2 𝑦
= - 4A sin 2x – 4B cos 2x
𝑑𝑥 2
𝑑2 𝑦
= - 4(A sin 2x + B cos 2x)  y = A sin 2x + B cos 2x
𝑑𝑥 2
𝑑2 𝑦
𝑑𝑥 2
= - 4y
𝒅𝟐 𝒚
Jadi, persamaan diferensial yang dicari adalah + 4y = 0
𝒅𝒙 𝟐
Page | 2

7. b. Karena ada 3 (tiga) konstanta sembarang, maka dibutuhkan 4 persamaan untuk
mengeliminasi A dan B serta orde tertinggi dari turunannya adalah 3.
Persamaan 1 : y = x3 +A x2 + B x + C , turunan terhadap x
𝑑𝑦
Persamaan 2 : = 3x2 + 2Ax + B , turunan terhadap x
𝑑𝑥
𝑑2 𝑦
Persamaan 3 : = 6x + 2A , turunan terhadap x
𝑑𝑥 2
𝑑3 𝑦
Persamaan 4 : =6
𝑑𝑥 3
𝑑3 𝑦
Jadi, persamaan diferensial yang dicari adalah =6
𝑑𝑥 3
2) Carilah persamaan diferensial dari berkas kardiola r = a (1-cos 𝜃), a = konstanta
sembarang.
Pembahasan :
Karena ada 1 (satu) konstanta sembarang, maka dibutuhkan 2 persamaan untuk
mengeliminasi A dan B serta orde tertinggi dari turunannya adalah 1.
Persamaan 1 : r = a (1-cos 𝜃) , turunan terhadap x
𝑑𝑟
Persamaan 2 : = a sin 𝜃
𝑑𝜃
𝑟
Dari persamaan (1) didapat a = 1−cos 𝜃
Eliminir a dalam persamaan (2), di dapatkan
𝑑𝑟 𝑟
= 1−cos sin 𝜃
𝑑𝜃 𝜃
Jadi, persamaan diferensialnya adalah: 1 − cos 𝜃 dr – r sin 𝜃 𝑑𝜃 = 0
Page | 3

8. BAB
2
2.1. Persamaan Diferensial Variable Terpisah
Suatu persamaan diferensial variable terpisah ditandai oleh fakta bahwa dua peubah dari
persamaan itu bersama-sama masing-masing didiferensianya, dapat ditempatkan di ruas
yang berlawanan.
Dengan manipulasi aljabar, memunkinkan kita menuliskan persamaan diferensial
terpisah dalam bentuk implisit :
𝑃(𝑥)
y’ = , atau
𝑄 (𝑥)
dalam bentuk eksplisit :
𝑑𝑦 𝑃(𝑥)
=
𝑑𝑥 𝑄 (𝑥)
Untuk memperoleh penyelesaian umum suatu persamaan diferensial terpisah, pertama-
tama kita pisahkan kedua peubah dan kemudian integralkan kedua ruas.
Awal  Q (y) dy = P (x) dx
Integral  P (x) dx = Q (y) dy + C dimana C = Konstanta sembarang
Note: bisa dilakukan hanya pada variable yang sama. Contoh :
Hanya mengandung 𝑦+1 Hanya mengandung
 dy = -x dx 
𝑦 2 +4
variable y variable x
2.2. Contoh Soal dan Pembahasan
Selesaikan setiap persamaan diferensial di bawah ini:
1) y2 dy = (x + 3x2) dx , bilamana x = 0 dan y = 6  bentuk eksplisit
2) xyy’ + x2 + 1 = 0  bentuk implisit
Page | 4

9. Pembahasan:
1) y2 dy = (x + 3x2) dx , syarat harus mengandung variable yang sama pada tiap ruas.
 Integralkan kedua ruas
y 2 dy = (x + 3x 2 ) dx
𝑦3 𝑥2
+C1 = + x 3 + C2
3 2
3𝑥 2
y3 = + 3x 3 + (3C2 – 3C1)
2
3𝑥 2
= + 3x 3 + C ; C = 3C2 – 3C1
2
3 3𝑥 2
y = + 3x 3 + C
2
3 3𝑥 2
 Maka, solusi umumnya adalah: = + 3x 3 + C
2
 Menghitung konstanta C, kita menggunakan persyaratannya bilamana x = 0 dan
y = 6, maka akan menghasilkan:
3
6= 𝐶
C = 216
3 3𝑥 2
 Solusi khususnya adalah: y = + 3x 3 + 216
2
2) xyy’ + x2 + 1 = 0
 Ubah ke dalam eksplisit
𝑑𝑦
xy + x2 + 1 = 0
𝑑𝑥
 Bagi tiap-tiap ruas
x2 + 1
y dy = − dx
𝑥
 Integralkan masing-masing ruas
x2 + 1
y dy =− dx
𝑥
𝑦2 1
+C =− 𝑋+ dx
2 𝑥
𝑦2 x2
+C =− + 𝐿𝑛 |𝑥| + C
2 2
𝑦2 = − x 2 − 2 𝐿𝑛 𝑥 + 𝑐
y = − x 2 − 2 𝐿𝑛 𝑥 + 𝑐
 Maka, solusi umumnya adalah:
y = − x 2 − 2 𝐿𝑛 𝑥 + 𝑐
Page | 5

10. BAB
3
3.1. Materi Reduksi ke Bentuk Persamaan Diferensial Variabel Terpisah
Tidak semua persamaan diferensial mudah untuk didapatkan solusinya. Pada saat
persamaan diferensial memiliki bentuk:
f1 (x) g1 (y) dx ± f2 (x) g2 (y) dy
1
Maka dibutuhkan reduksi dengan menggunakan faktor integrasi , yang
g1 y F2 (x)
kemudian akan menjadi:
f1 (x) g1 (y)
dx ± dy =0
f2 (x) g2 (y)
f1 (x) g1 (y)
dx = ± dy
f2 (x) g2 (y)
Pengitegralan masing-masing ruas:
f1 (x) g1 (y)
dx = ± dy
f2 (x) g2 (y)
3.2. Contoh Soal dan Pembahasan
Tentukan solusi umum dari persamaan diferensial berikut:
1) (x3y + yx2) dx + (y3x2 + 2x2y) dy = 0
2) (x2-1) dx – (2x+xy) dy = 0
Pembahasan
1) (x3y + yx2) dx + (y3x2 + 2x2y) dy = 0
y (x3 + x2) dx + x2 (x2 + 2y) dy = 0
1
faktor integrasi : yx 2
Page | 6

11. 1
[y (x3 + x2) dx + x2 (x2 + 2y) dy] = 0
yx 2
(x3 + x2) dx + (x2 + 2y) dy = 0
Karena sudah memiliki variable yang sama, langkah selanjutnya adalah integralkan.
(x3 + x2) dx + (x2 + 2y) dy = 0
𝑥4 𝑥3 𝑦4
+ + + 𝑦2 + C = 0
4 3 4
x 12
3x4 + 4x3 + 3y4 + 12 y2 = C
Maka, Solusi umumnya adalah 3x4 + 4x3 + 3y4 + 12 y2 = C
2) (x2-1) dx – (2x+xy) dy = 0
(x2-1) dx – x (2+y) dy = 0
1
faktor integrasi : 𝑥
1
[(x2-1) dx – x (2+y) dy] = 0
𝑥
x 2 −1
dx – (2+y) dy = 0
𝑥
x 2 −1
dx – (2+y) dy = 0
𝑥
𝑥2 𝑦2
-Ln |x| - 2y - =0
2 2
x2
𝑥 2 - 2 Ln |x| - 4y - 𝑦 2 = 0
𝑥 2 - 𝑦 2 - 2 Ln |x| - 4y = 0
Maka, solusi umumnya adalah 𝑥 2 - 𝑦 2 - 2 Ln |x| - 4y = 0
Page | 7

12. BAB
4
f (x,y) dikatakan homogen berderjat n jika:
f (𝛼x,𝛼y) = 𝛼 n f (x,y)
M (x,y) dx + N (x,y) dy = 0
Syarat persamaan diferensial diatas dikatakan homogeny jika M (x,y) dan N (x,y) adalah
homogeny dan berderajat sama.
4.1. Langkah-langkah Menentujan Penyelesaian Umum Persamaan Diferensial
Homogen
 Gunakan tranformasi:
y = u x  dy = x du + u dx, atau
x = u y  dy = y dy + u du
 Persamaan diferensial homogeny tereduksi ke Persamaan Diferensial terpisah
 Gunakan aturan persamaan diferensial terpisah untuk mendapatkan solusi umum
persamaan diferensial.
𝑦 𝑥
 Gantilah u = jika menggunakan transformasi y = u x, dan u = jika menggunakan
𝑥 𝑦
transformasi x = u y untuk mendapatkan kembali variable semula.
4.2. Contoh Soal dan Pembahasan
Buktikan bahwa persamaan tersebut adalah persamaan homogen!
𝑥3+ 𝑦3
1) y’ = 𝑥𝑦 2
2) (2x2y + y3) dx + (xy2 – 2x3) dy = 0
Pembahasan:
𝑥3+ 𝑦3 𝑑𝑦 𝑥3+ 𝑦 3
1) y’ =  =
𝑥𝑦 2 𝑑𝑥 𝑥𝑦 2
xy2 dy – (x3+y3) dx = 0
Page | 8

13.  fungsi M (x,y) dx
M (x,y) dx = -x3-y3  = - 𝛼 3 𝑥 3 - 𝛼 3 𝑦 3
= 𝛼 3 (−𝑥 3 −𝑦 3 )
M (𝛼x,𝛼y) = 𝛼 3 [M (x,y)]
 fungsi N (x,y) dy
N (x,y) dy = xy2  = 𝛼𝑥𝛼 3 𝑦 3
= 𝛼 3 (x𝑦 2 )
N (𝛼x,𝛼y) = 𝛼 3 [N (x,y)]
 didapatkan 𝛼 3 , maka TERBUKTI persamaan diferensial diatas merupakan
persamaan diferensial homogeny berderajat 3.
2) (2x2y + y3) dx + (xy2 – 2x3) dy = 0
 fungsi M (x,y) dx
M (x,y) dx = 2x2y + y3  = 2𝛼 2 x2 𝛼 y + 𝛼 3 y3
= 𝛼 3 (2x2y + y3)
M (𝛼x,𝛼y) = 𝛼 3 [M (x,y)]
 fungsi N (x,y) dy
N (x,y) dy = xy2 – 2x3  = 𝛼 x𝛼 2 y2 – 2𝛼 3 x3
= 𝛼 3 (xy2 – 2x3)
N (𝛼x,𝛼y) = 𝛼 3 [N (x,y)]
 didapatkan 𝛼 3 , maka TERBUKTI persamaan diferensial diatas merupakan
persamaan diferensial homogeny berderajat 3.
Page | 9

14. BAB
5
5.1. Persamaan Diferensial dengan M (x,y) dan N (x,y)
Persamaan ini merupakan persamaan linier tetapi tidak homogen. Pandang bentuk
persamaan diferensial dibawah ini:
( ax + by + c ) dx + ( px + qy + r ) dy = 0
Dimana a,b,c,p,q,r merupakan suatu konstanta.
Ada 3 (tiga) kemungkinan yang dapat terjadi:
𝑎 𝑏 𝑐
1) = 𝑞= 𝑟= 𝛼
𝑝
Langkah-langkah penyelesaian:
𝑎 𝑏 𝑐
Karena = = = 𝛼 , maka menggunakan transformasi px + qy + r = u, yang berarti
𝑝 𝑞 𝑟
bahwa ax + by + c = 𝛼u
Bentuk persamaan tereduksi menjadi persamaan dengan variable terpisah dan
kemudian selesaikanlah.
𝑎 𝑏 𝑐
2) = 𝑞≠
𝑝 𝑟
Langkah-langkah penyelesaian:
𝑑𝑢 −𝑞 𝑑𝑦
Gunakan transformasi px + qy = u, dan dari sini berarti dy = , atau
𝑞
𝑑𝑢 −𝑞 𝑑𝑦
dx= 𝑝
𝑎 𝑏
Misalkan 𝑝 = 𝑞 = 𝛽, maka ax + by = 𝛽 u
Persamaan tereduksi menjadi persamaan variable terpisah.
𝑑𝑢 −𝑝 𝑑𝑥 𝑑𝑢 −𝑝 𝑑𝑥
(𝛽 x + C) dx + (u + r) = 0, atau (𝛽 x + C) + (u + r) 𝑑𝑦 = 0
𝑞 𝑞
Selesaikan persamaan variable terpisah ini dan kemudian gantilah x = px + qy untuk
mendapatkan solusi umumnya.
Page | 10

15. 𝑎 𝑏
3) ≠
𝑝 𝑞
Langkah-langkah penyelesaian:
 Gunakan Transformasi
ax + by + c = u  a dx + b dy = du
px + qy + r = v  p dx + q dy = dv
dari dua persamaan diatas diperoleh bahwa:
𝑞 𝑑𝑢 −𝑏 𝑑𝑣 𝑎 𝑑𝑢 −𝑝 𝑑𝑣
dx = , dan dy =
𝑎𝑞 −𝑏𝑝 𝑎𝑞 −𝑏𝑝
selesaikan persamaan diferensial diatas dan kemudian gantilah kembali u dan v
dengan tranformasi semula untuk mendapatkan solusi umum persamaan
diferensial semula.
5.2. Contoh Soal dan Pembahasan
Tentukan solusi umum persamaan diferensial dibawah ini!
1) (2x – 5y +2) dx + (10y – 4x – 4) dy = 0
𝑑𝑦 1−2𝑦−4𝑥
2) =
𝑑𝑥 1+𝑦+2𝑥
𝑑𝑦 6𝑥−2𝑦−7
3) = 2𝑥+3𝑦−6
𝑑𝑥
Pembahasan:
1) (2x – 5y +2) dx + (10y – 4x – 4) dy = 0
a b c q p r
𝑎 2 1 𝑏 −5 1 𝑐 2 1
= −4 = - 2 ; = 10 = - 2 ; = −4 = - 2
𝑝 𝑞 𝑟
𝑎 𝑏 𝑐 1
Maka, = = = 𝛼 = -
𝑝 𝑞 𝑟 2
Penyelesaian:
 px + qy + r = u
ax + by + c = 𝛼 u
1
=-2u
 (2x – 5y +2) dx + (10y – 4x – 4) dy = 0
1
-2u dx + u dy = 0
xu
1
-2 dx + dy = 0
Page | 11

16. 1
-2 dx + dy =0
1
-2x +y=C
1
Maka Solusi umumnya adalah - 2 x + y = C
𝑑𝑦 1−2𝑦−4𝑥
2) =
𝑑𝑥 1+𝑦+2𝑥
(1 − 2𝑦 − 4𝑥) dx = (1 + 𝑦 + 2𝑥) dy = 0
c b a r q p
𝑎 −4 𝑏 −2 𝑐 −7
= −2 = 2 ; = −1 = 2 ; =
𝑝 𝑞 𝑟 6
Maka,
𝑎 𝑏 𝑐
≠ = 𝛽=2
𝑝 𝑞 𝑟
Penyelesaian:
 px + qy = u  ax + by = 𝛽 u
-2x+(-y) = u -4x – 2y = 2u
-2x – y = u
 Pengganti dx atau dy
-2x –y = u  -2x –y = u
𝑢 +𝑦
x = y = - (u + 2x)
−2
𝑑𝑢 +𝑑𝑦 dy = - du – 2dx
dx = −2
 Solusi umum
(1 − 2𝑦 − 4𝑥) dx = (1 + 𝑦 + 2𝑥) dy = 0
𝑑𝑢 +𝑑𝑦
(1 – 2u) - (1 – u) dy = 0
−2
x2
(1 – 2u) (𝑑𝑢 + 𝑑𝑦) - 2 (1 – u) dy = 0
du + dy + 2udu + 2udy – 2dy + 2udy = 0
du – dy + 2 udu + 4udy = 0
(1 + 2u) du + (4u – 1) dy = 0
: (4u – 1)
1+2𝑢
du + dy = 0
4𝑢−1
Page | 12

17. 1+2𝑢
du + dy = 0
4𝑢−1
1 2𝑢
du + du + dy = 0
4𝑢−1 4𝑢−1
Ln |4𝑢 − 1| + 2u Ln |4𝑢 − 1| + y = C
 Maka, solusi umumnya adalah: Ln |4𝑢 − 1| + 2u Ln |4𝑢 − 1| + y = C
𝑑𝑦 6𝑥−2𝑦−7
3) = 2𝑥+3𝑦−6
𝑑𝑥
(6𝑥 − 2𝑦 − 7) dx – (2𝑥 + 3𝑦 − 6) dy = 0
a b c p q r
maka didapatkan
𝑎 6 𝑏 −2 2 𝑐 1
= −2 = - 3 ; = −3 = 3 ; = −1 = -1
𝑝 𝑞 𝑟
𝑎 𝑏
≠
𝑝 𝑞
Penyelesaian:
(qu – pv) du + (qv – bu) dv = 0
(-3u + 2v) du + (bv + 2u) dv = 0  Persamaan Diferensial Homogen
Subtitusi:
𝑢
z = 𝑣 , atau u = zv  du = v dz + z dv
Solusi Umum:
(-3u + 2v) du + (bv + 2u) dv = 0
(-3 zv + 2v) (v dz + z dv) + (bv + 2 zv) dv = 0
v2 (-3z + 2) dz + v (-3z2 + 4z + 6) dv = 0
: v2 (-3z + 2)
−3𝑧+2
dz + v dv = 0
−3z2 + 4z + 6
−3𝑧+2
dz + v dv = 0
−3z2 + 4z + 6
−3𝑧 2 1
dz + dz + 2 v2 dv = 0
−3z2 + 4z + 6 −3z2 + 4z + 6
1
−3𝑧 𝐿𝑛 | − 3z2 + 4z + 6| + 2 𝐿𝑛 | − 3z2 + 4z + 6| + 2 v2 dv = C
x2
2
−6𝑧 𝐿𝑛 | − 3z2 + 4z + 6| + 4 𝐿𝑛 | − 3z2 + 4z + 6| + v dv = C
Maka, Solusi Umumnya adalah:
−6𝑧 𝐿𝑛 | − 3z2 + 4z + 6| + 4 𝐿𝑛 | − 3z2 + 4z + 6| + v2 dv = C
Page | 13

18. BAB
6
6.1. Sifat-Sifat Dasar
Suatu persamaan diferensial dengan bentuk:
M (x,y) dx + N (x,y) dy = 0
Dikatakan persamaan diferensial eksak, jika ada suatu fungsi f(x,y) yang diferensial
totalnya sama dengan M (x,y) dx + N (x,y) dy, yaitu (dengan meniadakan lambang
x dan y):
df = M dx + N dy
uji kepastian : Jika M dan N merupakan fungsi kontinu dan memiliki turunan
parsial pertama yang kontinu pada sebuah segiempat bidang xy,
𝜕𝑀 𝜕𝑁
maka M (x,y) dx + N (x,y) dy = 0 adalah eksak hanya jika: =
𝜕𝑦 𝜕𝑥
6.2. Metode Solusi
Untuk menentukan solusi dari M (x,y) dx + N (x,y) dy = 0, maka secara implicit
diberikan oleh penyelesaian umum f (x,y) = c.
Langkah-langkah menemukan suatu fungsi f (x,y) adalah:
 Langkah 1
Perhatikan bahwa:
𝜕𝑓 𝜕𝑓
= M (x,y), dan = N (x,y)
𝜕𝑥 𝜕𝑦
 Langkah 2
Integrasikan (mencari integral) dari M (x,y) terhadap x dengan y tetap.
𝜕𝑓
dx = M (x,y) dx
𝜕𝑥
𝑥
f (x,y) = [ M (x, y) dx ] + ∅(𝑦)
dimana ∅𝑦 adalah fungsi sembarang dari y saja.
 Langkah 3
Fungsi f (x,y) pada langkah ke-2, didiferensialkan parsial terhadap y yang
selanjutnya akan diperoleh:
Page | 14

19. 𝜕𝑓 𝜕 𝑥 𝜕∅
= [ M (x, y) dx ] +
𝜕𝑦 𝜕𝑦 𝜕𝑦
 Langkah 4
𝜕𝑓
Karena = N (x,y) maka,
𝜕𝑦
𝜕∅ 𝜕 𝑥
= N (x,y) - [ M (x, y) dx ]
𝜕𝑦 𝜕𝑦
Dari sini ∅(𝑦) akan diperoleh.
 Langkah 5
∅(𝑦) yang baru saja diperoleh, disubtitusikan ke f (x,y) dalam langkaj ke-2.
Dengan demikian f (x,y) = C dapat diperoleh.
6.3. Contoh Soal dan Pembahasan
Tentukan solusi umum dari persamaan diferensial di bawah ini dan buktikan
keeksakanya!
1) (2xy + x2) dx + (x2 + y2) dy = 0
2) 3x2y2 dx + (2x3y + 4y3) dy = 0
Pembahasan:
1) (2xy + x2) dx + (x2 + y2) dy = 0
 Pembuktian Persamaan Diferensial Eksak
𝜕𝑀
M (x, y) = 2xy + x2  = 2𝑥
𝜕𝑦
𝜕𝑁
N (x, y) = x2 + y2  = 2𝑥
𝜕𝑥
𝜕𝑀 𝜕𝑁
Karena = , maka persamaan diferensial diatas merupakan persamaan
𝜕𝑦 𝜕𝑥
diferensial eksak.
 Mencari Solusi Umum
Langkah 2 (mencari f (x,y))
𝑥
f (x,y) =[ M (x, y) dx ] + ∅(𝑦)
𝑥
= (2xy + x2) dx + ∅(𝑦)
1
= x2y + 3 x3 + ∅(𝑦)
Page | 15

20. Langkah 3
𝜕𝑓 𝜕 𝑥 𝜕∅
= [ M (x, y) dx ] +
𝜕𝑦 𝜕𝑦 𝜕𝑦
𝜕 𝑥 𝜕∅
= [ (2xy + x2) dx ] +
𝜕𝑦 𝜕𝑦
𝜕
= x2 + ∅(𝑦)
𝜕𝑦
Langkah 4 (mencari ∅(𝑦))
𝜕𝑓
= N (x,y)
𝜕𝑦
𝜕
x2 + ∅(𝑦) = x2 + y2
𝜕𝑦
𝜕
∅(𝑦) = x2 + y2 - x2
𝜕𝑦
∅(𝑦) = y 2 dy
1
= y3 + k
3
Langkah 5 (Solusi Umum)
1
f (x,y) = x2y + 3 x3 + ∅(𝑦)
1 1
= x2y + 3 x3 + 3 y 3 = k
x3
= 3x y + x + y 3 = 3k
2 3
Maka solusi umumnya adalah 3x2y + x3 + y 3 = C dengan nilai C=3k
2) 3x2y2 dx + (2x3y + 4y3) dy = 0
 Pembuktian Persamaan Diferensial Eksak
𝜕𝑀
M (x, y) = 3x2y2  = 6𝑥 2 𝑦
𝜕𝑦
𝜕𝑁
N (x, y) = 2x3y + 4y3  = 6𝑥 2 𝑦
𝜕𝑥
𝜕𝑀 𝜕𝑁
Karena = , maka persamaan diferensial diatas merupakan persamaan
𝜕𝑦 𝜕𝑥
diferensial eksak.
 Mencari Solusi Umum
Langkah 2 (mencari f (x,y))
𝑥
f (x,y) =[ M (x, y) dx ] + ∅(𝑦)
𝑥
= 3x 2 y 2 dx + ∅(𝑦)
= x3y2+ ∅(𝑦)
Page | 16

21. Langkah 3
𝜕𝑓 𝜕 𝑥 𝜕∅
= [ M (x, y) dx ] +
𝜕𝑦 𝜕𝑦 𝜕𝑦
𝜕 𝑥 𝜕∅
= [ 3x 2 y 2 dx ] +
𝜕𝑦 𝜕𝑦
𝜕
= 2x3y + ∅(𝑦)
𝜕𝑦
Langkah 4 (mencari ∅(𝑦))
𝜕𝑓
= N (x,y)
𝜕𝑦
𝜕
2x3y + ∅(𝑦) = 2x3y + 4y3
𝜕𝑦
𝜕
∅(𝑦) = 2x3y + 4y3 - 2x3y
𝜕𝑦
∅(𝑦) = 4y 3 dy
= y4 + k
Langkah 5 (Solusi Umum)
f (x,y) = x3y2+ ∅(𝑦)
= x3y2+ y 4 = k
Maka solusi umumnya adalah x3y2+ y 4 = C dengan nilai C = k
Page | 17

22. BAB
7
Secara umum persamaan M (x,y) dx + N (x,y) dy = 0 tidak eksak. Terkadang adalah mungkin
mengubah menjadi persamaan diferensial eksak melalui perkalian yang eksak.
Oleh karena itu, fungsi untuk mengubah Persamaan Diferensial tiadk eksak ke bentuk
persamaan diferensial eksak adalah factor integrasi (Faktor pengkali/ Gabung).
7.1. Macam-macam faktor integrasi
Ada beberapa macam faktor integrasinya, yaitu:
𝜕𝑀 𝜕𝑁
−
𝜕𝑦 𝜕𝑥
 Jika, = f(x) dimana f(x) merupakan fungsi dari x saja
𝑁
f x dx
Faktor Integrasinya: 𝑒
𝜕𝑀 𝜕𝑁
−
𝜕𝑦 𝜕𝑥
 Jika, = g(y) dimana g(y) merupakan fungsi dari y saja
−𝑀
g y dy
Faktor Integrasinya: 𝑒
 Jika, M (x,y) dx + N (x,y) dy = 0 merupakan Persamaan Diferensial Homogen dan
xM + yN ≠ 0
1
Faktor Integrasinya: xM + yN
 Jika, M (x,y) dx + N (x,y) dy = 0 dapat diubah ke bentuk
y f(x,y) dx + x g(x,y) dy = 0 dan f(x,y) ≠ g(x,y)
1
Faktor Integrasinya: xM − yN
 Dan sebagainya
7.2. Contoh Soal dan Pembahasan
Tentukan Faktor Integrasi kemudian tentukan solusi umumnya!
1) 3x2y2 dx + (4x3y – 12) dy = 0
2) (2y – x3) dx + x dy = 0
Page | 18

23. Pembahasan:
1) 3x2y2 dx + (4x3y – 12) dy = 0
𝜕𝑀
M = 3x2y2  = 6x2y
𝜕𝑦
𝜕𝑀
N = 4x3y – 12  = 12x2y
𝜕𝑦
𝜕𝑀 𝜕𝑁
Karena ≠ maka, bukan merupakan persamaan diferensial eksak
𝜕𝑦 𝜕𝑥
𝜕𝑀 𝜕𝑁
− 16𝑥 2 𝑦 −12𝑥 2 𝑦 −2 4 2
𝜕𝑦 𝜕𝑥
 = = + =
−𝑀 −3𝑥 2 𝑦 2 𝑦 𝑦 𝑦
2
g y dy dy
Faktor Integrasi: 𝑒 = 𝑒 𝑦 = 𝑒 2 ln 𝑦 = y2
 Faktor Integrasi f(x)
y2 [3x2y2 dx + (4x3y – 12) dy] = 0
3x2y4 dx + (4x3y3 – 12 y2) dy = 0
𝜕𝑀
M = 3x2y4  = 12x2y3
𝜕𝑦
𝜕𝑀
N = 4x3y3 – 12 y2  = 12x2y3
𝜕𝑦
𝜕𝑀 𝜕𝑁
Karena = maka, merupakan persamaan diferensial eksak
𝜕𝑦 𝜕𝑥
 Solusi Umum
Mencari f(x,y) dengan mengintegralkan M
𝑥
f (x,y) =[ M (x, y) dx ] + ∅(𝑦)
𝑥
= 3x 2 y 4 dx + ∅(𝑦)
= x3y4+ ∅(𝑦)
Mencari ∅(𝑦) dengan mendiferensialkan f(x,y) = N
𝜕𝑓
= N (x,y)
𝜕𝑦
𝜕
4x3y3 + ∅(𝑦) = 4x3y3 – 12 y2
𝜕𝑦
𝜕
∅(𝑦) = 4x3y3 – 12 y2 - 4x3y3
𝜕𝑦
∅(𝑦) = − 12 y 2 dy
= - 4 y3 + k
Masukan ke persamaan f(x,y)
f (x,y) = x3y4+ ∅(𝑦)
= x3y4 − 4 y 3 = k
Maka solusi umumnya adalah x3y4 − 4 y 3 = C dengan nilai C = k
Page | 19

24. 2) (2y – x3) dx + x dy = 0
𝜕𝑀
M = 2y – x3  =2
𝜕𝑦
𝜕𝑀
N=x  =1
𝜕𝑦
𝜕𝑀 𝜕𝑁
Karena ≠ maka, bukan merupakan persamaan diferensial eksak
𝜕𝑦 𝜕𝑥
𝜕𝑀 𝜕𝑁
− 2−1 1
𝜕𝑦 𝜕𝑥
 = =
𝑁 𝑥 𝑥
1
f x dy dx
Faktor Integrasi: 𝑒 = 𝑒 𝑥 = 𝑒 ln 𝑥 = x
 Faktor Integrasi f(x)
x [(2y – x3) dx + x dy] = 0
(2xy – x4) dx + x2 dy = 0
𝜕𝑀
M = 2xy – x4  = 2x
𝜕𝑦
𝜕𝑀
N = x2  = 2x
𝜕𝑦
𝜕𝑀 𝜕𝑁
Karena = maka, merupakan persamaan diferensial eksak
𝜕𝑦 𝜕𝑥
 Solusi Umum
Mencari f(x,y) dengan mengintegralkan M
𝑥
f (x,y) =[ M (x, y) dx ] + ∅(𝑦)
𝑥
= (2xy – x 4 ) dx + ∅(𝑦)
1
= x2y − 5 x 5 + ∅(𝑦)
Mencari ∅(𝑦) dengan mendiferensialkan f(x,y) = N
𝜕𝑓
= N (x,y)
𝜕𝑦
𝜕
x2 + ∅(𝑦) = x2
𝜕𝑦
𝜕
∅(𝑦) = x2 – x2
𝜕𝑦
∅(𝑦) = 0 dy
= k
Masukan ke persamaan f(x,y)
1
f (x,y) = x2y − 5 x 5 + ∅(𝑦)
1
= x2 y − x 5 = k
5
1
Maka solusi umumnya adalah x2y − 5 x 5 = C dengan nilai C = k
Page | 20

25. BAB
8
8.1. Metode Solusi
Persamaan linier orde satu memiliki bentuk umum
𝑑𝑦
+ P(x) y = Q(x) dengan syarat ruas kanan ≠ 0
𝑑𝑥
P x dx
Factor integrasi: 𝑒
Solusi umum
P x dx P x dx
𝑒 y= Q(x) 𝑒 + 𝐶
8.2. Contoh Soal dan Pembahasan
Tentukan solusi umum dari:
𝑑𝑦
1) + 4y = x -2x2
𝑑𝑥
2) 𝑦 ′ + 𝑦 = (1 + 𝑥)2
Pembahasan:
𝑑𝑦
1) + 4y = x -2x2
𝑑𝑥
P(x) = 4 ; Q(x) = x – 2x2
P x dx 4 dx
Faktor Integrasi: 𝑒 = 𝑒 = 𝑒 4𝑥
Solusi Umum:
P x dx P x dx
𝑒 y= Q(x) 𝑒 + 𝐶
𝑒 4𝑥 y = x – 2x 2 𝑒 4𝑥 + 𝐶
𝑥−2𝑥 2 1−4𝑥 1 𝑐
y= − − +
4 16 16 𝑒 4𝑥
4𝑥−8𝑥 2 −1+4𝑥−1 𝑐
y= +
16 𝑒 4𝑥
4𝑥−4𝑥 2 −1 𝑐
y= +
8 𝑒 4𝑥
Page | 21

26. 2) 𝑦 ′ + 𝑦 = (1 + 𝑥)2
𝑑𝑦
+ 𝑦 = (1 + 𝑥)2
𝑑𝑥
P(x) = 1 ; Q(x) = (1 + 𝑥)2
P x dx 1 dx
Faktor Integrasi: 𝑒 = 𝑒 = 𝑒𝑥
Solusi Umum:
P x dx P x dx
𝑒 y= Q(x) 𝑒 + 𝐶
𝑒 𝑥 y = (1 + 𝑥)2 𝑒 𝑥 + 𝐶
𝑒 𝑥 y = 𝑒 𝑥 (1 + 𝑥)2 − 2𝑒 𝑥 (1 + 𝑥) + 2𝑒 𝑥 + C
2 𝑐
y=[ 1+ 𝑥 −2 1+ 𝑥 +2+ 𝑒𝑥
Page | 22

27. BAB
9
9.1. Metode Solusi
 Bentuk umum dari persamaan diferensial Bernoulli adalah:
𝑑𝑦
+ P(x) y = Q(x) yn
𝑑𝑥
 Persamaan Bernoulli akan tereduksi ke persamaan linier orde satu dengan
Transformasi:
z = y-n+1
𝑑𝑧 𝑑𝑦
= (-n + 1) y-n.
𝑑𝑥 𝑑𝑥
𝑑𝑦 𝑑𝑧
= (1 – n) yn.
𝑑𝑥 𝑑𝑥
 Persamaan linier orde satu
𝑑𝑧
= (1 – n) P(x) y-n = (1 – n) Q(x)
𝑑𝑥
𝑑𝑧
= (1 – n) P(x) z = (1 – n) Q(x)
𝑑𝑥
1 – n P x dx
Dengan faktor integrasi: 𝑒
 Solusi umum
1 – n P x dx 1 – n P x dx
𝑒 z = (1 – n) Q(x) 𝑒 𝑑𝑥 + C
9.2. Contoh Soal dan Pembahasan
Cari solusi dari:
𝑑𝑦 𝑦 𝑦2
1) + 𝑥=
𝑑𝑥 𝑥
𝑑𝑦
2) + y = xy3
𝑑𝑥
Pembahasan:
𝑑𝑦 𝑦 𝑦2
1) + 𝑥=
𝑑𝑥 𝑥
1 1
P(x) = 𝑥
; Q(x) = 𝑥
;n=2
Page | 23

28. z = y-n+1
z = y-2+1
z = y-1
𝑑𝑧 𝑑𝑦
= - y-2.
𝑑𝑥 𝑑𝑥
𝑑𝑦 𝑑𝑧
= - y2.
𝑑𝑥 𝑑𝑥
𝑑𝑦 𝑦 𝑦2
+ 𝑥=
𝑑𝑥 𝑥
𝑑𝑧 𝑦 𝑦2
- y2. + =
𝑑𝑥 𝑥 𝑥
: - y2
𝑑𝑧 1 1
- 𝑦 −1 = −
𝑑𝑥 𝑥 𝑥
𝑑𝑧 1 1
- 𝑥− 𝑧=−  Persamaan Linier Orde Satu
𝑑𝑥 𝑥
1 1
P(x) = − ; Q(x) = −
𝑥 𝑥
solusi umum:
1 – n P x dx 1 – n P x dx
𝑒 z = (1 – n) Q(x) 𝑒 𝑑𝑥 + C
1 1 1
z= − 𝑑𝑥 + C
𝑥 𝑥 𝑥
1
z = 𝑥 −1 + C
𝑥
𝑥 −1 + 𝐶
𝑧=
1
𝑥
1
Maka, Solusi Umumnya adalah 𝑦 = 1 + Cx
𝑑𝑦
3) + y = xy3
𝑑𝑥
P(x) = 1 ; Q(x) = xy3 ;n=3
z = y-n+1
z = y-3+1
z = y-2
𝑑𝑦 1 𝑑𝑧
=
𝑑𝑥 𝑛−1 𝑑𝑥
𝑑𝑦 1 𝑑𝑧
=
𝑑𝑥 −2 𝑑𝑥
Persamaan Diferensial Orde Satu
𝑑𝑧
+ (1 – n) z p(x) = (1 – n) Q(x)
𝑑𝑥
Page | 24

29. 𝑑𝑧
+ -2y-2 = -2x
𝑑𝑥
Solusi Umum:
1 – n P x dx 1 – n P x dx
𝑒 z = (1 – n) Q(x) 𝑒 𝑑𝑥 + C
−2 dx −2 dx
𝑒 y-2 = −2x 𝑒 𝑑𝑥
−2𝑥 𝑦 −2 = 4x 2 dx
4
−2𝑥 𝑦 −2 = 𝑥3 + k
3
x3
−6𝑥 𝑦 −2 = 4𝑥 3 + 3k
6𝑥 𝑦 −2 + 4𝑥 3 = C
Maka, Solusi umumnya adalah 6𝑥 𝑦 −2 + 4𝑥 3 = C ; C =3k
Page | 25

30. BAB
10
10.1. Pengertian
Soal Nilai Awal merupakan suatu persamaan diferensial bersama dengan kondisi-
kondisi tambahan terhadap fungsi yang dicari dan turunannya yang semuanya diberikan
pada nilai variable independen yang sama. Masalah Nilai awal adalah mencari solusi
khusus dari kondisi awal. Solusi khusus adalah ketika persamaan diferensial hanya
memiliki satu solusi saja. Misalnya (y’)4 + y2 = 0. Persamaan ini hanya memiliki satu
solusi yaitu y = 0. Dan tidak mengandung nilai C
10.2. Contoh Soal dan Pembahasan
Tentukan solusi umum dan solusi khusus persamaan diferensial dibawah ini!
1) 3x2 + (2y - 1) dy = 0, dimana y=2
2) xy3 dx + (2y + 1) x2 dy = 0, dimana y=10
Pembahasan:
1) 3x2 + (2y - 1) dy = 0, dimana y=2
3x2 + (2y − 1) dy = 0
x3 + y2 + y = C  Solusi Umum
x3 + (2)2 + 2 = C
x3 = -6  Solusi Khusus
2) xy3 dx + (2y + 1) x2 dy = 0, dimana y=10
xy3 dx + (2y + 1) x2 dy = 0
: y3 x2
𝑥 (2y + 1)
dx + dy = 0
𝑥2 𝑦3
𝑥 (2y + 1)
dx + dy = 0
𝑥2 𝑦3
𝐿𝑛 𝑥 + 2y + 1 𝐿𝑛 𝑦 3 = 𝐶  Solusi Umum
𝐿𝑛 𝑥 + 21 𝐿𝑛 1000 = 𝐶
𝐿𝑛 𝑥 = −145  Solusi Khusus
Page | 26

31. Tentukan orde dan carilah persamaan diferensial dari:
𝑑2 𝑥
1) y = y2 + 1
𝑑𝑦 2
𝑑𝑥 2
2) y = x2 + 1
𝑑𝑦
𝑑2 𝑡 𝑑𝑠
3) s +st =s
𝑑𝑠 2 𝑑𝑡
4) 𝑦" + 3𝑦 − 𝑥𝑦 = 0
5) 𝑥𝑦 ′ + 3𝑦 𝑠𝑖𝑛𝑥 + 2 = 0
Manakah diantara persamaan diferensial berikut yang merupakan persamaan diferensial
variable terpisah?
6) (x2 – y2) 𝑦 ′ + xy = 0
7) (x2 y2 – y2) 𝑦 ′ + x = 0
8) (x sin y – x2) 𝑦 ′ + cos x = 0
9) (x sin y – xy) 𝑦 ′ + (x2 + 1) y = 0
10) xy 𝑦 ′ + x2 + 1= 0
Tentukan solusi persamaan diferensial variable terpish dengan mereduksinya!
11) (x2 – 1) 𝑦 ′ + y2 + 1 = 0
12) (1 + 2y) 𝑑𝑥 + (x – 4) dy = 0
13) xy dx + (1 + x2) dy = 0
14) (xy + x) dx + (xy – y) dy = 0
𝑑𝑦 4𝑦
15) =
𝑑𝑥 𝑥𝑦 −3𝑥
Page | 27

32. Buktikan bahwa persamaan di bawah ini adalah persamaan diferensial homogeny kemudian,
carilah solusi umumnya!
16) 2xy dy = (x2 – y2) dx
𝑦 𝑦
17) x sin 𝑥 (y dx + x dy) + y cos 𝑥 (x dy – y dx) = 0
18) (x2 – 2y2) dy – 2xy dx = 0
𝑑𝑦 𝑥+𝑦
19) =
𝑑𝑥 𝑥
𝑑𝑦 4𝑦 −3𝑥
20) =
𝑑𝑥 2𝑥−𝑦
Tentukan solusi umum dari persamaan diferensial tak homogeny dibawah ini!
𝑑𝑦 6𝑥−2𝑦−7
21) = 2𝑥+3𝑦−6
𝑑𝑥
𝑑𝑦 1−2𝑦−4𝑥
22) =
𝑑𝑥 1+𝑦+2𝑥
23) (2x – 3y +5) dx + (24y – 8x – 40) dy = 0
24) (x – 5y +2) dx + (2x – 10x – 4) dy = 0
25) (2x – 5y +2) dx + (10y – 4x – 4) dy = 0
Tunjukkan bahwa PD berikut eksak dan tentukan selesaian umumnya!
26) (x+2y)dx + (y2+2x)dy = 0
27) 2y(x-y)dx + x(x-4y)dy = 0
28) (xsiny-y2)dy – cosy dx = 0
29) (3+y+2y2sin2x)dx – (ysin2x-2xy-x)dy = 0
30) xcos(xy)dy + (2x+ycos(xy))dx = 0
Tunjukkan bahwa fungsi yang diberikan adalah suatu faktor integrasi dan selesaikan
PD nya:
31) 2ydx+xdy = 0, x
32) sinydx+cosydy=0, 1/x2
33) y2dx+(1+xy)dy=0, exy
34) 2dx-ey-xdy = 0
35) (y+1)dx-(x+1)dy = 0
Page | 28

33. Selesaikan PD linier orde satu!
36) y’+(2x-1)y = xy2+(x-1)
37) y’+(2x4-1/x))y = x3 y2+x5
38) y’-2y/x = -y2/x+x2
39) y’+(2-1/x)y = y2-2/x
40) y’+2y+y2=0.
Tentukan Solusi Umum dari PD Bernoulli!
41) y’ + y = xy3
42) y’ = y (1 + xy)
𝑥
43) y - 2 y’ = 𝑦
44) 2xyy’ + y2 = x
45) Y’ – y = xy6
Tentukan Solusi khusus dari persamaan diferensial dibawah ini!
46) y'(t) = 3y + 5 , y(0) =1
47) y'(t) = ty +1 , y(0) = 0
48) y'= z, z'= -y , y(0) =1, z(0) = 0
1
49) y'(t) = − 1+ , y(0) =1
𝑦2
50) y” + 5y’ + 6y = 0, y(0) = 1
Page | 29

34. Lampiran

35. Basic Forms
(1)
(2)
(3)
(4)
Integrals of Rational Functions
(5)
(6)
(7)
(8)

36. (9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
Integrals with Roots
(17)

37. (18)
(19)
(20)
(21)
(22)
(23)
(24)
(25)
(26)

38. (27)
(28
)
(29)
(30)
(31)
(32)
(33)
(34)
(35)

39. (36)
(37
)
(38)
(39)
(40)
(41)
Integrals with Logarithms
(42)
(43)

40. (44)
(45)
(46)
(47)
(48)
(49)
(50)
(51
)
(52)

41. (53)
(54)
(55)
(56)
(57)
Integrals with Exponentials
(58)
(59)
erf where erf
(60)
(61)

42. (62)
(63)
(64)
(65)
d
(66)
where d
(67)
erf
(68)
erf
(69)
(70)
erf

43. Integrals with Trigonometric Functions
(71)
(72)
(73)
(74)
(75)
(76)
(77)
(78)

44. (79)
(80)
(81)
(82)
(83)
(84)
(85)
(86)
(87)

45. (88)
(89)
(90)
(91)
(92)
(93)
(94)
(95)
(96)

46. (97)
(98)
(99)
(100)
(101)
Products of Trigonometric Functions and Monomials
(102)
(103)
(104)
(105)

47. (106)
(107)
(108)
(109)
(110)
(111)
(112)
(113)
(114)

48. (115)
(116)
Products of Trigonometric Functions and Exponentials
(117)
(118)
(119)
(120)
(121)
(122)
Integrals of Hyperbolic Functions

49. (123)
(124)
(125)
(126)
(127)
(128)
(129)
(130)

50. (131)
(132)
(133)
(134)

51. SM. Nababan.2005.Persamaan Diferensial Biasa (Edisi Satu). Jakarta:Universitas Terbuka
Finizio and Ladas. 1988.Persamaan Diferensial Biasa dengan Penerapan Modern (Edisi
Kedua).Jakarta:Erlangga
Schaum’s.2007.Persamaan Diferensial (Edisi Ketiga).Jakarta: Erlangga
Varberg, Purcell, Rigdom.2003.Kalkulus Jilid 1. Jakarta: Erlangga
Sitanggang, Curmentyna.2003.Kamus Matematuka (Cetakan ketiga).Jakarta:Balai Pustaka
Soal Ujian Tenga Semester (UTS).2012.Persamaan Diferensial 1.Jakarta.Universitas
Indraprasta PGRI
http://uuniquee.files.wordpress.com/2010/09/persamaan_differensial_-_dr-_st-
_budi_waluya.pdf
http://file.upi.edu/Direktori/FPMIPA/JUR._PEND._MATEMATIKA/195804011985031-
ASEP_SYARIF_HIDAYAT/PERSAMAAN_DIFERENSIAL_I.pdf
http://math.ipb.ac.id/~files/tpb/9PersamaanDiferensialPrint_Mhs.pdf
http://alifis.files.wordpress.com/2009/09/bab-v-masalah-nilai-awal-persamaan-diferensial.pdf
http://dora.student.fkip.uns.ac.id/uncategorized/tutorial-maple-persamaan-differensial-
differential-equations/
http://staff.ui.ac.id/internal/131611668/material/mod-02.pdf
- D -