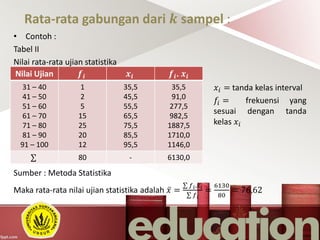
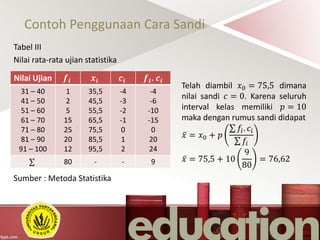
Dokumen tersebut membahas tentang ukuran gejala pusat dan ukuran letak dalam statistika. Ukuran gejala pusat mencakup rata-rata hitung, rata-rata ukur, rata-rata harmonik, dan modus, sedangkan ukuran letak mencakup median, kuartil, desil, dan persentil."

1. Statistika Dasar
Pertemuan ke-4
http://slideshare.net/QuKumeng

2. Ukuran Gejala Pusat dan Ukuran Letak
• Untuk mendapatkan gambaran yang lebih jelas
mengenai sekumpulan data, baik mengenai sampel atau
populasi, selain dari data itu disajikan dalam table dan
diagram, masih diperlukan ukuran-ukuran yang
merupakan wakil kumpulan data tersebut.
• Dalam bab ini akan diuraikan mengenai ukuran gejala
pusat dan ukuran letak.
• Ukuran yang dihitung dari kumpulan data dalam sampel
dinamakan statistic. Apabila ukuran itu dihitung dari
kumpulan data dalam populasi atau dipakai untuk
menyatakan populasi dinamakan parameter.

3. Ukuran Gejala Pusat
Ukuran gejala pusat menggambarkan gejala
pemusatan data. Misalkan diberikan peubah
acak 𝑋, dan diambil 𝑛 buah sampel acak untuk
𝑋 yaitu 𝑋1, 𝑋2, … , 𝑋 𝑛 dengan nilainya :
𝑥1, 𝑥2, … , 𝑥 𝑛 . Ukuran gejala pusat itu
diantaranya adalah:
• Mean atau Rata-Rata Hitung
• Rata-Rata Ukur
• Rata-Rata Harmonik
• Modus

4. Mean atau Rata-Rata Hitung
• Rumus umum mean (rata-rata) sampel :
𝑥 =
𝑥1+𝑥2+⋯+𝑥 𝑛
𝑛
atau 𝑥 = 𝑖=1
𝑛
𝑥 𝑖
𝑛
atau 𝑥 =
𝑥 𝑖
𝑛
• Contoh : jika terdapat lima nilai ujian mahasiswa
yaitu 70, 69, 45, 80, dan 56. Maka dalam simbul
ditulis 𝑥1 = 70, 𝑥2 = 69, 𝑥3 = 45, 𝑥4 = 80, 𝑥 𝑛 = 56
Dalam hal ini 𝑛 = 5, yang menyatakan sebuah
sampel berukuran 5.
• Untuk kelima nilai ujian di atas, nilai rata-ratanya :
𝑥 =
70 + 69 + 45 + 80 + 56
5
= 64

5. Mean atau Rata-Rata Hitung
• Rumus mean (rata-rata) sampel untuk data berkelompok :
𝑥 =
𝑖=1
𝑛
𝑓𝑖. 𝑥𝑖
𝑖=1
𝑛
𝑓𝑖
• Contoh : Jika ada lima mahasiswa mendapat nilai 70, enam mendapat 69,
tiga mendapat 45, dan masing-masing seorang mendapat nilai 80 dan 56.
Untuk contoh diatas baik ditulis dengan menggunakan tabel penolong
sebagai berikut:
Dari tabel didapat :
𝑓𝑖 = 16, dan
𝑓𝑖. 𝑥𝑖 = 1035, sehingga
𝑥 =
𝑓𝑖. 𝑥𝑖
𝑓𝑖
=
1035
16
= 64,6
𝒙𝒊 𝒇𝒊 𝒇𝒊. 𝒙𝒊
70
69
45
80
56
5
6
3
1
1
350
414
135
80
56
16 1035

6. Mean atau Rata-Rata Hitung
• Contoh : Data berikut merupakan daftar barang yang
disimpan di gudang, diantaranya terdapat yang rusak.
Tabel I
Daftar Barang yang Disimpan di Gudang
Sumber : Metoda Statistika
Barang Disimpan Rusak %
A
B
C
D
100
200
160
80
96
92
80
60
96
46
50
75
540 328 -

7. Mean atau Rata-Rata Hitung
• Jika rata-rata mengenai persen barang yang rusak dihitung dengan
menggunakan rumus yang pertama, maka :
𝑥 =
96 + 46 + 50 + 75
4
= 66,75 %
• Tetapi barang yang rusak ada 328 dari 540. Ini berarti
328
540
× 100% = 60,07 %
Hasil ini didapat dengan menggunakan rumus yang ke-2 seperti dalam daftar
berikut :
𝑥𝑖 = persen yang rusak
𝑓𝑖 = banyaknya barang
𝑥 =
𝑓𝑖. 𝑥𝑖
𝑓𝑖
× 100% =
328
540
= 60,07 %
𝒙𝒊(%) 𝒇𝒊 𝒇𝒊. 𝒙𝒊
96
46
75
75
100
200
160
80
96
92
80
60
540 328

8. Rata-rata gabungan dari 𝒌 sampel :
Merupakan rata-rata dari beberapa sub sampel lalu dijadikan satu. Jika
terdapat 𝑘 buah sub sampel masing-masing dengan keadaan berikut :
• Sub sampel 1 : berukuran 𝑛1 dengan rata-rata 𝑥1
• Sub sampel 2 : berukuran 𝑛2 dengan rata-rata 𝑥2
…
• Sub sampel 𝑘 : berukuran 𝑛 𝑘 dengan rata-rata 𝑥 𝑘
Maka rata-rata gabungan dari 𝑘 buah sub sampel :
𝑥 =
𝑛𝑖. 𝑥𝑖
𝑛𝑖
Contoh : lihat buku pegangan halaman 70.
Untuk data yang telah disusun dalam daftar distribusi frekuensi, rata-ratanya
dihitung dengan rumus :
𝑥 =
𝑓𝑖. 𝑥𝑖
𝑓𝑖

9. Rata-rata gabungan dari 𝒌 sampel :
• Contoh :
Tabel II
Nilai rata-rata ujian statistika
𝑥𝑖 = tanda kelas interval
𝑓𝑖 = frekuensi yang
sesuai dengan tanda
kelas 𝑥𝑖
Sumber : Metoda Statistika
Maka rata-rata nilai ujian statistika adalah 𝑥 =
𝑓 𝑖. 𝑥 𝑖
𝑓 𝑖
=
6130
80
= 76,62
Nilai Ujian 𝒇𝒊 𝒙𝒊 𝒇𝒊. 𝒙𝒊
31 – 40
41 – 50
51 – 60
61 – 70
71 – 80
81 – 90
91 – 100
1
2
5
15
25
20
12
35,5
45,5
55,5
65,5
75,5
85,5
95,5
35,5
91,0
277,5
982,5
1887,5
1710,0
1146,0
80 - 6130,0

10. Mean atau Rata-Rata Hitung dengan cara sandi
atau cara singkat
Rumus Cara Sandi :
𝑥 = 𝑥0 + 𝑝
𝑓𝑖. 𝑐𝑖
𝑓𝑖
𝑓𝑖 : frekuensi untuk nilai untuk 𝑥𝑖 yang bersesuaian.
𝑥0: tanda kelas dengan nilai sandi 𝑐𝑖 = 0.
𝑝 : Panjang interval kelas yang sama besarnya
Tanda kelas yang lebih besar dari 𝑥0 berturut-turut mempunyai
harga +1, +2, … dan sebaliknya −1, −2, …
 Cara sandi di atas hanya berlaku jika panjang kelas interval
semuanya sama.

11. Contoh Penggunaan Cara Sandi
Tabel III
Nilai rata-rata ujian statistika
Telah diambil 𝑥0 = 75,5 dimana
nilai sandi 𝑐 = 0. Karena seluruh
interval kelas memiliki 𝑝 = 10
maka dengan rumus sandi didapat
𝑥 = 𝑥0 + 𝑝
𝑓𝑖. 𝑐𝑖
𝑓𝑖
𝑥 = 75,5 + 10
9
80
= 76,62
Sumber : Metoda Statistika
Nilai Ujian 𝒇𝒊 𝒙𝒊 𝒄𝒊 𝒇𝒊. 𝒄𝒊
31 – 40
41 – 50
51 – 60
61 – 70
71 – 80
81 – 90
91 – 100
1
2
5
15
25
20
12
35,5
45,5
55,5
65,5
75,5
85,5
95,5
-4
-3
-2
-1
0
1
2
-4
-6
-10
-15
0
20
24
80 - - 9

12. Rata-Rata Ukur
• Digunakan bila perbandingan tiap dua data berurutan tetap atau
hampir tetap, rata-rata ukur lebih baik digunakan daripada rata-
rata hitung.
• Rumus umum rata-rata ukur : 𝑈 = 𝑛
𝑥1. 𝑥2. 𝑥3 … 𝑥 𝑛
• Contoh : Rata-rata ukur dari 2,4, dan 8 adalah :
𝑈 =
3
2 × 4 × 8 = 4
• Untuk data yang telah disusun dalam daftar distribusi frekuensi
rata-rata ukurannya dihitung dengan rumus :
log 𝑈 =
𝑓𝑖 log 𝑥𝑖
𝑓𝑖

13. Contoh Rata-Rata Ukur Distribusi Frekuensi
Tabel IV
Nilai rata-rata ujian statistika
Maka nilai rata-rata ukurnya :
log 𝑈 =
𝑓𝑖 log 𝑥𝑖
𝑓𝑖
log 𝑈 =
150,1782
80
= 1,8772
𝑈 = 75,37
Sumber : Metoda Statistika
Nilai Ujian 𝒇𝒊 𝒙𝒊 𝒍𝒐𝒈 𝒙𝒊 𝒇𝒊 𝐥𝐨𝐠 𝒙𝒊
31 – 40
41 – 50
51 – 60
61 – 70
71 – 80
81 – 90
91 – 100
1
2
5
15
25
20
12
35,5
45,5
55,5
65,5
75,5
85,5
95,5
1,5502
1,6580
1,7443
1,8162
1,8779
1,9320
1,9800
1,5502
3,3160
8,7215
27,2430
46,9475
38,6400
23,7600
80 - - 150,1782

14. Rata-Rata Harmonik
• Rumus umum rata-rata harmonik : H =
𝑛
1
𝑥 𝑖
=
𝑛
1
𝑥1
+
1
𝑥2
+⋯+
1
𝑥 𝑛
• Contoh : rata-rata harmonic untuk kumpulan data : 3,5,6,6,7,10, 12 dengan 𝑛
= 7 adalah :
𝐻 =
7
1
3
+
1
5
+
1
6
+
1
6
+
1
7
+
1
10
+
1
12
= 5,87
• Untuk data yang telah disusun dalam daftar distribusi frekuensi rata-rata
harmoniknya dihitung dengan rumus :
𝐻 =
𝑓𝑖
𝑓𝑖
𝑥𝑖

15. Contoh Rata-Rata Harmonik Distribusi Frekuensi
Tabel V
Nilai rata-rata ujian statistika
Maka nilai rata-rata harmonikya :
𝐻 =
𝑓𝑖
𝑓𝑖
𝑥𝑖
𝐻 =
80
1,0819
= 73,94
Sumber : Metoda Statistika
Nilai Ujian 𝒇𝒊 𝒙𝒊 𝒇𝒊/𝒙𝒊
31 – 40
41 – 50
51 – 60
61 – 70
71 – 80
81 – 90
91 – 100
1
2
5
15
25
20
12
35,5
45,5
55,5
65,5
75,5
85,5
95,5
0,0282
0,0440
0,0901
0,2290
0,3311
0,2339
0,1256
80 - 1,0819
𝑯 ≤ 𝑼 ≤ 𝒙

16. Modus
• Untuk menyatakan fenomena yang paling banyak terjadi atau paling
banyak terdapat digunakan ukuran modus disingkat Mo. Ukuran ini tanpa
disadari sering dipakai untuk menentukan rata-rata data kualitatif.
• Rumus modus untuk data terkelompok (data dalam distribusi frekuensi):
𝑀𝑜 = 𝑏 + 𝑝
𝑏1
𝑏1 + 𝑏2
𝑏 = batas bawah kelas modal, ialah kelas interval dengan frekuensi
terbanyak,
𝑝 = panjang kelas modal,
𝑏1 = frekuensi kelas modal dikurangi frekuensi kelas interval dengan tanda
kelas yang lebih kecil sebelum tanda kelas modal,
𝑏2 = frekuensi kelas modal dikurangi frekuensi kelas interval dengan tanda
kelas yang lebih besar sesudah tanda kelas modal.

17. Contoh Modus untuk Distribusi Frekuensi
Tabel VI
Nilai rata-rata ujian statistika
Maka nilai modusnya adalah:
𝑀𝑜 = 𝑏 + 𝑝
𝑏1
𝑏1 + 𝑏2
𝑀𝑜 = 70,5 + 10
10
10 + 5
𝑀𝑜 =77,17
Sumber : Metoda Statistika
Nilai Ujian 𝒇𝒊
31 – 40
41 – 50
51 – 60
61 – 70
71 – 80
81 – 90
91 – 100
1
2
5
15
25
20
12
80

18. Ukuran Letak
• Median
• Kuartil
• Desil
• Persentil

19. Median
• Median menentukan letak data setelah data itu disusun menurut
urutan nilainya. Jika ukuran data ganjil, maka median (Me)
merupakan data paling tengah setelah data diurutkan menurut
nilainya, tetapi jika ukuran data genap, maka median adalah
rata-rata dua data tengah setelah diurutkan.
• Contoh : sampel dengan data : 4,12,5,7,8,10,10,15. Setelah
disusun menurut nilainya menjadi : 4,5,7,8,10,10,12,15. Data
tengahnya bernilai 𝑀𝑒 =
1
2
8 + 10 = 9.
• Untuk data yang telah disusun dalam daftar distribusi frekuensi
mediannya dihitung dengan rumus :
𝑀𝑒 = 𝑏 + 𝑝
1
2
𝑛 − 𝐹
𝑓

20. Median
Untuk data yang telah disusun dalam daftar distribusi frekuensi
mediannya dihitung dengan rumus :
𝑀𝑒 = 𝑏 + 𝑝
1
2
𝑛 − 𝐹
𝑓
𝑏 = batas bawah kelas median, ialah kelas dimana median akan
terletak
𝑝 = panjang kelas median
𝑛 = banyak data
𝐹 = Jumlah semua frekuensi dengan tanda kelas lebih kecil dari
tanda kelas median
𝑓 = Frekuensi kelas median

21. Contoh Median untuk Distribusi Frekuensi
Tabel VII
Nilai rata-rata ujian statistika
Maka nilai modusnya adalah:
𝑀𝑒 = 𝑏 + 𝑝
1
2
𝑛 − 𝐹
𝑓
𝑀𝑒 = 70,5 + 10
1
2
(80) − 23
25
𝑀𝑒 =77,3
Sumber : Metoda Statistika
Nilai Ujian 𝒇𝒊
31 – 40
41 – 50
51 – 60
61 – 70
71 – 80
81 – 90
91 – 100
1
2
5
15
25
20
12
80

22. Hubungan Empiris Mean, Modus dan Median :
• Dari data yang telah kita buat, terlihat bahwa harga
statistika tersebut berlainan. Ketiga nilai yakni : rata-
rata, median, dan modus akan sama bila kurva
halusnya simetrik. Untuk fenomena dengan kurva
halus positif atau negative, hubungan empiriknya :
𝑀𝑒𝑎𝑛 − 𝑀𝑜 = 3 𝑀𝑒𝑎𝑛 − 𝑀𝑒
Dalam grafik, kedudukan ketiga nilai tersebut :

23. Kuartil
Jika sekumpulan data dibagi menjadi empat bagian yang sama
banyaknya, sesudah disusun menurut urutan nilainya, maka
bilangan pembaginya disebut kuartil. Ada tiga buah kuartil,
yaitu kuartil pertama 𝐾1 , kuartil kedua 𝐾2 , dan kuartil
ketiga 𝐾3 . Cara menentukan nilai kuartil :
• Susun data menurut urutan nilai
• Tentukan letak kuartil
• Tentukan nilai kuartil
Letak kuartil ke 𝑖, diberi lambang 𝐾𝑖, ditentukan oleh rumus :
𝐿𝑒𝑡𝑎𝑘 𝐾𝑖 = 𝑑𝑎𝑡𝑎 𝑘𝑒
𝑖(𝑛+1)
4
, dengan 𝑖 = 1,2,3

24. Contoh kuartil
• Misalkan terdapat data : 75,82,66,57,64,56,92,94,86,52,60,70.
• Susun menjadi : 52,56,57,60,64,66,70,75,82,86,92,94.
• Letak 𝐾1 = 𝑑𝑎𝑡𝑎 𝑘𝑒
1(12+1)
4
= 3
1
4
, yaitu antara data ke-3 dan data ke-4
seperempat jauh dari data ke-3.
• Nilai 𝐾1 = data ke-3 +
1
4
(data ke-4 – data ke-3)
𝐾1 = 57 +
1
4
60 − 57 = 57
3
4
• Letak 𝐾3 = 𝑑𝑎𝑡𝑎 𝑘𝑒
3(12+1)
4
= 9
3
4
, yaitu antara data ke-9 dan data ke-10 tiga
perempat jauh dari data ke-9.
• Nilai 𝐾3 = data ke-9 +
3
4
(data ke-10 – data ke-9)
𝐾3 = 82 +
3
4
86 − 82 = 85

25. Kuartil
Untuk data yang telah disusun dalam daftar distribusi frekuensi Kuartilnya
dihitung dengan rumus :
Nilai 𝐾𝑖 = 𝑏 + 𝑝
𝑖.𝑛
4
− 𝐹
𝑓
, dengan 𝑖 = 1,2,3
Dimana letak dari 𝐾𝑖 =
𝑖.𝑛
4
𝑏 = batas bawah kelas 𝐾𝑖, ialah kelas interval dimana 𝐾𝑖 akan terletak
𝑝 = panjang kelas 𝐾𝑖
𝑛 = banyak data
𝐹 = Jumlah semua frekuensi dengan tanda kelas lebih kecil dari tanda
kelas 𝐾𝑖
𝑓 = Frekuensi kelas 𝐾𝑖

26. Contoh Median untuk Distribusi Frekuensi
Tabel VIII
Nilai rata-rata ujian statistika
Tertukan nilai kuartil :
a. 𝐾1
b. 𝐾2
c. 𝐾3
Sumber : Metoda Statistika
Nilai Ujian 𝒇𝒊
31 – 40
41 – 50
51 – 60
61 – 70
71 – 80
81 – 90
91 – 100
1
2
5
15
25
20
12
80

27. Terimakasih
• Tugas :
Pelajari Kuartil, Desil, dan Persentil untuk data tunggal
dan data yang telah disusun dalam daftar distribusi
frekuensi.