This document provides an overview of mathematical logic and set theory concepts. It discusses topics such as mathematical logic and its subfields, basic set theory concepts like membership and subsets, set operations like union and intersection, and logical concepts like negation, conjunction, and syllogisms. It also explains logical form and provides examples of open and closed sentences as well as categorical and compound sentences.

1. English For Mathematics
Eleventh Lecture
http://www.slideshare.net/QuKumeng
https://www.mathsisfun.com/index.htm

2. Mathematical logic
• Mathematical logic is a subfield of mathematics exploring the
applications of formal logic to mathematics. It bears close connections
to metamathematics, the foundations of mathematics, and theoretical
computer science. The unifying themes in mathematical logic include
the study of the expressive power of formal systems and the deductive
power of formal proof systems.
• Mathematical logic is often divided into the fields of :
1. set theory,
2. model theory,
3. recursion theory, and
4. proof theory.
• These areas share basic results on logic, particularly first-order logic,
and definability. In computer science (particularly in the ACM
Classification) mathematical logic encompasses additional topics not
detailed in this article; see Logic in computer science for those.

3. Set theory
• Set theory is the branch of mathematical
logic that studies sets, which informally are
collections of objects. Although any type of
object can be collected into a set, set theory
is applied most often to objects that are
relevant to mathematics. The language of
set theory can be used in the definitions of
nearly all mathematical objects.

4. Basic concepts and notation Set Theory
• Set theory begins with a fundamental binary relation between
an object o and a set A. If o is a member (or element) of A, write
o ∈ A. Since sets are objects, the membership relation can relate
sets as well.
• A derived binary relation between two sets is the subset
relation, also called set inclusion. If all the members of set A are
also members of set B, then A is a subset of B, denoted A ⊆ B.
For example, {1,2} is a subset of {1,2,3} , and so is {2} but {1,4} is
not. From this definition, it is clear that a set is a subset of itself;
for cases where one wishes to rule this out, the term proper
subset is defined. A is called a proper subset of B if and only if A
is a subset of B, but B is not a subset of A. Note also that 1 and 2
and 3 are members (elements) of set {1,2,3} , but are not
subsets, and the subsets in turn are not as such members of the
set.

5. Basic concepts and notation Set Theory
• Just as arithmetic features binary operations on numbers, set theory features
binary operations on sets. The:
• Union of the sets A and B, denoted A ∪ B, is the set of all objects that are a
member of A, or B, or both. The union of {1, 2, 3} and {2, 3, 4} is the set {1, 2,
3, 4} .
• Intersection of the sets A and B, denoted A ∩ B, is the set of all objects that
are members of both A and B. The intersection of {1, 2, 3} and {2, 3, 4} is the
set {2, 3} .
• Set difference of U and A, denoted U A, is the set of all members of U that
are not members of A. The set difference {1,2,3} {2,3,4} is {1} , while,
conversely, the set difference {2,3,4} {1,2,3} is {4} . When A is a subset of U,
the set difference U A is also called the complement of A in U. In this case, if
the choice of U is clear from the context, the notation Ac is sometimes used
instead of U A, particularly if U is a universal set as in the study of Venn
diagrams.
• Symmetric difference of sets A and B, denoted A △ B or A ⊖ B, is the set of
all objects that are a

6. Basic concepts and notation Set Theory
• Just as arithmetic features binary operations on numbers, set theory features
binary operations on sets. The:
• Symmetric difference of sets A and B, denoted A △ B or A ⊖ B, is the set of
all objects that are a member of exactly one of A and B (elements which are
in one of the sets, but not in both). For instance, for the sets {1,2,3} and
{2,3,4} , the symmetric difference set is {1,4} . It is the set difference of the
union and the intersection, (A ∪ B) (A ∩ B) or (A B) ∪ (B A).
• Cartesian product of A and B, denoted A × B, is the set whose members are
all possible ordered pairs (a,b) where a is a member of A and b is a member
of B. The cartesian product of {1, 2} and {red, white} is {(1, red), (1, white), (2,
red), (2, white)}.
• Power set of a set A is the set whose members are all possible subsets of A.
For example, the power set of {1, 2} is { {}, {1}, {2}, {1,2} } .
• Some basic sets of central importance are the empty set (the unique set
containing no elements), the set of natural numbers, and the set of real
numbers.

7. Types of Sentences
• A mathematical sentence is one in which a fact or complete idea
is expressed. Because a mathematical sentence states a fact,
many of them can be judged to be "true" or "false". Questions
and phrases are not mathematical sentences since they cannot
be judged to be true or false.
1. "An isosceles triangle has two congruent sides." is a true
mathematical sentence.
2. "10 + 4 = 15" is a false mathematical sentence.
3. "Did you get that one right?" is NOT a mathematical sentence -
it is a question.
4. "All triangles" is NOT a mathematical sentence - it is a phrase.

8. There are two types of mathematical sentences:
An open sentence is a sentence which contains a variable.
• "x + 2 = 8" is an open sentence -- the variable is "x."
• "It is my favorite color." is an open sentence-- the variable is "It."
• The truth value of theses sentences depends upon the value
replacing the variable.
A closed sentence, or statement, is a mathematical sentence which
can be judged to be true or false. A closed sentence, or statement,
has no variables.
• "Garfield is a cartoon character." is a true closed sentence, or
statement.
• "A pentagon has exactly 4 sides." is a false closed sentence, or
statement.

9. A compound sentence
A compound sentence is formed when two or more thoughts are
connected in one sentence. Words such as and, or, if...then and if
and only if allow for the formation of compound sentences, or
statements. Notice that more than one truth value is involved in
working with a compound sentence.
• "Today is a vacation day and I sleep late."
• "You can call me at 10 o'clock or you can call me at 2 o'clock."
• "If you are going to the beach, then you should take your
sunscreen."
• "A triangle is isosceles if and only if it has two congruent sides."

10. Negation
• In logic, negation, also called logical complement, is an operation that takes a
proposition p to another proposition "not p", written ¬p, which is interpreted
intuitively as being true when p is false and false when p is true. Negation is
thus a unary (single-argument) logical connective. It may be applied as an
operation on propositions, truth values, or semantic values more generally. In
classical logic, negation is normally identified with the truth function that
takes truth to falsity and vice versa. In intuitionistic logic, according to the
Brouwer–Heyting–Kolmogorov interpretation, the negation of a proposition p
is the proposition whose proofs are the refutations of p.
• Classical negation is an operation on one logical value, typically the value of a
proposition, that produces a value of true when its operand is false and a
value of false when its operand is true. So, if statement A is true, then ¬A
(pronounced "not A") would therefore be false; and conversely, if ¬A is true,
then A would be false.
• The truth table of ¬p is as follows: 𝒑 ∼ 𝒑
True False
False True

11. Logical conjunction
• In logic and mathematics, and is the truth-functional operator of logical
conjunction; the and of a set of operands is true if and only if all of its
operands are true. The logical connective that represents this operator is
typically written as ∧ or ⋅ .
• "A and B" is true only if A is true and B is true.
• Venn diagram of 𝐴 ∧ 𝐵
• Logical conjunction is an operation on two logical
values, typically the values of two propositions,
that produces a value of true if and only if both
of its operands are true.

12. Logical Form
• Logic is generally considered formal when it analyzes and represents the form of any
valid argument type. The form of an argument is displayed by representing its
sentences in the formal grammar and symbolism of a logical language to make its
content usable in formal inference. If one considers the notion of form too
philosophically loaded, one could say that formalizing simply means translating
English sentences into the language of logic.
• This is called showing the logical form of the argument. It is necessary because
indicative sentences of ordinary language show a considerable variety of form and
complexity that makes their use in inference impractical. It requires, first, ignoring
those grammatical features irrelevant to logic (such as gender and declension, if the
argument is in Latin), replacing conjunctions irrelevant to logic (such as "but") with
logical conjunctions like "and" and replacing ambiguous, or alternative logical
expressions ("any", "every", etc.) with expressions of a standard type (such as "all", or
the universal quantifier ∀).
• Second, certain parts of the sentence must be replaced with schematic letters. Thus,
for example, the expression "all As are Bs" shows the logical form common to the
sentences "all men are mortals", "all cats are carnivores", "all Greeks are
philosophers", and so on.

13. Syllogism
• A syllogism (Greek: συλλογισμός syllogismos, "conclusion, inference") is a
kind of logical argument that applies deductive reasoning to arrive at a
conclusion based on two or more propositions that are asserted or assumed
to be true
• In its earliest form, defined by Aristotle, from the combination of a general
statement (the major premise) and a specific statement (the minor premise),
a conclusion is deduced. For example, knowing that all men are mortal (major
premise) and that Socrates is a man (minor premise), we may validly
conclude that Socrates is mortal. Syllogistic arguments are usually
represented in a three-line form (without sentence-terminating periods)
Basic structure
A categorical syllogism consists of three parts:
a. Major premise
b. Minor premise
c. Conclusion

14. Syllogism
• Each part is a categorical proposition, and each categorical proposition contains two
categorical terms. In Aristotle, each of the premises is in the form "All A are B," "Some
A are B", "No A are B" or "Some A are not B", where "A" is one term and "B" is
another. "All A are B," and "No A are B" are termed universal propositions; "Some A
are B" and "Some A are not B" are termed particular propositions. More modern
logicians allow some variation. Each of the premises has one term in common with
the conclusion: in a major premise, this is the major term (i.e., the predicate of the
conclusion); in a minor premise, it is the minor term (the subject) of the conclusion.
For example:
1) Major premise: All men are mortal
2) Minor premise: Socrates is a man
3) Conclusion: Therefore, Socrates is mortal
There are infinitely many possible syllogisms, but only 256 logically distinct types and only
24 valid types (enumerated below). A syllogism takes the form:
1. Major premise: All M are P.
2. Minor premise: All S are M.
3. Conclusion: All S are P.
(Note: M – Middle, S – subject, P – predicate. See below for more detailed explanation.)

15. Relationships between the
four types of propositions in
the square of opposition
(Black areas are empty,
red areas are nonempty.)

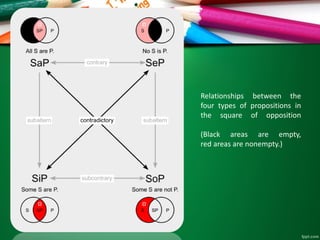
16. Syllogism
• The premises and conclusion of a syllogism can be any of four types, which
are labeled by letters[9] as follows. The meaning of the letters is given by the
table:
• In Analytics, Aristotle mostly uses the letters A, B and C (actually, the Greek
letters alpha, beta and gamma) as term place holders, rather than giving
concrete examples, an innovation at the time. It is traditional to use is rather
than are as the copula, hence All A is B rather than All As are Bs.

17. Syllogism
• On the other hand, in modern mathematical logic, however, statements
containing words "all", "some" and "no", can stated in terms of set theory. If
the set of all A's is labeled as s(A) and the set of all B's as s(B), then:
• By definition, the empty set is a subset of all sets. From this it follows that,
according to this mathematical convention, if there are no A's, then the
statements "All A is B" and "No A is B" are always true whereas the
statements "Some A is B" and "Some A is not B" are always false. This,
however, implies that AaB does not entail AiB, and some of the syllogisms
mentioned above are not valid when there are no A's.