Dokumen tersebut membahas tentang integral dan beberapa konsep dasarnya, meliputi:
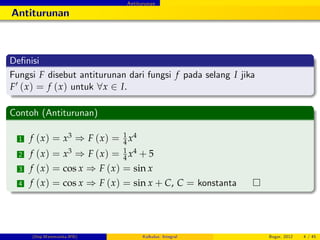
1. Definisi antiturunan dan beberapa contohnya
2. Penghitungan luas daerah di bawah kurva dengan pendekatan persegi panjang
3. Definisi integral tentu dan beberapa sifat integral





![Luas di Bawah Kurva
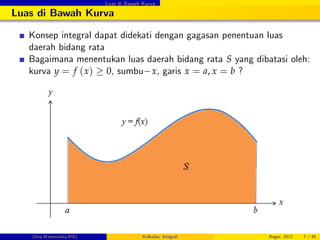
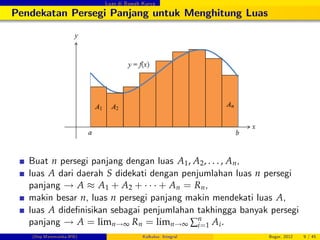
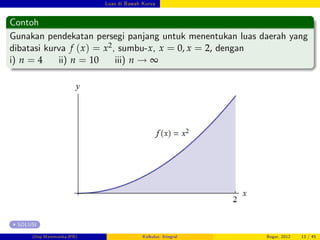
Penghitungan Luas dengan Pendekatan Persegi Panjang
Untuk menentukan luas daerah S yang dibatasi oleh: kurva kontinu
y = f (x) 0, sumbu x, garis x = a, x = b, lakukan:
Bagi selang [a, b] menjadi n
selang bagian [a = x0, x1] ,
[x1, x2] , . . . , [xn 1, xn = b]
dengan panjang yang sama,
yakni ∆x = b a
n , sehingga
berlaku xi = a + i∆x,
i = 1, 2, . . . , n.
Pada setiap selang bagian
[xi 1, xi] buat persegi panjang
dengan lebar ∆x dan panjang
f (xi), sehingga luas Ai =
f (xi) ∆x.
(Dep.Matematika-IPB) Kalkulus: Integral Bogor, 2012 10 / 45](https://image.slidesharecdn.com/5integralprintmhs-150611124640-lva1-app6891/85/integral-print-mhs-10-320.jpg)
![Luas di Bawah Kurva
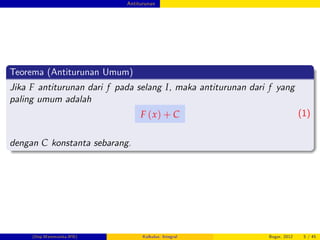
De…nisi
Luas A dari daerah S yang dibatasi oleh kurva kontinu y = f (x) 0,
sumbu x, garis x = a, x = b adalah
A = lim
n!∞
Rn = lim
n!∞
n
∑
i=1
f (xi) ∆x
= lim
n!∞
[f (x1) ∆x + f (x2) ∆x + + f (xn) ∆x]
(2)
dengan ∆x = (b a) /n, xi = a + i∆x, i = 1, 2, . . . , n.
Rn = ∑n
i=1 f (xi) ∆x pada (2) disebut Jumlah Riemann.
(Dep.Matematika-IPB) Kalkulus: Integral Bogor, 2012 11 / 45](https://image.slidesharecdn.com/5integralprintmhs-150611124640-lva1-app6891/85/integral-print-mhs-11-320.jpg)

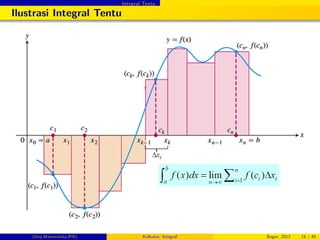
![Integral Tentu
Integral Tentu
Konsep Jumlah Riemann Rn = ∑n
i=1 f (xi) ∆x pada (2) dapat
diperluas untuk daerah yang ada di bawah sumbu-x (S2).
Jumlah Riemann pada S2 negatif karena f (xi) < 0.
Pada selang [a, b], lambang limit Jumlah Riemann dapat diganti
dengan lambang integral tentu,
limn!∞ ∑n
i=1 f (xi) ∆x =
R b
a
f (x) dx.
(Dep.Matematika-IPB) Kalkulus: Integral Bogor, 2012 14 / 45](https://image.slidesharecdn.com/5integralprintmhs-150611124640-lva1-app6891/85/integral-print-mhs-14-320.jpg)
![Integral Tentu
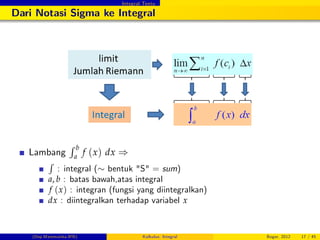
De…nisi (Integral Tentu)
Integral tentu fungsi f dari a ke b adalah
Z b
a
f (x) dx = lim
n!∞
n
∑
i=1
f (ci) ∆x (4)
dengan ci 2 [xi 1, xi] , ∆x = (b a) /n, [xi 1, xi] adalah selang bagian
ke-i dari [a, b] = [x0, xn] , i = 1, 2, . . . , n.
Titik sampel ci pada selang bagian [xi 1, xi] dapat berupa:
titik ujung kanan, ci = xi
titik ujung kiri, ci = xi 1
titik tengah, ci = (xi 1 + xi) /2
Syarat cukup agar f terintegralkan pada [a, b] adalah f kontinu pada
[a, b] .
(Dep.Matematika-IPB) Kalkulus: Integral Bogor, 2012 16 / 45](https://image.slidesharecdn.com/5integralprintmhs-150611124640-lva1-app6891/85/integral-print-mhs-16-320.jpg)


![Integral Tentu
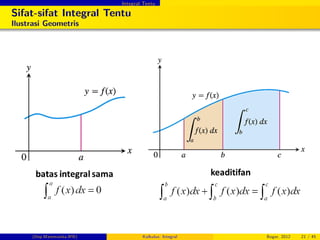
Sifat-sifat Integral Tentu
Sifat Umum
1
R a
b
f (x) dx =
R b
a
f (x) dx
2
R a
a
f (x) dx = 0
3
R b
a
c dx = c (b a)
4
R b
a
c f (x) dx = c
R b
a
f (x) dx
5
R b
a [f (x) g (x)] dx =
R b
a
f (x) dx
R b
a
g (x) dx
6
R b
a
f (x) dx +
R c
b
f (x) dx =
R c
a
f (x) dx
(Dep.Matematika-IPB) Kalkulus: Integral Bogor, 2012 22 / 45](https://image.slidesharecdn.com/5integralprintmhs-150611124640-lva1-app6891/85/integral-print-mhs-22-320.jpg)
![Integral Tentu
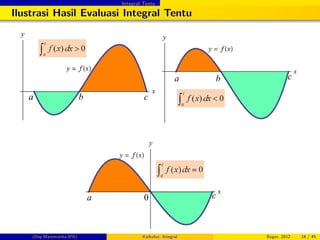
Sifat-sifat Integral Tentu
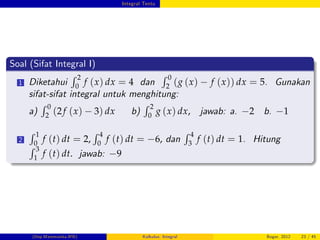
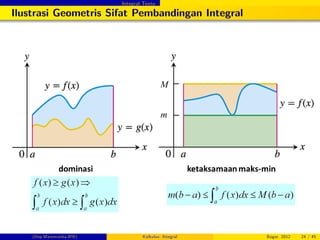
Sifat Pembandingan
1 Jika f (x) 0, x 2 [a, b], maka
R b
a
f (x) dx 0
2 Jika f (x) g (x) , x 2 [a, b], maka
R b
a
f (x) dx
R b
a
g (x) dx
3 Jika m f (x) M, x 2 [a, b], maka
m (b a)
R b
a
f (x) dx M (b a)
(Dep.Matematika-IPB) Kalkulus: Integral Bogor, 2012 25 / 45](https://image.slidesharecdn.com/5integralprintmhs-150611124640-lva1-app6891/85/integral-print-mhs-25-320.jpg)


![Teorema Dasar Kalkulus
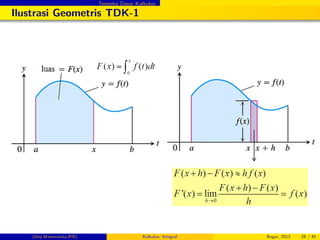
Teorema (Teorema Dasar Kalkulus 1)
Jika f kontinu pada [a, b], maka F (x) =
R x
a
f (t) dt kontinu pada [a, b],
terturunkan pada (a, b), dan turunannya adalah f (x) ;
F0 (x) = d
dx
R x
a
f (t) dt = f (x) (5)
(Dep.Matematika-IPB) Kalkulus: Integral Bogor, 2012 29 / 45](https://image.slidesharecdn.com/5integralprintmhs-150611124640-lva1-app6891/85/integral-print-mhs-29-320.jpg)
![Teorema Dasar Kalkulus
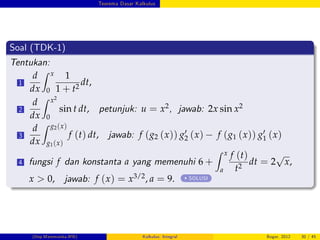
Teorema Dasar Kalkulus 2
Konsep
Dari TDK-1: G (x) =
R x
a
f (t) dt ) G0 (x) = f (x) (G antiturunan
f). Catat bahwa G (a) =
R a
a
f (t) dt = 0.
Misalkan F antiturunan lain dari f, maka F (x) = G (x) + C
F (b) F (a) = [G (b) + C] [G (a) + C]
= G (b) G (a) = G (b)
=
R b
a
f (t) dt =
R b
a
f (x) dx
Jadi
R b
a
f (x) dx = F (b) F (a)
dengan F merupakan antiturunan f atau F0 (x) = f (x) .
(Dep.Matematika-IPB) Kalkulus: Integral Bogor, 2012 31 / 45](https://image.slidesharecdn.com/5integralprintmhs-150611124640-lva1-app6891/85/integral-print-mhs-31-320.jpg)
![Teorema Dasar Kalkulus
Teorema (Teorema Dasar Kalkulus 2)
Jika f kontinu pada [a, b] dan F sebarang antiturunan f pada [a, b], maka
R b
a
f (x) dx = F (x) jb
a = F (b) F (a) (6)
TDK-2 memberi cara yang mudah dalam mengevaluasi integral tentu,
jauh lebih mudah dibandingkan menggunakan limit Jumlah Riemann.
Berdasarkan TDK-2, untuk mengevaluasi integral tentu f pada [a, b]:
tentukan antiturunan F dari f,
evaluasi F (b) F (a) .
(Dep.Matematika-IPB) Kalkulus: Integral Bogor, 2012 32 / 45](https://image.slidesharecdn.com/5integralprintmhs-150611124640-lva1-app6891/85/integral-print-mhs-32-320.jpg)







![Telaah Konsep
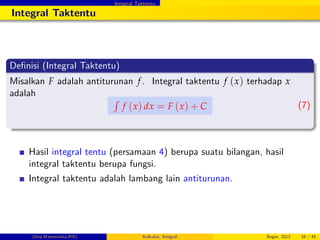
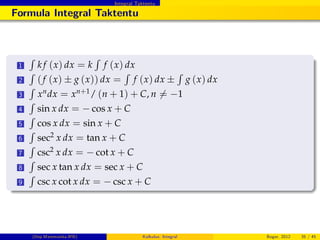
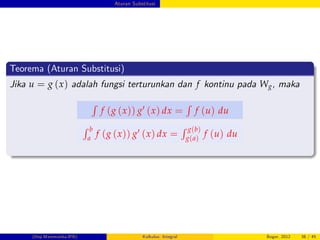
Telaah Konsep I
Kuis Benar-Salah
JAWABAN
1 Jika f dan g kontinu pada [a, b], maka
R b
a
f (x) g (x) dx =
R b
a
f (x) dx
R b
a
g (x) dx .
2 Jika f kontinu pada [a, b], maka
R b
a
x f (x) dx = x
R b
a
f (x) dx.
3 Jika
R b
a
f (x) dx = 0, maka f (x) = 0, x 2 [a, b] .
4 Jika
R b
a [f (x)]2
dx = 0, maka f (x) = 0, x 2 [a, b] .
5 Jika f kontinu pada [a, b] dan f (x) 0, maka
R b
a
p
f (x) dx =
qR b
a
f (x) dx
6 Jika f (x) g (x) pada [a, b], maka
R b
a jf (x)j dx
R b
a jg (x)j dx.
7 Jika f (x) g (x) pada [a, b], maka
R b
a
f (x) dx
R b
a
g (x) dx .
8 Jika a > x dan F (x) =
R x
a
f (t) dt, maka F0 (x) = f (x) .
(Dep.Matematika-IPB) Kalkulus: Integral Bogor, 2012 43 / 45](https://image.slidesharecdn.com/5integralprintmhs-150611124640-lva1-app6891/85/integral-print-mhs-43-320.jpg)
![Telaah Konsep
Telaah Konsep II
Kuis Benar-Salah
9 Jika F0 (x) = G0 (x) , x 2 [a, b], maka F (b) F (a) = G (b) G (a) .
10 Jika F (x) adalah antiturunan dari f (x), maka F (2x) adalah
antiturunan dari f (2x) .
11
Z 1
1
x3 2x7 +
sin x
1 + x2
dx = 0.
12
Z 11
11
ax2 + bx + c dx = 2
Z 11
0
ax2 + c dx.
13
Z 3
1
cos2 x dx =
Z 1
5
cos2 x dx +
Z 3
5
cos2 x dx.
14
d
dx
Z x2
1
1
1 + t2
dt =
1
1 + x4
.
15 lim
n!∞
n
∑
i=1
cos
2i
n
=
Z 2
0
cos x dx.
(Dep.Matematika-IPB) Kalkulus: Integral Bogor, 2012 44 / 45](https://image.slidesharecdn.com/5integralprintmhs-150611124640-lva1-app6891/85/integral-print-mhs-44-320.jpg)
