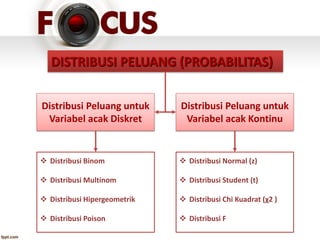
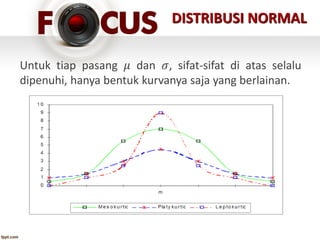
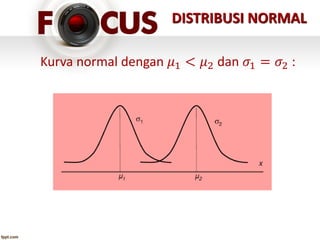
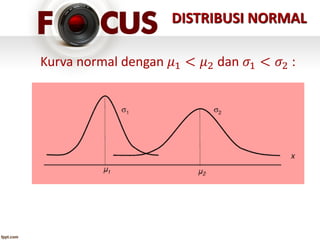
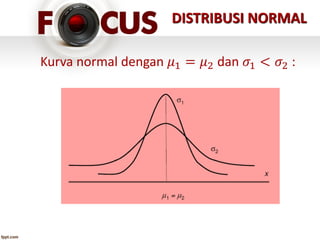
Dokumen tersebut membahas tentang distribusi peluang, baik untuk variabel acak diskrit maupun kontinu. Secara khusus, dibahas tentang distribusi normal yang merupakan distribusi peluang kontinu paling penting, dengan rata-rata (mean) dan variansi (standard deviation) sebagai parameternya. Distribusi normal memiliki bentuk kurva lonceng simetris di sekitar rata-ratanya.

1. STATISTIKA DASAR
Pertemuan ke-9
http://slideshare.net/QuKumeng

2. Tugas Kelompok :
• Buatlah kelompok yang terdiri dari 4 orang
• Masing-masing kelompok menentukan ketua
dari anggota tersebut
• Buatlah makalah lengkap mengenai :
a. Peluang beserta aturan-aturannya
b. Distribusi peluang diskrit beserta aturan-
aturannya
c. Contoh-contoh dari peluang dan distribusi
peluang diskrit
d. Carilah Tabel-Tabel distribusi peluang Kontinu

3. DISTRIBUSI PELUANG (PROBABILITAS)
• Bahasan pada distribusi probabilitas adalah
penyusunan distribusi frekuensi yang
berdasarkan teori peluang. Oleh karena itu,
disebut distribusi frekuensi teoritis atau
distribusi peluang atau distribsi probabilitas.
• Karena distribusi frekuensi probabilitas
disusun berdasarkan teori peluang maka
pengetahuan tentang distribusi teoritis
menjadi sangat penting untuk membuat
estimasi atau meramalkan variasi-variasi yang
mungkin dapat timbul pada suatu keadaan
yang tidak pasti.
• Distribusi peluang didefinisikan dengan suatu
fungsi peluang, dinotasikan dengan p(x) atau
f(x), yang menunjukkan peluang untuk setiap
nilai variabel acak.

4. VARIABEL ACAK DISKRIT
Suatu variabel disebut variabel acak apabila variabel tersebut
menghasilkan nilai yang selalu berbeda pada setiap peristiwa (trial)
dan perubahan tersebut tidak dapat diperkirakan.
Misalnya seorang petugas poliklinik disuatu rumahsakit dengan
cara apapun tidak dapat mengetahui secara pasti banyaknya
kunjungan pada esok hari. Maka jumlah kunjungan pada esok hari
disebut variabel acak. Namun, petugas tersebut dapat menentukan
probabilitas menggunakan catatan medik yang ada. Bila dia
mengetahui bahwa jumlah kunjungan per hari berkisar antara 40
dan 55 orang maka dia dapat menyusunnya menjadi distribusi
frekuensi dan membuat prakiraan atau probabilitas kunjungan.
Karena variasi jumlah kunjungan berkisar antara 40 dan 55 orang
yaitu bersifat variable (0, 1, 2, …) dan memiliki harga-harga absolut,
maka variabel acak tersebut disebut variabel acak diskrit.

5. Ditribusi Peluang Diskrit
Distribusi peluang diskrit, yaitu apabila variabel acak yang
digunakan adalah variabel acak diskrit. Syarat distribusi
peluang untuk variable acak X adalah:
𝑝(𝑥) ≥ 0, nilai peluang selalu lebih besar atau sama
dengan 0, dan
𝑃 𝑋 = 𝑥𝑖 =
𝑖=1
𝑛
𝑝 𝑥𝑖 = 1
Yaitu jumlah total peluang pada sebuah kejadian sama
dengan 1, dengan 𝑝(𝑥) disebut fungsi peluang untuk
variable acak 𝑋 pada harga 𝑋 = 𝑥.
Distribusi peluang diskrit dapat digambarkan dalam bentuk
tabel, grafik, maupun persamaan.

6. Sumber : Google
Jumlah kunjungan Frekuensi
40 1
41 2
42 3
43 5
44 6
45 7
46 9
47 10
48 11
49 12
50 9
51 8
52 6
53 5
54 4
55 2
Jumlah 100
Tabel 1.
jumlah kunjungan poliklinik 100 hari
Data tentang jumlah kunjungan
pada poliklinik dapat diubah
menjadi distribusi frekuensi.
Misalnya, jika petugas tersebut
mengambil sebanyak 100 hari
kerja maka akan diperoleh tabel
distribusi frekuensi sebagai
berikut.

7. Sumber : Google
Tabel 2.
Distribusi kunjungan poliklinik tiap hari
Dari frekuensi distribusi
tersebut dapat diketahui
probabilitas jumlah kunjungan
setiap hari dengan membagi
kunjungan setiap hari dengan
jumlah hari buka yang
digunakan, yaitu 100 hingga
dapat disusun distribusi jumlah
kunjungan dengan probabilitas
nya dan dari distribusi tersebut
dapat dibuat grafik untuk
memudahkan penilaian.
Jumlah kunjungan Probabilitas
40 0,01
41 0,02
42 0,03
43 0,05
44 0,06
45 0,07
46 0,09
47 0,10
48 0,11
49 0,12
50 0,09
51 0,08
52 0,06
53 0,05
54 0,04
55 0,02
Jumlah 1,00

8. Nilai Expektasi Variabel acak Diskrit
Nilai ekspektasi banyak digunakan dalam keadaan yang tidak
pasti atau data yang diperoleh tidak lengkap atau bahkan
mungkin tidak ada data sama sekali. Untuk menghitung
besarnya nilai ekspektasi dari variabel acak yang deskrit tidak
sulit karena nilai tersebut merupakan perkalian antara
variabel acak dengan probabilitasnya. Untuk sebuah variable
acak kita dapat menentukan ekspektasinya, yaitu :
𝐸 𝑋 = 𝑥𝑖. 𝑝(𝑥𝑖)
Dimana 𝐸 𝑋 = ekspektasi untuk variable acak 𝑋 dan
penjumlahan dilakukan untuk semua harga 𝑋 yang mungkin.

9. Variabel acak kontinu
Variabel acak yang tidak diskrit atau Bila variasi
sedemikian banyaknya hingga nilai dalam satu rentang
(range) tertentu dapat disisipkan nilai sedemikian
banyaknya hingga berhimpitan disebut variable acak
kontinu.
Beberapa diantaranya, misalnya untuk menyatakan
waktu dan hasil pengukuran. Variabel ini dapat
mempunyai setiap harga. Jadi, jika 𝑋 = variable acak
kontinu, maka harga 𝑋 = 𝑥 dibatasi oleh −∞ < 𝑥 < ∞.

10. Ditribusi Peluang Kontinu
Distribusi peluang kontinu, yaitu apabila variabel acak yang digunakan
adalah variabel kontinu. Jika 𝑋 sebuah variable kontinu, maka kita
memiliki fungsi densitas 𝑓 𝑥 , Syaratnya adalah:
1. 𝑓(𝑥) ≥ 0, nilai peluang selalu lebih besar atau sama dengan 0,
dan
2. −∞
∞
𝑓 𝑥 𝑑𝑥 = 1
3. Peluang dihitung untuk nilai dalam suatu interval tertentu
4. Peluang di suatu titik = 0
5. Peluang untuk random variabel kontinu (nilai-nilainya dalam suatu
interval), misalkan antara 𝑥1 dan 𝑥2 , didefinisikan sebagai luas
daerah di bawah kurva (grafik) fungsi peluang antara 𝑥1 dan 𝑥2 .
Distribusi peluang kontinu dapat digambarkan dalam bentuk tabel,
grafik, maupun persamaan.

11. Ditribusi Peluang Kontinu dan Expektasinya
Untuk menentukan peluang bahwa harga 𝑋 = 𝑥
antara a dan b, maka digunakan rumus :
𝑃 𝑎 < 𝑋 < 𝑏 =
𝑎
𝑏
𝑓 𝑥 𝑑𝑥
Untuk sebuah variable acak kita dapat menentukan
ekspektasinya, yaitu :
𝐸 𝑋 =
−∞
∞
𝑥. 𝑓(𝑥) 𝑑𝑥

12. DISTRIBUSI PELUANG (PROBABILITAS)
Distribusi Peluang untuk
Variabel acak Diskret
Distribusi Peluang untuk
Variabel acak Kontinu
 Distribusi Binom
 Distribusi Multinom
 Distribusi Hipergeometrik
 Distribusi Poison
 Distribusi Normal (z)
 Distribusi Student (t)
 Distribusi Chi Kuadrat (χ2 )
 Distribusi F

13. Distribusi normal adalah distribusi yang paling penting
diantara distribusi yang lain. Nama lainnya: distribusi
Gauss (Gaussian distribution). Kurva dari distribusi
normal mempunyai bentuk setangkup seperti lonceng :
Fungsi padat peluang (pdf) dari
peubah acak normal X dengan
rataan μ dan variansi 𝜎2 yang
memiliki distribusi normal
adalah:
𝑛 𝑥; 𝜇, 𝜎 =
1
𝜎 2𝜋
𝑒
−1/2
𝑥−𝜇
𝜎
2
, −∞ < 𝑥 < ∞
yang dalam hal ini π = 3.14159... dan e = 2.71828...
DISTRIBUSI NORMAL

14. • Rata-ratanya (mean) μ dan standard deviasinya = σ
• Grafiknya selalu ada di atas sumbu datar x
• Bentuknya simetrik terhadap 𝑥 = 𝜇
• Mode (maximum) terjadi di 𝑥 = 𝜇
• Titik belok tepat di 𝑥 = 𝜇 ± 𝜎
• Memiliki satu modus, jadi kurva unimodal, tercapai pada
𝑥 = 𝜇 sebesar
0,3989
𝜎
• Grafiknya mendekati sumbu datar x dimulai dari 𝑥 = 𝜇 +
3𝜎 ke kanan 𝑥 = 𝜇 − 3𝜎 ke kiri
• Luas daerah grafik selalu sama dengan satu unit persegi
Sifat-Sifat Distribusi Normal:
DISTRIBUSI NORMAL

15. Untuk tiap pasang 𝜇 dan 𝜎, sifat-sifat di atas selalu
dipenuhi, hanya bentuk kurvanya saja yang berlainan.
DISTRIBUSI NORMAL

16. Kurva normal dengan 𝜇1 < 𝜇2 dan 𝜎1 = 𝜎2 :
DISTRIBUSI NORMAL

17. Kurva normal dengan 𝜇1 < 𝜇2 dan 𝜎1 < 𝜎2 :
DISTRIBUSI NORMAL

18. Kurva normal dengan 𝜇1 = 𝜇2 dan 𝜎1 < 𝜎2 :
DISTRIBUSI NORMAL

19. DISTRIBUSI NORMAL STANDAR