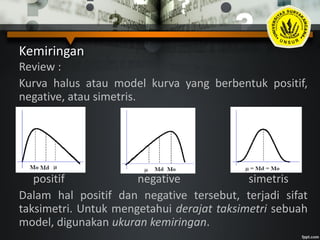
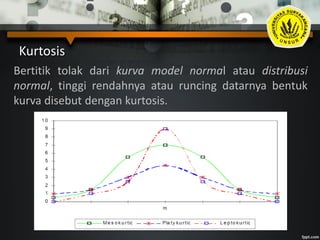
Momen dan kurtosis merupakan ukuran penting untuk menganalisis distribusi data. Momen digunakan untuk menghitung rata-rata, variansi, kemiringan, dan bentuk kurva secara umum, sedangkan kurtosis mengukur tingkat keruncingan atau kedataran suatu kurva distribusi relatif terhadap kurva normal. Koefisien kurtosis memungkinkan penetapan apakah suatu distribusi bersifat leptokurtik, platikurtik, atau mesokurtik

1. Statistika Dasar
Pertemuan ke-8
http://slideshare.net/QuKumeng

2. Momen untuk data tunggal
Misalkan diberikan variable 𝑥 dengan harga-harga :
𝑥1, 𝑥2, … , 𝑥 𝑛. Jika 𝐴 = sebuah bilangan tetap dan 𝑟 =
1,2, … , maka momen ke-r sekitar A, disingkat 𝑚′ 𝑟
didefinisikan oleh hubungan :
𝑚′ 𝑟 =
(𝑥𝑖 − 𝐴) 𝑟
𝑛
Untuk 𝐴 = 0 didapat momen ke-r sekitar nol atau disingkat
momen ke-r :
𝑀𝑜𝑚𝑒𝑛 𝑘𝑒 − 𝑟 =
𝑥𝑖
𝑟
𝑛
Dari rumus diatas, maka untuk 𝑟 = 1 didapat rata-rata 𝑥

3. Momen untuk data tunggal
untuk 𝑟 = 1 didapat rata-rata 𝑥. Jika 𝐴 = 𝑥, kita
peroleh momen ke-r sekitar rata-rata, biasa
disingkat dengan 𝑚 𝑟. Didapat :
𝑚 𝑟 =
(𝑥 𝑖− 𝑥) 𝑟
𝑛
Untuk 𝑟 = 2, rumus diatas memberikan varians
𝑠2
. Maka rata-rata dan varians sebenarnya
merupakan hal istimewa dari kelompok ukuran
lain yang disebut momen.
Untuk membedakanapakah momen itu untuk
sampel atau populasa, maka dipakai simbul :
• 𝑚 𝑟 dan 𝑚′ 𝑟 untuk momen sampel
• 𝜇 𝑟 dan 𝜇′ 𝑟 untuk momen populasi

4. Momen untuk data distribusi frekuensi
Bila data telah disusun dalam daftar distribusi frekuensi,
maka rumus-rumus diatas berturut-turut berbentuk :
𝑚′ 𝑟 =
𝑓𝑖(𝑥𝑖 − 𝐴) 𝑟
𝑛
𝑀𝑜𝑚𝑒𝑛 𝑘𝑒 − 𝑟 =
𝑓𝑖. 𝑥𝑖
𝑟
𝑛
𝑚 𝑟 =
𝑓𝑖(𝑥𝑖 − 𝑥) 𝑟
𝑛
Dengan 𝑛 = 𝑓𝑖, 𝑥𝑖 = tanda kelas interval, dan 𝑓𝑖 =
frekuensi yang sesuai dengan 𝑥𝑖.

5. Momen untuk data distribusi frekuensi
Dengan menggunakan cara sandi, maka :
𝑚′ 𝑟 = 𝑝 𝑟
𝑓𝑖. 𝑐𝑖
𝑟
𝑛
Dengan 𝑝 =panjang kelas dan 𝑐𝑖 = variable sandi.
Dari 𝑚′ 𝑟 harga 𝑚 𝑟 untuk beberapa harga r, dapat
ditentukan berdasarkan hubungan :
𝑚2 = 𝑚′2 − (𝑚′
1)2
𝑚3 = 𝑚′3 − 3𝑚′1 𝑚′2 + 2(𝑚′
1)3
𝑚4 = 𝑚′4 − 4𝑚′
1 𝑚′
3 + 6 𝑚′
1
2 𝑚′
2 − 3(𝑚′
1)4

6. Contoh Momen :
Carilah empat buah momen
sekitar rata-rata untuk data
dalam daftar distribusi
frekuensi disamping:
a. Dengan menggunakan cara
sandi.
b. Tentukan 𝑚1, 𝑚2, 𝑚3, 𝑚4
c. Tentukan rata-rata dan
varians nya.
Tabel IV
Nilai rata-rata ujian
statistika
Sumber : Metoda Statistika
Nilai Ujian 𝒇𝒊
31 – 40
41 – 50
51 – 60
61 – 70
71 – 80
81 – 90
91 – 100
1
2
5
15
25
20
12
80

7. Kemiringan
Review :
Kurva halus atau model kurva yang berbentuk positif,
negative, atau simetris.
positif negative simetris
Dalam hal positif dan negative tersebut, terjadi sifat
taksimetri. Untuk mengetahui derajat taksimetri sebuah
model, digunakan ukuran kemiringan.

8. Kemiringan
Ukuran kemiringan :
𝐾𝑒𝑚𝑖𝑟𝑖𝑛𝑔𝑎𝑛 =
𝑥 − 𝑀𝑜
𝑠
Rumus empiriknya :
𝐾𝑒𝑚𝑖𝑟𝑖𝑛𝑔𝑎𝑛 =
3( 𝑥 − 𝑀𝑒)
𝑠
• Kurva positif (+) terjadi bila kurva mempunyai ekor yang
memanjang ke kanan sehingga kemiringan (+).
• Kurva negative (-) terjadi bila kurva mempunyai ekor yang
memanjang ke kiri sehingga kemiringan (–) .
• Kurva simetri terjadi bila kurvamemiliki ekor yang sama
panjang antara kanan dan kiri sehingga kemiringan (0).

9. Contoh Kemiringan
a. Tentukan Kemiringan
dari Tabel disamping.
b. Kemudian tentukan
apakah tabel disamping
memiliki kurva positif,
negative, atau simetri.
c. Lihat Buku Halaman 55
Tabel IV
Nilai rata-rata ujian
statistikaa.
Sumber : Metoda Statistika
Nilai Ujian 𝒇𝒊
31 – 40
41 – 50
51 – 60
61 – 70
71 – 80
81 – 90
91 – 100
1
2
5
15
25
20
12
80

10. Kurtosis
Bertitik tolak dari kurva model normal atau distribusi
normal, tinggi rendahnya atau runcing datarnya bentuk
kurva disebut dengan kurtosis.

11. Kurtosis
Salah satu ukuran kurtosis ialah koefisien kurtosis yang
diberi simbul 𝑎4, dengan rumus :
𝑎4 =
𝑚4
𝑚2
2
Kriteria yang didapat dari rumus ini adalah :
• 𝑎4 = 3 memiliki distribusi normal
• 𝑎4 > 3 memiliki distribusi leptokurtic
• 𝑎4 < 3 memiliki distribusi platikurtik

12. Kurtosis
Untuk menyelidiki apakah distribusi tersebut normal atau
tidak, maka dipakai koefisien kurtosis persentil :
𝐾 =
1
2
(𝐾3 − 𝐾1)
𝑃90 − 𝑃10
Koefisien kurtosis kurva normal = 0,263.
Kurva yang runcing disebut leptokurtik , koefisien
keruncingannya lebih dari 0,263. Sedangkan kurva yang
datar disebut platikurtik, koefisien keruncingannya kurang
dari 0,263. Kurva yang bentuknya antara runcing dan
datar disebut mesokurtik.