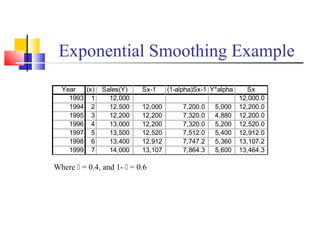
Time series analysis examines patterns in data over time. It relies on identifying trends, measuring past patterns to forecast the future, and decomposing time series into four main components: secular trends, cyclical movements, seasonal variations, and irregular variations. Secular trends represent long-term direction, while cyclical and seasonal variations have recurring patterns over different time scales. Various techniques can depict trends and identify variations, including freehand drawing, semi-averages, moving averages, least squares, and exponential smoothing.

1. Time Series and Trend Analysis

2. Time Series
 Time series examines a series of data over time
 In studying the series, patterns become evident
and these patterns are used to assist with future
decision making
 Time series relies on the following;
 Identification of the underlying trend line
 Measurement of past patterns and the assumption that
these patterns will be repeated in the future
 Forecast of future trends of data

3. Components of Time Series
 The four main components of time series are;
 Secular trend
 Cyclical movement
 Seasonal movement
 Irregular movement

4. 1. Secular Movement
 A secular trend identifies the underlying trend of the data
 It is the long term direction of the data, usually described by the
‘line of best fit’
 The secular trend is influenced by;
 Population
 Productivity improvement
 Technological changes
 Market changes
 The most common methods for depicting the secular trends are;
 Freehand drawing
 Semi-average
 Least-squares method
 Exponential smoothing

5. 1a Freehand Drawing
 Freehand drawing involves plotting the data on a
scatter diagram
 From the plots you should be able to get an idea of
the trend
y
x

6. 1b Semi-Averages
 The semi-average technique is as follows;
 Divide the data into two equal time ranges
 Average each of the two time ranges
 Draw a straight line through the two points

7. Semi-Averages Example
 Annual soft drink sales
Year 1991 1992 1993 1994 1995 1996 1997 1998 1999
$ ' millions 13 15 17 18 19 20 20 21 22
1991 13 1996 20
1992 15 1997 20
1993 17 1998 21
1994 18 1999 22
63 83
63/4 = 15.75 83/4 = 20.75
Annual Soft Drink Sales
0
5
10
15
20
25
1991/92 1992/93 1993/94 1994/95 1995/96 1996/97 1997/98 1998/99
Year
$'millions

8. Class Exercise 2
 Calculate the co-ordinates for the semi average trend line
 Graph the data and draw the trend line
 Estimate the value for year 12 using the line of best fit
Year 1 2 3 4 5 6 7 8 9 10 11
Data 10200 10800 11400 12200 13300 14700 15900 17200 18400 19500 20900

9. 1c Moving Average
 The technique for finding a moving average for a
particular observation is to find the average of the
m observations before the observation, the
observation itself and the m observations after the
observation
 Thus a total of (2m + 1) observations must be
averaged each time a moving average is calculated

10. Moving Average Example
 Annual soft drink sales
Year
$ '
millions
3yr
Moving
Total
3yr
Moving
Ave.
1991 13
1992 15 45 15.00
1993 17 50 16.67
1994 18 54 18.00
1995 19 57 19.00
1996 20 59 19.67
1997 20 61 20.33
1998 21 63 21.00
1999 22

11. Class Exercise 1
 Calculate the following;
 The trend line for a three year moving average
 The trend line for a five year moving average
Year 1 2 3 4 5 6 7 8 9
Data 324 296 310 305 295 347 348 364 370
Year Data 3yr MT 3yr MA 5yr MT 5yr MA
1
2
3
4
5
6
7
8
9

12. 1d Least-Squares Method
 This method uses the given series of data to
develop a trend line for predictive purposes
 The least-squares method establishes a trend line
from;
 Yt = a + bx where a =
b =
n
y∑
∑
∑
2
x
xy

13. Least-Squares Method Example
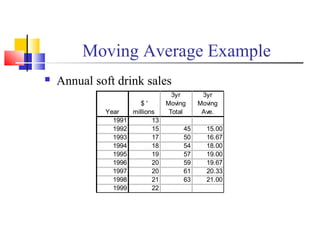
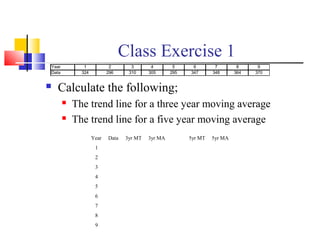
 Annual soft drink sales
 Find the expected sales for 2001
Year Y [x] x2
xy
1991 13 -4 16 -52
1992 15 -3 9 -45
1993 17 -2 4 -34
1994 18 -1 1 -18
1995 19 0 0 0
1996 20 1 1 20
1997 20 2 4 40
1998 21 3 9 63
1999 22 4 16 88
165 60 62
Y is the given data
X is the year value in relation to the middle year
03.1
60
62
2
=
=
=
∑
∑
b
b
x
xy
b
3.18
9
165
=
=
=
∑
a
a
n
y
a
Yt = 18.3 + 1.03x
2001 Yt = 18.3 + 1.03(6)
= 18.3 + 6.18
= 22.48
Expected sales for 2001 = $22,480,000

14. 1e Exponential Smoothing
 Exponential smoothing is a method of deriving a trend line where past
history of the variable in question is used to ‘flatten out’ short term
fluctuations
 A ‘smoothing constant’ ( - alpha) is included with a value between 0 and 1
 The value of  is nominated according to the emphasis one wishes to place
on the past
 The formula is;
 Sx = Y + (1 - ) Sx – 1
 Where Y = The observed value
  = The nominated smoothing constant
 Sx = The smoothed value of the given period
 Sx-1 = The smoothed value of the previous period
 x = The given period

15. Exponential Smoothing Example
Year (x) Sales(Y) Sx-1 (1-alpha)Sx-1 Y*alpha Sx
1993 1 12,000 12,000.0
1994 2 12,500 12,000 7,200.0 5,000 12,200.0
1995 3 12,200 12,200 7,320.0 4,880 12,200.0
1996 4 13,000 12,200 7,320.0 5,200 12,520.0
1997 5 13,500 12,520 7,512.0 5,400 12,912.0
1998 6 13,400 12,912 7,747.2 5,360 13,107.2
1999 7 14,000 13,107 7,864.3 5,600 13,464.3
Where  = 0.4, and 1-  = 0.6

16. Exponential Smoothing Using Excel
Step 1. Open Sample 1 workbook
Step 2. Open Exponential Smoothing worksheet
Step 3. Select Tools – Data Analysis – Exponential Smoothing –
Click OK

17. Exponential Smoothing Using Excel
Step 4. Enter Input Range – (C2:C10 in this example)
Step 7. Enter Damping Factor (1 – alpha)
Step 8. Click Labels (if you highlighted a label in your input range)
Step 9. Select output cell (D2 in this example)
Step 10. Click OK

18. Class Exercise 3
 The private consumption
expenditure on
entertainment in Future
World is shown in the
table across.
 Obtain the trend values for
this data using the Method
of Exponential Smoothing
where the smoothing
constant = 0.4
 Calculate expenditure for
2001/02 & trend value
Year Expenditure $'000
1990/91 2,020
1991/92 2,050
1992/93 2,030
1993/94 2,625
1994/95 2,970
1995/96 3,265
1996/97 3,575
1997/98 3,745
1998/99 3,970

19. 2. Cyclical Variation
 Cyclical variations have recurring patterns over a
longer and more erratic time scale
 There are a number of techniques for identifying
cyclical variation in a time series
 One method is the residual method

20. 3. Seasonal Variation
 The seasonal variation of a time series is a pattern
of change that recurs regularly over time
 Seasonal variations are usually due to the
differences between seasons and to festive
occasions
 Time series graphs may be prepared using an
adjustment for seasonal variations
 Such graphs are said to be seasonally adjusted

21. 4. Irregular Variation
 Irregular variation in a time series occurs over
varying (usually short) periods
 It follows no regular pattern and is by nature
unpredictable