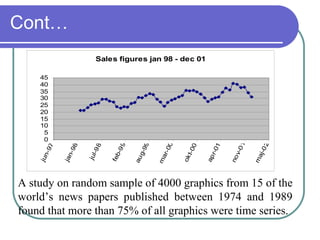
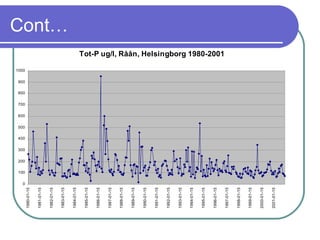
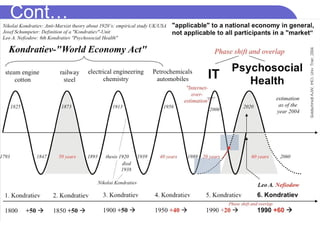
This document discusses time series analysis. It defines a time series as a collection of observations made sequentially over time. Examples include financial, scientific, demographic, and meteorological time series data. The document contrasts time series data with cross-sectional data. It also describes the components of a time series, including trends, seasonal variations, cyclical variations, and irregular/random variations. The purposes and uses of time series analysis are discussed, along with methods for decomposing and measuring trends in time series data.

1. Time Series Analysis

2. Time Series Analysis
A Time Series is a collection of observations made
sequentially in time.
According to Ya-lun Chou, “A Time Series may be
defined as a collection of readings belonging to
different time periods, of some economic variables
or composite of variables”
Examples: Financial time series, scientific time series,
Demographic time series, Meteorological time series

3. Time series data Vs. Cross Sectional data
Time series data Cross Sectional data
Time-series data is a set of observations
collected at usually equally spaced time
intervals.
Cross-sectional data are observations
that coming from different individuals or
groups at a single point in time
Time series data usually follows one
subject's changes over the course of time.
Cross-sectional data refers to data
collected by observing many subjects
(such as individuals, firms or
countries/regions) at the same point of
time.
It focuses on results gained over an
extended period of time, often within a
small area
It focuses on the information received
from surveys and opinions at a particular
time, in various locations, depending on
the information sought.
Example: The daily closing price of a
certain stock recorded over the last six
weeks is an example of time-series data
Example: The closing prices of a group of
20 different stocks on December 15, 1986
this would be an example of cross-
sectional data

4. Cont…
A study on random sample of 4000 graphics from 15 of the
world’s news papers published between 1974 and 1989
found that more than 75% of all graphics were time series.
Sales figures jan 98 - dec 01
0
5
10
15
20
25
30
35
40
45
jun-97
jan-98
jul-98
feb-99
aug-99
mar-00
okt-00
apr-01
nov-01
maj-02

5. Cont…
Tot-P ug/l, Råån, Helsingborg 1980-2001
0
100
200
300
400
500
600
700
800
900
1000
1980-01-15
1981-01-15
1982-01-15
1983-01-15
1984-01-15
1985-01-15
1986-01-15
1987-01-15
1988-01-15
1989-01-15
1990-01-15
1991-01-15
1992-01-15
1993-01-15
1994-01-15
1995-01-15
1996-01-15
1997-01-15
1998-01-15
1999-01-15
2000-01-15
2001-01-15

6. Cont…
Mathematically,
Ut = f(t)
Ut : Value of the phenomenon or variable under
consideration at time t.
For example, (i) population of a country or region (Ut) in
different year (t)
(ii) Number of births and deaths (Ut) in different months
(t)
(iii) Sales of a store (Ut) in different months (t)
(iv) Temperatures (Ut) of a place in different days (t) etc.

7. Cont…
Time series gives a bi-variate distribution, one
of the variables being time (t) and the other
being the value (Ut)
 Time t may be yearly, monthly, weekly,
daily or even hourly
Usually equal interval

8. Components of a time series
 The pattern or behavior of the data in a time series
has several components.
 Theoretically, any time series can be decomposed
into:
Secular Trend or Long term movement
Periodic change or short term movement
(i) Seasonal (ii) Cyclical
Irregular or random components
 However, this decomposition is often not straight-
forward because these factors interact.

9. Trend component
 The trend component accounts for the gradual shifting of the
time series to relatively higher or lower values over a long
period of time.
 Trend is usually the result of long-term factors such as
changes in the population, demographics, technology, or
consumer preferences.

10. Cont…
 Downward trend: Declining birth or death rate
 Upward trend: Population growth, agricultural
production
 Mathematically trend may be Linear or non-linear
(curvi-linear)
 The term “long time period” is a relative term.

11. Periodic movements
Forces which prevent the smooth flow of
the series in a particular direction and
tend to repeat themselves over a period
of time
Seasonal variations or fluctuations
Cyclical variations or fluctuations

12. Seasonal Variations
The component responsible for the regular rise
or fall (fluctuations) in the time series during a
period not more than 1 year.
Fluctuations occur in regular sequence
(periodical)
The period being a month, a week, a day, or
even a fraction of the day, an hour etc.

13. Cont…

14. Cont…
Time series data depicted annually do not
represent seasonal variations. Seasonal
variations may be attributed to the following
reasons:
1. Natural forces : Weather or seasons
2. Man-made conventions: Habits, Fashions,
Customs or rituals etc.

15. Cyclical Variations
Cycle refers to recurrent variations/oscillatory
movements in time series
Cyclical variations usually last longer than a
year
One complete period is called “Cycle”

16. Cont…
Business Cycle (Four phase Cycle)
ProsPerity (Period of Boom)
recovery recession
dePression

17. Cont…

18. Irregular or Random Variations
Random or irregular or residual fluctuations
Beyond the control of human (unpredictable)
Earthquakes, Wars, Floods, Revolutions etc.
Short duration and non-repeating

19. Cont…

20. Purpose of Time series
 To identify the components, the net effects of
whose interaction is exhibited by the
movement of a time series
 To isolate, study, analyze and measure them
independently i.e; holding the other things
constant

21. Uses of Time Series
To study the past behavior of the variable
To formulate policy decisions and planning of
future operations.
To predict or estimate or forecast the behavior
of the phenomenon in future which is very
essential for business planning
To compare the changes in the values of
different phenomenon at different times

22. Decomposition of Time series
 Decomposition by Additive hypothesis
Ut= Tt + St + Ct + Rt
Ut= Time Series value at time t
Tt = Trend component
St = Seasonal component
Ct = Cyclical component
Rt= Random component

23. Cont…
 Decomposition by Multiplicative hypothesis
Ut= Tt x St x Ct x Rt
= logU˃ t= logTt + logSt + logCt + logRt

24. Measurement of Trend
The following methods are used to measure
“Trend”:
1. Graphic method
2. Method of Semi-Averages
3. Method of Curve fitting by principles of least
squares
4. Method of Moving average